OpenGL 绘图实例五之平移缩放旋转

综述

OpenGL 中的变换可以分为下面的三种：即模型变换、投影变换、视口变换。模型变换其实就相当于图形的几何变换，包括平移、缩放、旋转等操作，下面我们来详细研究一下 OpenGL 中三种操作的函数应用。

准备工作

在变换前我们首先要做一下准备工作，首先我们需要调用 glMatrixMode 函数来设置变换模式。该方法介绍如下 glMatrixMode(Glenum mode)，设置当前矩阵模式，它具有三个参数，分别为 GL_MODELVIEW，GL_PROJECTION，GL_TEXTURE。三个参数的含义为：

GL_MODELVIEW, 对模型视景矩阵堆栈应用随后的矩阵操作，也就是针对本节的模型几何变换设置的模式，本节所有内容均为此模式。 GL_PROJECTION, 对投影矩阵应用随后的矩阵操作，在投影变换中设置的模式。 GL_TEXTURE, 对纹理矩阵堆栈应用随后的矩阵操作，在设置动态纹理的过程中设置的模式。

所以，在本节我们就需要设置如下的模式

glMatrixMode(GL_MODELVIEW);

接下来，我们需要设置

glLoadIdentity();

这个方法的作用是设置将当前的用户坐标系的原点移到了屏幕中心，类似于一个复位操作。好，设置好以上两个条件之后我们就可以来进行变换啦。主要有以下三个函数：

glRotatef(angle,vx,vy,vz) //绕向量(vx,vy,vz)为轴旋转角度angle
glTranslate(dx,dy,dz) //平移，位移量为向量(dx,dy,dz)
glScalef(sx,sy,sz) //比例缩放，x，y，z 方向的缩放因子分别为sx，sy，sz

下面我们来详细说明这三个函数的用法。

平移

三种变换中，平移变换是最简单的。类库中提供了下面两个方法：

glTranslated(GLdouble x,GLdouble y,GLdouble z) glTranslatef(GLfloat x,GLfloat y,GLfloat z)

这两种方法是基本是等价的，一种方法是传入 double 类型的参数，另一个是传入 float 类型的参数。方法的作用是将物体分别沿 x，y，z 轴平移 x，y，z 的单位长度。利用上一节的机器人我们来感受一下

1. 向右平移 100 像素

glTranslated(100,0,0);

运行结果可以看到，机器人向右平移了 100 像素

2. 向左下分别平移 50,50 像素

glTranslated(-50,-50,0);

运行结果可以看到，机器人分别向左和向下平移了 50 像素

3. 向左下分别平移 50,50，向前平移 100

glTranslated(-50,-50,100);

运行结果哦，和上一个类似，也就是说在 z 轴上平移没有什么效果吗？难道因为我画的是二维平面图形？哦不，那不应该是距离我的视线更近了所以看到的更大了吗？好吧，事实好像不是这样的，我就姑且认为二维平面在 z 轴上的平移是没有影响的吧。恩，这个函数基本用法就是这样，通过传入不同的 x，y，z 值实现平移即可。

旋转

旋转的方法有下面两个：

glRotatef(GLdouble angle,GLdouble x,GLdouble y,GLdouble z) glRotatef(GLfloat angle,GLfloat x,GLfloat y,GLfloat z)

其中第一个参数是旋转的角度，后面三个参数 x,yz 参数确立了旋转轴，旋转轴是原点 (0,0,0) 与 (x,y,z) 的连线。下面我们用几个例子来感受一下

1. 绕 x 轴旋转 60 度

glRotated(60,10,0,0);

运行结果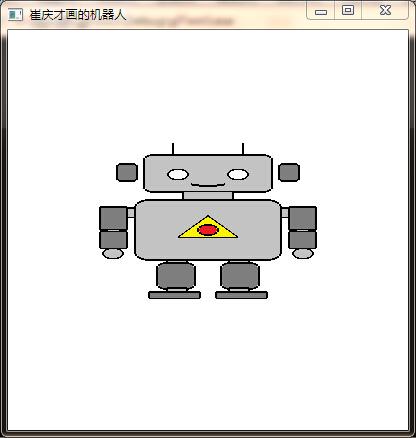恩，它变扁了，旋转中心在机器人的中心，也就是中间的小红点，设想一下，绕 x 轴旋转 60 度，的确我们看到的应该就是变扁的机器人

2. 绕 z 轴旋转 90 度

glRotated(90,0,0,10);

可以看到，机器人绕中心点旋转了 90 度，是逆时针方向。

3. 旋转平移结合

感受完上面的两个例子之后，重头戏来了，上面的例子中旋转轴是 (0,0,0) 和 (x,y,z) 两点的连线，也就是旋转轴总是通过坐标原点的。那如果我们要让物体绕特定的旋转轴来旋转，比如绕 (1,2,3) 和 (4,5,6) 来旋转怎么办？这里就要用到平移和旋转的组合了。

如果旋转轴通过 (xp,yp,zp)，而不通过坐标原点。假如旋转轴为 (xp,yp,zp) 和 (xq,yq,zq) 确立的。我们首先要将图形沿 x,y,z 方向分别平移 – xp,-yp,-zp，然后旋转参数 (x,y,z) 分别传入 (xq-xp,yq-yp,zq-zp) 三个值，旋转完毕之后再把图形沿 x,y,z 方向分别平移 xp,yp,zp 个单位长度即可。

在这里，我的教材和指导书中的内容又发生了冲突，教材中说的是先沿 x,y,z 方向分别平移 -xp,-yp,-zp，再沿 x,y,z 方向分别平移 xp,yp,zp 还原。而指导书中则是先沿 x,y,z 方向分别平移 xp,yp,zp，再沿 x,y,z 方向分别平移 -xp,-yp,-zp 还原，到底谁对谁错呢？我们来一个小例子验证一下。如果觉得无聊，可以自行忽略下面小段内容。为了直观地表示，我们统一设 z 坐标为 0，在 xy 平面中观察变换过程。假设我们有一个点 (2,2,0)，旋转的轴我们设为 (1,2,0) 和 (4,5,0) 的连线，那么该点绕轴旋转 180 度之后应该会是 (1,3,0)，从图上可以很直观地看出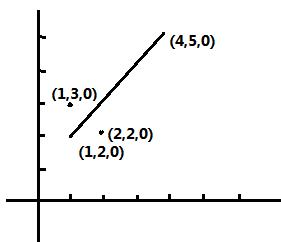那么在调用类库的时候，我们首先就要对这个点进行平移，然后旋转，然后再反平移恢复。

首先，我们按照第一种说法，即先沿 x,y,z 方向分别平移 – xp,-yp,-zp，即 (2,2,0) 减去 (1,2,0)，变为了 (1,0,0)，然后传入 (xq-xp,yq-yp,zq-zp) 实现绕 (0,0,0) 与 (xq-xp,yq-yp,zq-zp) 两点连线为旋转轴来旋转 180 度，显然是绕 (0,0,0) 与 (3,3,0) 的连线来旋转的，这个点变为了 (0,1,0)，然后再沿 x,y,z 方向分别平移 xp,yp,zp 还原，即加 (1,2,0)，即加得到的结果是 (1,3,0)。确实与图中点的符合，所以这一种说法验证正确。另一种说法，即先沿 x,y,z 方向分别平移 xp,yp,zp，即 (2,2,0) 加上 (1,2,0)，变为了 (3,4,0)，然后传入 (xq-xp,yq-yp,zq-zp) 实现绕 (0,0,0) 与 (xq-xp,yq-yp,zq-zp) 两点连线为旋转轴来旋转 180 度，显然是绕 (0,0,0) 与 (3,3,0) 的连线来旋转的，这个点变为了 (4,3,0)，然后再沿 x,y,z 方向分别平移 – xp,-yp,-zp 还原，即减去 (1,2,0)，即加得到的结果是 (3,1,0)。与图中的点不符，所以这一种说法验证失败。

可见，我们得到的结果是

如果旋转轴通过 (xp,yp,zp)，而不通过坐标原点。假如旋转轴为 (xp,yp,zp) 和 (xq,yq,zq) 确立的。我们首先要将图形沿 x,y,z 方向分别平移 – xp,-yp,-zp，然后旋转参数 (x,y,z) 分别传入 (xq-xp,yq-yp,zq-zp) 三个值，旋转完毕之后再把图形沿 x,y,z 方向分别平移 xp,yp,zp 个单位长度即可。

所以，我们要实现机器人绕两点 (10,20,30) 和 (40,50,60) 定义的轴线旋转 45 度，代码实现如下

glTranslatef(-10,-20,-30);
//(40,50,60)-(10,20,30)=(30,30,30)
glRotatef(45,30,30,30);
glTranslatef(10,20,30);

运行结果运行结果可能不太直观，可以直接参考代码实现

缩放

对于缩放，我们的方法也是有两个

glScaled(GLdouble x,GLdouble y,GLdouble z) glScalef(GLfloat x,GLfloat y,GLfloat z)

区别也就是一个参数为 double 类型，一个为 float 类型函数的作用是将物体分别在 x,y,z 轴方向缩放为 x,y,z 倍，缩放中心为原点下面我们来几个小例子感受一下

1. 沿 x 轴放大 2 倍

glScaled(2,1,1);

运行结果画面好美！

2. 沿 y 轴 z 轴分别放大 2 倍

glScaled(1,2,2);

运行结果因为整个图形是一个平面图，所以我们只可以看出 z 轴放缩的效果

3. 放缩和平移的变换

和旋转的原理一样，默认的放缩中心是原点，在这里，如果我们的放缩中心如果不是原点，我们该怎样设置呢？假设放缩中心为 (xp,yp,zp)，方法如下：

如果我们的放缩中心设置为 (xp,yp,zp)，而不是坐标原点。我们首先要将图形沿 x,y,z 方向分别平移 – xp,-yp,-zp，然后放缩参数 (x,y,z) 分别传入三个值代表放缩比例，放缩完毕之后再把图形沿 x,y,z 方向分别平移 xp,yp,zp 个单位长度还原。

下面，我们以 (50,50,50) 为放缩中心来对机器人的 xy 方向分别放缩 1.5 倍

glTranslated(-50,-50,0);
glScaled(1.5,1.5,0);
glTranslated(50,50,0);

运行结果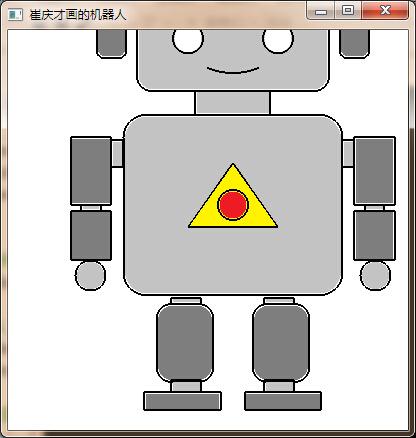这样，我们就实现了以 (50,50,0) 为放缩原点来进行放大 1.5 倍的操作。

综述

在本篇我们描述了 OpenGL 中的平移旋转放缩变换操作，以及一些实例演示，希望对大家有帮助！

来源：https://cuiqingcai.com/1658.html

综述