在上一节中,我们详细讨论了二叉树、AVL平衡二叉树、伸展树、B树和B+树,对树这种重要的数据结构进行了详细的讨论,如果你对数据结构和算法的基本概念还未了解,可以参考:数据结构、算法分析和算法设计。本节主要是对上一节内容的补充,因为上一节中对B树的实现并不好,上一节B树的插入过程如下图:
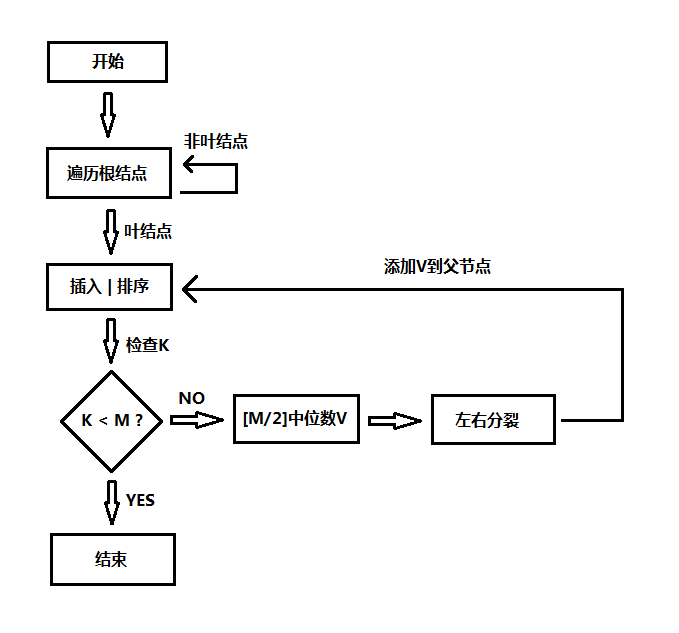
这个算法逻辑实现上是有问题的,因为该算法在向下遍历的插入的时候还往回处理分裂,下面是上节B树的删除大体流程:
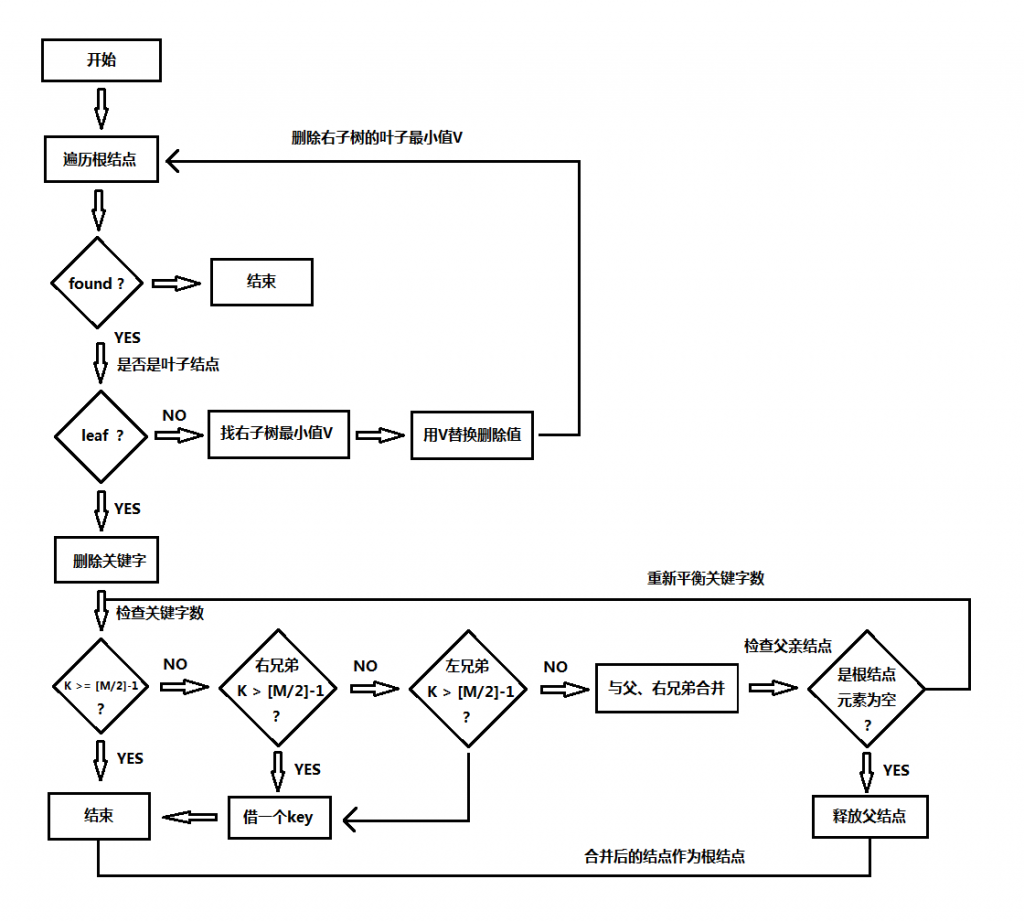
这个算法也是和插入一样类似的问题,在代码实现上会很复杂,大体是没大问题的,有兴趣的朋友可以指出来,下面重新介绍B树和B+树,相关的实现原理和代码实现,对于实现上会采取一种不同的更简单的方式,B+树是B树的扩展,B树可以说是一种广义树,B+树主要应用于大量数据索引的场景,例如操作系统的文件系统和数据库,如MySQL。
一、B树的数据结构和算法详解
1、B树的基本定义
在上一节我们是使用最大度数或阶数M来定义B树的,这种一般的定义方式如下:
- 根结点度数M>=2;
- 叶子结点的深度相同;
- 非叶结点的度数:[M/2] <= T <= M,[]为向上取整符号;
- 结点的关键字数:[M/2]-1 <= K <= M-1;
- 关键字数K和结点度数T的关系为:K=T-1。
以上定义是正确的,但是问题是M如果为奇数在处理插入和删除的时候会有问题,这时候关键字数就为偶数,分裂结点就没那么方便了。
另一种B树的定义是使用最小度数t进行定义,该方式也是算法导论中采取的方式:
- 最小度数t>=2,B树的最小度数与磁盘块的大小有关;
- 根结点的关键字数最小为1;
- 叶子结点的深度相同;
- 非叶非根结点的度数:t <= T <= 2t;
- 非根结点的关键字数:t-1 <= K <= 2t-1;
(6)关键数K和度数的关系为:K = T – 1。
之后你会发现使用最小度数实现B树会更加优雅,B树每个结点的关键字都按升序排列。设B树的关键字数为N,则B树的关键字数N >= 2t^h-1,h为B树的高度h <= log((N+1)/2),底数为t,t>=2,B树的所有一般操作的时间复杂度为O(log N),底数为t。
2、B树的数据结构
B树的结点至少包括:
- 键值数组或关键字数组,长度为2t-1,长度为2t-1时结点为满;
- 最小度数t,最大度数为2t;
- 儿子指针数组,长度为2t;
- 当前关键字数目n,最大值为2t-1;
- 是否是叶子,用于标识一个结点是否是叶子结点,叶子结点没有儿子或其儿子为空。
下面是B树数据结构和算法声明的代码:
//
// Created by Once on 2019/7/22.
//
#ifndef TREE_BTREE_H
#define TREE_BTREE_H
// 键值数组结构
typedef struct column{
int id; // 关键字
char title[128];
} Column;
// B树结点
typedef struct bnode{
int size; // 当前关键字数目
Column **columns; // 键值数组
struct bnode **children; // 儿子指针数组
unsigned int leaf; // 是否为叶子
} BNode;
// B树ADT对外接口
typedef struct btree{
unsigned int degree; // 最小度数
BNode *root; // 根结点
unsigned int size; // B树结点大小
} BTree;
// B树算法操作声明
extern BTree *btree_init(unsigned int degree);
extern int btree_is_full(BTree *btree);
extern int btree_is_empty(BTree *btree);
extern int btree_add(BTree *btree, Column *column);
extern int btree_delete_by_id(BTree *btree, int id);
extern Column *btree_get_by_id(BTree *btree, int id);
extern void btree_traverse(BTree *btree, void(*traverse)(Column*));
extern int btree_clear(BTree *btree);
#endif //TREE_BTREE_H
3、创建B树
C语言使用malloc创建一个B树,可预先创建一个根结点,也可以在插入数据的时候创建,初始化数据结构中的基本值,包括当前关键字数,是否是叶子,在处理B树持久化的时候,需要将新的根结点写入硬盘。这里仅仅初始化B树,不预先创建根结点:
BTree *btree_init(unsigned int degree){
BTree *btree = (BTree*)malloc(sizeof(BTree));
if(!btree){
perror("init b tree error.");
return NULL;
}
btree->root = NULL;
btree->size = 0;
btree->degree = degree;
return btree;
}
4、B树遍历算法
树的遍历原则是以一个关键字为中心,左右儿子为该关键字的上限和下限,在B树遍历中,需要遍历结点上的关键字,在这里可使用while或for循环顺序遍历,时间为O(t),也可以使用二分法遍历,时间为O(log t),顺序遍历一个B树的描述如下,这是一个中序遍历:
- 使用for循环,上限为当前结点关键字数size,索引为i;
- 先遍历第i个非叶子儿子,此时即递归自身;
- 处理第i个关键字;
- 后处理第i+1个儿子,递归自身;
- 处理第i+1个关键字;
- 以上操作循环处理,跳出循环后需要处理最后一个儿子。
B树遍历算法代码如下:
static void traverse_tree(BNode *root, void(*traverse)(Column*)){
int i;
for (i = 0; i < root->size; ++i) {
if(!root->leaf)
traverse_tree(root->children[i], traverse);
traverse(root->columns[i]);
}
if(!root->leaf)
traverse_tree(root->children[i], traverse);
}
void btree_traverse(BTree *btree, void(*traverse)(Column*)){
if(btree == NULL || btree->size == 0)
return;
traverse_tree(btree->root, traverse);
}
5、B树搜索算法
B树的搜索算法输入参数为B树的根结点root和待查找的关键字k,输出为NULL,找到对应的关键字则返回目标结点以及目标关键字的索引位置,这里实现仅仅返回关键字对应的值。
B树搜索的重点在于确定关键字的位置,包括确定相等关键字的位置,同时确定下层儿子的位置,这里要说一下关键字的索引和儿子的索引的关系,如下图:
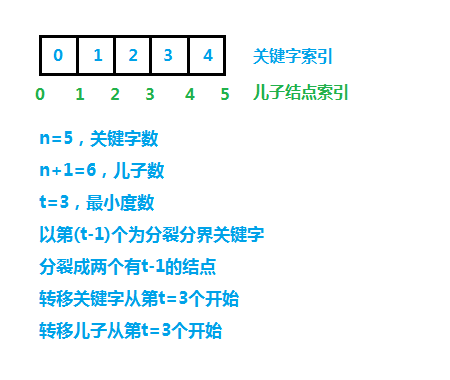
结点上确定关键字位置的算法有两种,线性搜索和二分法搜索,线性搜索的时间为O(t),此时B树的总时间为O(t
log N),底数为t,二分法搜索的时间为O(log t),此时B树的总时间为O(log t log N)),B树搜索算法代码如下:
// 顺序查找结点关键字,每个结点最多关键字为2t-1,时间复杂度为O(2t-1),即O(t)
static int seq_search(const Column *array[], const int len, const int value){
int i = 0;
while(i <= len - 1 && value > array[i]->id)
i++;
return i;
}
// 二分法查找结点上相同的关键字、确定儿子访问位置,每个结点关键字数为2t-1,时间复杂度为O(log(2t-1)),即O(log t)
static int binary_search(Column *array[], const int len, const int value){
int start = 0, end = len - 1, index = 0, center = (start + end) / 2;
while(start <= end){
if(value == array[center]->id){
index = center;
break;
}
else if(value > array[center]->id){
index = center + 1;
center += 1;
start = center;
}
else{
index = center;
center -= 1;
end = center;
}
center = (start + end) / 2;
}
return index;
}
static Column *btree_get(BNode *root, int id){
int index = binary_search(root->columns, root->size, id);
if(index < root->size && root->columns[index]->id == id)
return root->columns[index];
else if(root->leaf)
return NULL;
else
return btree_get(root->children[index], id);
}
Column *btree_get_by_id(BTree *btree, int id){
if(btree == NULL || btree->size == 0)
return NULL;
return btree_get(btree->root, id);
}
6、B树插入算法
B树的插入最主要就是结点分裂了,一般来说如果一个结点满了,则分裂成两个结点,中间的关键字插入到父结点,这样向上分裂,但是关键字是插入到叶子结点的,等到插入关键字再分裂结点,则处理会比较麻烦。
这里B树插入采用另一种方式:插入关键字从根结点自上而下查找关键字所属位置,将关键字添加到叶子结点上;沿途经过的结点若满(满的关键字数为2t-1)则分裂结点,以第(t-1)个关键字为分界点,分成两个结点,每个结点的关键字数为t-1,将第t-1个关键字插入到父结点,这样将关键字插入到叶子结点时就不需要再分裂,如下图,插入6之前先将根结点分裂,然后再从根结点上获取新的路径插入到叶子结点上。
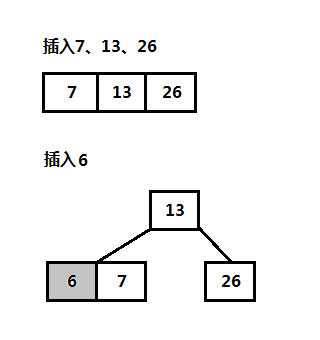
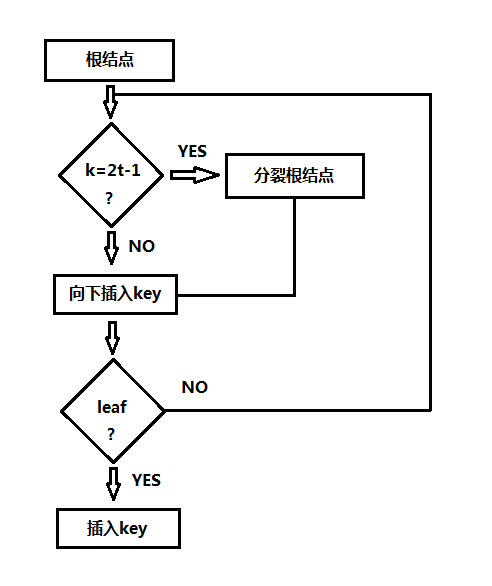
B树插入算法的大体流程如下图所示,其总体流程包括满结点分裂、非满结点插入:
取出根结点,如果根结点已满则分裂该结点,然后更新根结点,向下选择路径,检查途径的结点,如果是内部结点,检查该结点的儿子结点是否已满,若满则分裂,否则继续向下,如果是叶结点则插入关键字,插入结束。
(1)分裂结点算法
分裂结点分裂的不是当前结点,而是当前结点的儿子结点,分裂结点算法的输入参数包含儿子为满的父结点,以及满儿子在父结点中的索引位置i,这个i在向下选择路径的时候可以求得到。
在自上而下查找关键字位置时,分裂途径的满结点,关键字数为2t-1为满,分裂的结点包括叶子结点,这样在分裂当前结点时,可保证它的父结点不是满的,也就是不需要再向上分裂了,分裂算法的详细描述如下:
- 以当前结点作为父结点,检查向下的儿子s结点是否已满,而根结点的分裂会导致创建新的根结点n;
- 如果根结点已满,则创建并初始化新结点n(包括当前关键字数、是否为叶结点),在节点s中将从第t个开始的关键字转移到n中,非叶结点需要从第t个开始转移儿子到n中;
- 将新结点添加到当前结点(父结点)作为儿子;
- 将第t-1个关键字添加到当前结点(父结点)中。
以上分裂算法都是针对当前结点分裂儿子结点,在路径每一个结点上都需要检查,若结点已满则调用该分裂算法,代码如下:
/**
* 1、创建新结点n
* 2、转移关键字到n
* 3、转移儿子到n
* 4、n添加作为parent的儿子
* 5、将中间关键字添加到parent
* */
static int split_child(BTree *btree, BNode *parent, int index){
BNode *left = parent->children[index];
BNode *right = (BNode*)malloc(sizeof(BNode));
if(!right)
return 0;
right->columns = (Column**)malloc(sizeof(Column*) * (2 * btree->degree - 1));
right->children = (BNode**)malloc(sizeof(BNode*) * (2 * btree->degree));
if(!right->columns || !right->children)
return 0;
right->leaf = left->leaf;
for (int i = btree->degree; i < left->size; ++i) {
right->columns[i - btree->degree] = left->columns[i];
}
if(!left->leaf){
for (int i = btree->degree; i < left->size + 1; ++i) {
right->children[i - btree->degree] = left->children[i];
}
}
right->size = btree->degree - 1;
left->size = btree->degree - 1;
for (int k = parent->size; k > index; --k) {
parent->columns[k] = parent->columns[k - 1];
}
parent->columns[index] = left->columns[btree->degree - 1];
for (int j = parent->size + 1; j > index + 1; --j) {
parent->children[j] = parent->children[j - 1];
}
parent->children[index + 1] = right;
parent->size++;
return 1;
}
(2)B树插入关键字
完整的插入算法输入参数包括根结点和待插入的关键字,以上的分裂算法只处理满结点的情况,那么非满结点也需要做处理,下面是该算法的完整描述:
- 先检查B树的根结点,如果根结点为满,则创建一个新的根结点,调用分裂算法进行分裂,处理完成后再以新的根结点为起点调用非满插入算法;
- 关键字数小于2t-1为非满,如果当前结点为叶子结点,则将关键字插入到结点中;
- 如果当前结点为内部结点,获取下一个儿子结点,检查是否需要分裂,分裂完成后,再递归调用非满插入算法。
同样的,以上检查结点是否已满,除了根结点外,都是检查儿子结点的,下面是完整的关键字插入代码:
static int add_none_full(BTree *btree, BNode *root, Column *column){
int index = binary_search(root->columns, root->size, column->id);
if(root->leaf){
if(index < root->size && root->columns[index]->id == column->id){
strcpy(root->columns[index]->title, column->title);
return 1;
}
Column *c = (Column*)malloc(sizeof(Column));
if(!c)
return 0;
c->id = column->id;
strcpy(c->title, column->title);
for (int i = root->size; i > index; --i) {
root->columns[i] = root->columns[i - 1];
}
root->columns[index] = c;
root->size++;
return 1;
}
else{
if(root->children[index]->size == 2*btree->degree - 1){
if(split_child(btree, root, index)){
if(column->id > root->columns[index]->id)
index++;
}
else
return 0;
}
return add_none_full(btree, root->children[index], column);
}
}
static int add_node(BTree *btree, BNode *root, Column *column){
if(!root){
root = new_node(btree);
if(!root)
return 0;
Column *c = (Column*)malloc(sizeof(Column));
if(!c)
return 0;
c->id = column->id;
strcpy(c->title, column->title);
root->leaf = 1;
root->columns[0] = c;
root->size = 1;
btree->root = root;
btree->size++;
return 1;
}
else{
if(root->size == 2*btree->degree - 1){
BNode *node = new_node(btree);
if(!node)
return 0;
node->leaf = 0;
node->size = 0;
btree->root = node;
node->children[0] = root;
btree->size++;
if(split_child(btree, node, 0)){
int i = 0;
if(node->columns[0]->id < column->id)
i++;
return add_none_full(btree, node->children[i], column);
}
return 0;
}
else
return add_none_full(btree, root, column);
}
}
int btree_add(BTree *btree, Column *column){
if(btree == NULL || column == NULL)
return 0;
return add_node(btree, btree->root, column);
}
7、B树删除算法
B树的删除操作比较复杂,下面我们来一步步分析,我们可以想到,删除的情况有两种:内部结点和叶子结点,这里删除的方式也是和插入类似,一次遍历完成删除操作,因为删除一个关键字可能会导致结点关键字不足t-1个,这就需要借或者合并相邻结点。
这里我们采取这样的方式,一般来说非根结点关键字数至少为t-1个(根结点至少为1个关键字),递归下降遍历,对每个沿途经过的结点,保证结点的关键字说为t(比最小关键字数t-1多1),儿子结点关键字不足t时,从父结点下移一个到儿子中,将兄弟结点的关键字上移一个到父结点,当前结点关键字为空,删除当前结点,让儿子成为新的根,这种方式保证内部结点的关键字数至少为t,这样从内部结点删除一个关键字时就不会导致该结点为空或少于t-1个关键字,下图是B树删除操作的大体流程,下面我们详细讨论操作流程:
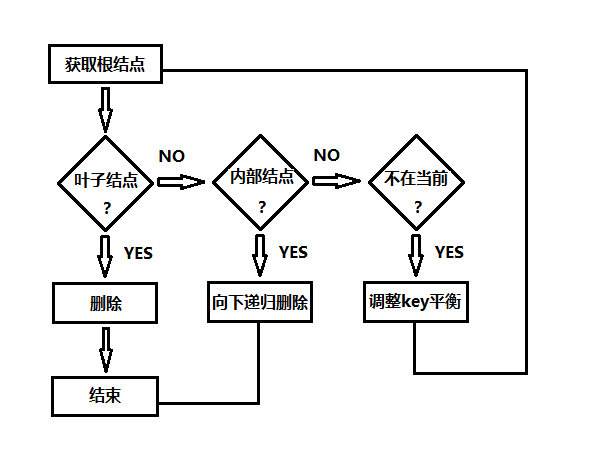
删除操作输入参数为根结点和待删除的关键字k,删除的操作分为以下三种情况:
- k在叶结点中:直接删除关键字k,如果不存在也删除结束;
- k在内部结点中:以当前待删除的关键字k为中心,k有左右儿子:
- k的左儿子关键字数>=t,将左子树的最大值M替换k,递归向下删除M;
- k的右儿子关键字数>=t(k的左儿子的关键字数<t),将右子树的最小值m替换k,递归向下删除m;
- k的左右儿子关键字数==t-1,将k和左右儿子合并进左儿子,在当前结点中释放右儿子和k,从左儿子递归向下删除k。
- k不在当前结点中:当前结点的向下儿子s,k有可能在以s为根的结点中,此时我们需要将s的关键字调整至少t个关键字,(向左借、向右借、合并左或右)调整的情况如下:
- s结点只有t-1个关键字(相邻兄弟关键字>=t),将当前结点的一个关键字下移到s中,将左或右兄弟一个关键字上移到当前结点,将兄弟中关键字相应的儿子移到s结点中;
- s结点和所有相邻兄弟结点都只有t-1个关键字,将s和其中一个兄弟合并,将当前结点的一个关键字移到新合并的结点中。
删除算法可分为:当前结点存在关键字,则删除叶子结点或者内部结点的关键字,不存在则需要检查儿子结点进行填满t个关键字的操作。B树的完整源码可在github上查看:https://github.com/onnple/B-TREE-C,该项目的删除操作有bug,但是由于时间问题就不再进行调试了,感兴趣的朋友可以指正一下。
二、B+树
B+是B树的扩展,它和B树在结构上主要的不同在于,B+树的所有叶结点是使用链表链接的,而且B+树的叶结点包含了全部的关键字,下面B+树图片取自于维基百科:
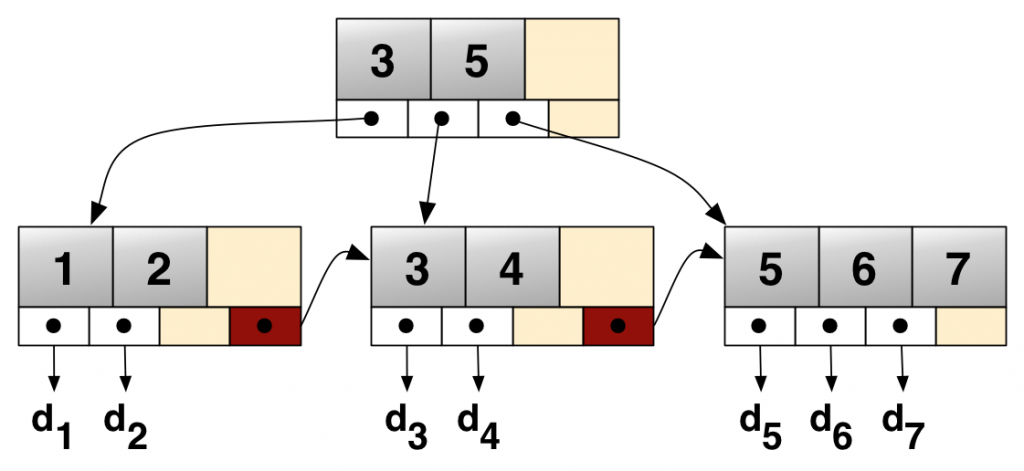
B+树的主要应用在操作系统的文件系统和数据库,这里就不实现B+树了,需要应用B+树的特性那么使用例如MySQL等数据库是最好的方式。
如果需要自定义实现B+树,B+树的数据结构和B树的基本一样,不过叶子结点需要增加左右兄弟的指针。B+树的算法操作也和B树基本一样,但是要注意因为B+树的所有叶子结点包含了所有的关键字,所以在插入操作分裂结点中,中间的关键字除了插入父结点,需要保留在叶子上,删除操作则需要把叶子上相同的关键字一并删除。
三、MySQL数据库索引引擎实现原理
如果你用过MySQL数据库的话,可能知道在MySQL存储数据有几种文件,例如.frm文件、.myi文件、.myd文件和.ibd文件,首先.frm文件是MySQL用于表示表结构的文件,一般创建一个新表都会创建这样的文件。
MySQL数据库有两大索引引擎:MyISAM引擎和InnoDB引擎,这两个索引引擎都是基于B+树实现的,对于MyISAM索引引擎,它是一个非聚簇索引,即在叶子结点上存储数据的地址,所以使用MyISAM索引存储的数据分为两个文件:.myi文件和.myd文件,这两个文件分别存储索引和真实数据。
而对于InnoDB引擎,它直接在叶结点存储数据本身,因此是聚簇索引,只使用一个文件存储索引和真实数据,该文件就是.ibd文件。
1、MySQL索引引擎实现原理
首先我们要清楚,实现MySQL索引引擎并不是直接存储一个B+树,甚至并不需要一个真正的B+树,实际存储的是一个结点的数据,一次IO读取一个结点,从这个结点找出下一个结点的位置再次调用IO读取,所以索引引擎是一个逻辑上的B+树。
为什么要使用B+树索引数据?主要还是因为速度的问题,我们的真实数据存储在磁盘上,一般在内存里面的操作都不算耗时,反而机械磁盘耗时会比较明显,因为磁盘读取有真实的机械性操作,影响磁盘读取速度的主要因素是:盘片的旋转和磁臂的移动。那么如何实现速度最大化呢?那就是B+树了,B+树读取海量的数据只需要O(log
N)次操作,而且其底数t可以最大化,InnoDB是将根结点常驻内存,以一个结点为一个数据单位,一次IO读取一个结点,MySQL设置的一个数据页为16K。
为什么使用B+树而不是B树?要知道B+树的结点不存储任何真实数据,只存储索引数据,而B树是两者都存储,这样相同大小16K的一个结点,B+树存储的索引数据比B树的多很多,这意味着B树的IO操作次数会比B+树的多,所以使用B+树实现索引更有优势,另外一个原因是因为B+树的所有叶结点都是相连的,B+树可以很方便地进行顺序访问或范围性访问。
MySQL在索引引擎实现上并不是严格遵守B+树的定义,例如结点分裂,MySQL采取的原则是空间优先,只要结点空间足够就插入,尽量最大化利用空间。
2、InnoDB存储引擎索引原理
(1)存储结构
A、表空间(table space):一个存储文件的主题,由段组成;
B、段(segment):由簇组成,可分为数据段、索引段和回滚段;
C、区/簇(extent):由64个连续的页空间组成(64x16k),段的最小单位,它是一个连续分配的段空间;
D、页(page):磁盘块的最小单元,16k大小,常见的页有数据页(B-tree Node page)、事务数据页(Transacation system page)、Undo页和系统页,又称为一个记录(page==record),一个页等于一个结点。
(2)数据存储原理
磁盘由盘面、磁头、磁道(Track)、柱面(Cylinder)和扇区(Sector)组成,盘面从上而下从0开始编号,磁头由上而下从0开始编号,磁道由外向内从0开始编号,磁道的一段圆弧叫做扇区,扇区从1开始编号,柱面编号和磁头是一样的。
磁盘的数据寻址有两种方式:逻辑地址和磁盘地址,逻辑地址则是编程代码中获取的数据地址,一般用十六进制表示,磁盘地址是数据的物理地址,一般使用一个三位码表示(柱面号,磁头号,扇区号)。
磁盘IO读写的速度影响因素包括磁盘存储介质和机械运动,上面对索引引擎的存储结构的设计,一个依据是计算机局部性原理,也就是说设计结点的大小需要考虑磁盘块的大小,计算机局部原理是说,当一个数据被使用到时,附近的数据也会被马上用到,程序运行所需数据通常比较集中,在附近柱面,或附近磁头,或附近的扇区,另外程序预读数据也可以提高IO效率,预读的数据长度为页的整数倍。
来源:
https://www.srcmini02.com/1348.html



