RSA算法这是一种非对称密码算法, 这意味着在通信时应涉及两个密钥, 即公钥和私钥。解决RSA算法问题的步骤很简单。
示例1:
步骤1:选择两个质数
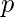
和
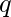
让我们来
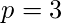
和
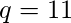
步骤2:计算的值
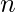
和
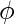
给出为
and在这个例子中
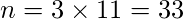
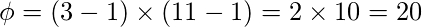
步骤3:找出的值
(公钥)
选择
, 这样
应该是互质的。互素意味着它不应该乘以
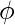
而且不除以
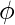
影响因素
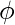
是,
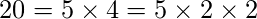
so
不应乘以
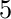
和
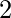
并且不应除以20。
因此, 素数是3、7、11、17、19…, 因为选择了3和11
如7
因此,
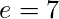
步骤4:计算的值
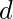
(私钥)
条件为
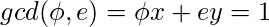
y是
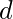
.
计算的值
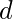
,
形成一个包含四列的表, 即a, b, d和k。
初始化a = 1, b = 0, d =
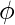
, k = –第一行。
初始化a = 0, b = 1, d =
,
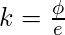
在第二排。
在下一行中, 应用以下公式查找下一个a, b, d和k的值, 其值如下所示:
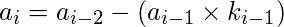
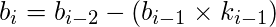
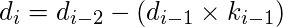
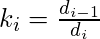
立刻,
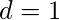
, 请停止该过程并检查以下情况
if
if对于给定的示例, 该表将为
| 一种 | b | d | ķ |
|---|---|---|---|
| 1 | 0 | 20 | – |
| 0 | 1 | 7 | 2 |
| 1 | -2 | 6 | 1 |
| -1 | 3 | 1 | – |
如上表
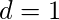
, 请停止该过程并检查为
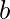
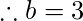
验证
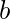
是正确的, 上述条件应满足, 即
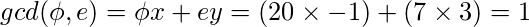
。因此
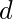
是正确的。
步骤5:进行加密和解密
加密方式为
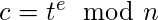
解密为
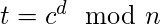
对于给定的示例, 假设
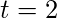
, 所以
加密是
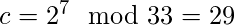
解密为
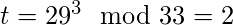
因此, 在最后,
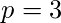
,
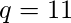
,
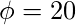
,
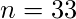
,
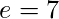
和
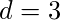
示例2:
GATE CS-2017(Set 1)
在RSA密码系统中, 特定的A使用两个质数p = 13和q = 17生成她的公钥和私钥。如果A的公钥是35。那么A的私钥是?
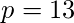
和
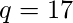
计算
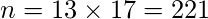
和
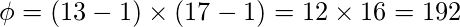
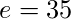
(公钥)
计算
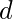
(私钥)
| a | b | d | k |
|---|---|---|---|
| 1 | 0 | 192 | – |
| 0 | 1 | 35 | 5 |
| 1 | -5 | 17 | 2 |
| -2 | 11 | 1 | – |
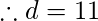
(私钥)
来源:
https://www.srcmini02.com/68763.html



