本文概述
一棵树, 没有叶子比其他叶子离根更远。不同的平衡方案允许对”更远的距离”进行不同的定义, 并进行不同的工作量以保持平衡。
考虑一种高度平衡方案, 其中应检查以下条件以确定二叉树是否平衡。
一棵空树是高度平衡的。如果满足以下条件, 则非空二叉树T是平衡的:
1)T的左子树是平衡的
2)T的右子树是平衡的
3)左子树和右子树的高度之差不大于1。
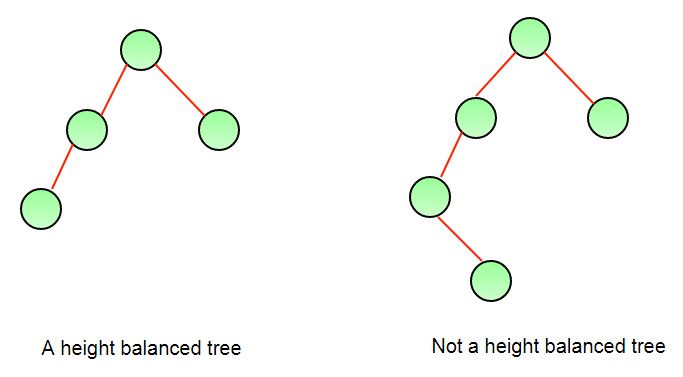
上面的高度平衡方案用于AVL树中。下图显示了两棵树, 其中一棵是高度平衡的, 而另一棵则不是。第二棵树没有高度平衡, 因为左子树的高度比右子树的高度大2。
要检查树是否高度平衡, 请获取左右子树的高度。如果高度差不超过1并且左右子树是平衡的, 则返回true, 否则返回false。
C++
/* CPP program to check if
a tree is height-balanced or not */
#include <bits/stdc++.h>
using namespace std;
/* A binary tree node has data, pointer to left child and
a pointer to right child */
class node {
public :
int data;
node* left;
node* right;
};
/* Returns the height of a binary tree */
int height(node* node);
/* Returns true if binary tree
with root as root is height-balanced */
bool isBalanced(node* root)
{
int lh; /* for height of left subtree */
int rh; /* for height of right subtree */
/* If tree is empty then return true */
if (root == NULL)
return 1;
/* Get the height of left and right sub trees */
lh = height(root->left);
rh = height(root->right);
if ( abs (lh - rh) <= 1 && isBalanced(root->left) && isBalanced(root->right))
return 1;
/* If we reach here then
tree is not height-balanced */
return 0;
}
/* UTILITY FUNCTIONS TO TEST isBalanced() FUNCTION */
/* returns maximum of two integers */
int max( int a, int b)
{
return (a>= b) ? a : b;
}
/* The function Compute the "height"
of a tree. Height is the number of
nodes along the longest path from
the root node down to the farthest leaf node.*/
int height(node* node)
{
/* base case tree is empty */
if (node == NULL)
return 0;
/* If tree is not empty then
height = 1 + max of left
height and right heights */
return 1 + max(height(node->left), height(node->right));
}
/* Helper function that allocates
a new node with the given data
and NULL left and right pointers. */
node* newNode( int data)
{
node* Node = new node();
Node->data = data;
Node->left = NULL;
Node->right = NULL;
return (Node);
}
//Driver code
int main()
{
node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
root->left->left->left = newNode(8);
if (isBalanced(root))
cout <<"Tree is balanced" ;
else
cout <<"Tree is not balanced" ;
return 0;
}
//This code is contributed by rathbhupendraC
/* C program to check if a tree is height-balanced or not */
#include <stdio.h>
#include <stdlib.h>
#define bool int
/* A binary tree node has data, pointer to left child
and a pointer to right child */
struct node {
int data;
struct node* left;
struct node* right;
};
/* Returns the height of a binary tree */
int height( struct node* node);
/* Returns true if binary tree with root as root is height-balanced */
bool isBalanced( struct node* root)
{
int lh; /* for height of left subtree */
int rh; /* for height of right subtree */
/* If tree is empty then return true */
if (root == NULL)
return 1;
/* Get the height of left and right sub trees */
lh = height(root->left);
rh = height(root->right);
if ( abs (lh - rh) <= 1 && isBalanced(root->left) && isBalanced(root->right))
return 1;
/* If we reach here then tree is not height-balanced */
return 0;
}
/* UTILITY FUNCTIONS TO TEST isBalanced() FUNCTION */
/* returns maximum of two integers */
int max( int a, int b)
{
return (a>= b) ? a : b;
}
/* The function Compute the "height" of a tree. Height is the
number of nodes along the longest path from the root node
down to the farthest leaf node.*/
int height( struct node* node)
{
/* base case tree is empty */
if (node == NULL)
return 0;
/* If tree is not empty then height = 1 + max of left
height and right heights */
return 1 + max(height(node->left), height(node->right));
}
/* Helper function that allocates a new node with the
given data and NULL left and right pointers. */
struct node* newNode( int data)
{
struct node* node = ( struct node*)
malloc ( sizeof ( struct node));
node->data = data;
node->left = NULL;
node->right = NULL;
return (node);
}
int main()
{
struct node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
root->left->left->left = newNode(8);
if (isBalanced(root))
printf ( "Tree is balanced" );
else
printf ( "Tree is not balanced" );
getchar ();
return 0;
}Java
/* Java program to determine if binary tree is
height balanced or not */
/* A binary tree node has data, pointer to left child, and a pointer to right child */
class Node {
int data;
Node left, right;
Node( int d)
{
data = d;
left = right = null ;
}
}
class BinaryTree {
Node root;
/* Returns true if binary tree with root as root is height-balanced */
boolean isBalanced(Node node)
{
int lh; /* for height of left subtree */
int rh; /* for height of right subtree */
/* If tree is empty then return true */
if (node == null )
return true ;
/* Get the height of left and right sub trees */
lh = height(node.left);
rh = height(node.right);
if (Math.abs(lh - rh) <= 1
&& isBalanced(node.left)
&& isBalanced(node.right))
return true ;
/* If we reach here then tree is not height-balanced */
return false ;
}
/* UTILITY FUNCTIONS TO TEST isBalanced() FUNCTION */
/* The function Compute the "height" of a tree. Height is the
number of nodes along the longest path from the root node
down to the farthest leaf node.*/
int height(Node node)
{
/* base case tree is empty */
if (node == null )
return 0 ;
/* If tree is not empty then height = 1 + max of left
height and right heights */
return 1 + Math.max(height(node.left), height(node.right));
}
public static void main(String args[])
{
BinaryTree tree = new BinaryTree();
tree.root = new Node( 1 );
tree.root.left = new Node( 2 );
tree.root.right = new Node( 3 );
tree.root.left.left = new Node( 4 );
tree.root.left.right = new Node( 5 );
tree.root.left.left.left = new Node( 8 );
if (tree.isBalanced(tree.root))
System.out.println( "Tree is balanced" );
else
System.out.println( "Tree is not balanced" );
}
}
//This code has been contributed by Mayank Jaiswal(mayank_24)Python3
"""
Python3 program to check if a tree is height-balanced
"""
# A binary tree Node
class Node:
# Constructor to create a new Node
def __init__( self , data):
self .data = data
self .left = None
self .right = None
# function to find height of binary tree
def height(root):
# base condition when binary tree is empty
if root is None :
return 0
return max (height(root.left), height(root.right)) + 1
# function to check if tree is height-balanced or not
def isBalanced(root):
# Base condition
if root is None :
return True
# for left and right subtree height
lh = height(root.left)
rh = height(root.right)
# allowed values for (lh - rh) are 1, -1, 0
if ( abs (lh - rh) <= 1 ) and isBalanced(
root.left) is True and isBalanced( root.right) is True :
return True
# if we reach here means tree is not
# height-balanced tree
return False
# Driver function to test the above function
root = Node( 1 )
root.left = Node( 2 )
root.right = Node( 3 )
root.left.left = Node( 4 )
root.left.right = Node( 5 )
root.left.left.left = Node( 8 )
if isBalanced(root):
print ( "Tree is balanced" )
else :
print ( "Tree is not balanced" )
# This code is contributed by Shweta SinghC#
using System;
/* C# program to determine if binary tree is
height balanced or not */
/* A binary tree node has data, pointer to left child, and a pointer to right child */
public class Node {
public int data;
public Node left, right;
public Node( int d)
{
data = d;
left = right = null ;
}
}
public class BinaryTree {
public Node root;
/* Returns true if binary tree with root as
root is height-balanced */
public virtual bool isBalanced(Node node)
{
int lh; //for height of left subtree
int rh; //for height of right subtree
/* If tree is empty then return true */
if (node == null ) {
return true ;
}
/* Get the height of left and right sub trees */
lh = height(node.left);
rh = height(node.right);
if (Math.Abs(lh - rh) <= 1 && isBalanced(node.left)
&& isBalanced(node.right)) {
return true ;
}
/* If we reach here then tree is not height-balanced */
return false ;
}
/* UTILITY FUNCTIONS TO TEST isBalanced() FUNCTION */
/* The function Compute the "height" of a tree. Height is the
number of nodes along the longest path from the root node
down to the farthest leaf node.*/
public virtual int height(Node node)
{
/* base case tree is empty */
if (node == null ) {
return 0;
}
/* If tree is not empty then height = 1 + max of left
height and right heights */
return 1 + Math.Max(height(node.left), height(node.right));
}
public static void Main( string [] args)
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
tree.root.left.left.left = new Node(8);
if (tree.isBalanced(tree.root)) {
Console.WriteLine( "Tree is balanced" );
}
else {
Console.WriteLine( "Tree is not balanced" );
}
}
}
//This code is contributed by Shrikant13输出如下:
Tree is not balanced时间复杂度:O(n ^ 2)最坏的情况发生在树倾斜的情况下。
优化的实现:
可以通过在相同的递归中计算高度而不是单独调用height()函数来优化上述实现。感谢Amar建议这个优化版本。这种优化将时间复杂度降低到O(n)。
C++
/* C++ program to check if a tree
is height-balanced or not */
#include <bits/stdc++.h>
using namespace std;
#define bool int
/* A binary tree node has data, pointer to left child and
a pointer to right child */
class node {
public :
int data;
node* left;
node* right;
};
/* The function returns true if root is
balanced else false The second parameter
is to store the height of tree. Initially, we need to pass a pointer to a location with
value as 0. We can also write a wrapper
over this function */
bool isBalanced(node* root, int * height)
{
/* lh --> Height of left subtree
rh --> Height of right subtree */
int lh = 0, rh = 0;
/* l will be true if left subtree is balanced
and r will be true if right subtree is balanced */
int l = 0, r = 0;
if (root == NULL) {
*height = 0;
return 1;
}
/* Get the heights of left and right subtrees in lh and rh
And store the returned values in l and r */
l = isBalanced(root->left, &lh);
r = isBalanced(root->right, &rh);
/* Height of current node is max of heights of left and
right subtrees plus 1*/
*height = (lh> rh ? lh : rh) + 1;
/* If difference between heights of left and right
subtrees is more than 2 then this node is not balanced
so return 0 */
if ( abs (lh - rh)>= 2)
return 0;
/* If this node is balanced and left and right subtrees
are balanced then return true */
else
return l && r;
}
/* UTILITY FUNCTIONS TO TEST isBalanced() FUNCTION */
/* Helper function that allocates a new node with the
given data and NULL left and right pointers. */
node* newNode( int data)
{
node* Node = new node();
Node->data = data;
Node->left = NULL;
Node->right = NULL;
return (Node);
}
//Driver code
int main()
{
int height = 0;
/* Constructed binary tree is
1
/\
2 3
/\ /
4 5 6
/
7
*/
node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
root->right->left = newNode(6);
root->left->left->left = newNode(7);
if (isBalanced(root, &height))
cout <<"Tree is balanced" ;
else
cout <<"Tree is not balanced" ;
return 0;
}
//This is code is contributed by rathbhupendraC
/* C program to check if a tree is height-balanced or not */
#include <stdio.h>
#include <stdlib.h>
#define bool int
/* A binary tree node has data, pointer to left child
and a pointer to right child */
struct node {
int data;
struct node* left;
struct node* right;
};
/* The function returns true if root is balanced else false
The second parameter is to store the height of tree.
Initially, we need to pass a pointer to a location with value
as 0. We can also write a wrapper over this function */
bool isBalanced( struct node* root, int * height)
{
/* lh --> Height of left subtree
rh --> Height of right subtree */
int lh = 0, rh = 0;
/* l will be true if left subtree is balanced
and r will be true if right subtree is balanced */
int l = 0, r = 0;
if (root == NULL) {
*height = 0;
return 1;
}
/* Get the heights of left and right subtrees in lh and rh
And store the returned values in l and r */
l = isBalanced(root->left, &lh);
r = isBalanced(root->right, &rh);
/* Height of current node is max of heights of left and
right subtrees plus 1*/
*height = (lh> rh ? lh : rh) + 1;
/* If difference between heights of left and right
subtrees is more than 2 then this node is not balanced
so return 0 */
if ( abs (lh - rh)>= 2)
return 0;
/* If this node is balanced and left and right subtrees
are balanced then return true */
else
return l && r;
}
/* UTILITY FUNCTIONS TO TEST isBalanced() FUNCTION */
/* Helper function that allocates a new node with the
given data and NULL left and right pointers. */
struct node* newNode( int data)
{
struct node* node = ( struct node*)
malloc ( sizeof ( struct node));
node->data = data;
node->left = NULL;
node->right = NULL;
return (node);
}
//Driver code
int main()
{
int height = 0;
/* Constructed binary tree is
1
/ \
2 3
/ \ /
4 5 6
/
7
*/
struct node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
root->right->left = newNode(6);
root->left->left->left = newNode(7);
if (isBalanced(root, &height))
printf ( "Tree is balanced" );
else
printf ( "Tree is not balanced" );
getchar ();
return 0;
}Java
/* Java program to determine if binary tree is
height balanced or not */
/* A binary tree node has data, pointer to left child, and a pointer to right child */
class Node {
int data;
Node left, right;
Node( int d)
{
data = d;
left = right = null ;
}
}
//A wrapper class used to modify height across
//recursive calls.
class Height {
int height = 0 ;
}
class BinaryTree {
Node root;
/* Returns true if binary tree with root as root is height-balanced */
boolean isBalanced(Node root, Height height)
{
/* If tree is empty then return true */
if (root == null ) {
height.height = 0 ;
return true ;
}
/* Get heights of left and right sub trees */
Height lheight = new Height(), rheight = new Height();
boolean l = isBalanced(root.left, lheight);
boolean r = isBalanced(root.right, rheight);
int lh = lheight.height, rh = rheight.height;
/* Height of current node is max of heights of
left and right subtrees plus 1*/
height.height = (lh> rh ? lh : rh) + 1 ;
/* If difference between heights of left and right
subtrees is more than 2 then this node is not balanced
so return 0 */
if (Math.abs(lh - rh)>= 2 )
return false ;
/* If this node is balanced and left and right subtrees
are balanced then return true */
else
return l && r;
}
public static void main(String args[])
{
Height height = new Height();
/* Constructed binary tree is
1
/ \
2 3
/ \ /
4 5 6
/
7 */
BinaryTree tree = new BinaryTree();
tree.root = new Node( 1 );
tree.root.left = new Node( 2 );
tree.root.right = new Node( 3 );
tree.root.left.left = new Node( 4 );
tree.root.left.right = new Node( 5 );
tree.root.right.right = new Node( 6 );
tree.root.left.left.left = new Node( 7 );
if (tree.isBalanced(tree.root, height))
System.out.println( "Tree is balanced" );
else
System.out.println( "Tree is not balanced" );
}
}
//This code has been contributed by Mayank Jaiswal(mayank_24)Python3
"""
Python3 program to check if Binary tree is
height-balanced
"""
# A binary tree node
class Node:
# constructor to create node of
# binary tree
def __init__( self , data):
self .data = data
self .left = self .right = None
# utility class to pass height object
class Height:
def __init__( self ):
self .height = 0
# helper function to check if binary
# tree is height balanced
def isBalanced(root):
# lh and rh to store height of
# left and right subtree
lh = Height()
rh = Height()
# Base condition when tree is
# empty return true
if root is None :
return True
# l and r are used to check if left
# and right subtree are balanced
l = isBalanced(root.left)
r = isBalanced(root.right)
# height of tree is maximum of
# left subtree height and
# right subtree height plus 1
if abs (lh.height - rh.height) <= 1 :
return l and r
# if we reach here then the tree
# is not balanced
return False
# Driver function to test the above function
"""
Constructed binary tree is
1
/\
2 3
/\ /
4 5 6 /7
"""
# to store the height of tree during traversal
root = Node( 1 )
root.left = Node( 2 )
root.right = Node( 3 )
root.left.left = Node( 4 )
root.left.right = Node( 5 )
root.right.left = Node( 6 )
root.left.left.left = Node( 7 )
if isBalanced(root):
print ( 'Tree is balanced' )
else :
print ( 'Tree is not balanced' )
# This code is contributed by Shweta SinghC#
using System;
/* C# program to determine if binary tree is
height balanced or not */
/* A binary tree node has data, pointer to left child, and a pointer to right child */
public class Node {
public int data;
public Node left, right;
public Node( int d)
{
data = d;
left = right = null ;
}
}
//A wrapper class used to modify height across
//recursive calls.
public class Height {
public int height = 0;
}
public class BinaryTree {
public Node root;
/* Returns true if binary tree with root as root is height-balanced */
public virtual bool isBalanced(Node root, Height height)
{
/* If tree is empty then return true */
if (root == null ) {
height.height = 0;
return true ;
}
/* Get heights of left and right sub trees */
Height lheight = new Height(), rheight = new Height();
bool l = isBalanced(root.left, lheight);
bool r = isBalanced(root.right, rheight);
int lh = lheight.height, rh = rheight.height;
/* Height of current node is max of heights of
left and right subtrees plus 1*/
height.height = (lh> rh ? lh : rh) + 1;
/* If difference between heights of left and right
subtrees is more than 2 then this node is not balanced
so return 0 */
if (Math.Abs(lh - rh)>= 2) {
return false ;
}
/* If this node is balanced and left and right subtrees
are balanced then return true */
else {
return l && r;
}
}
/* The function Compute the "height" of a tree. Height is the
number of nodes along the longest path from the root node
down to the farthest leaf node.*/
public virtual int height(Node node)
{
/* base case tree is empty */
if (node == null ) {
return 0;
}
/* If tree is not empty then height = 1 + max of left
height and right heights */
return 1 + Math.Max(height(node.left), height(node.right));
}
public static void Main( string [] args)
{
Height height = new Height();
/* Constructed binary tree is
1
/ \
2 3
/ \ /
4 5 6
/
7 */
BinaryTree tree = new BinaryTree();
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
tree.root.right.right = new Node(6);
tree.root.left.left.left = new Node(7);
if (tree.isBalanced(tree.root, height)) {
Console.WriteLine( "Tree is balanced" );
}
else {
Console.WriteLine( "Tree is not balanced" );
}
}
}
//This code is contributed by Shrikant13输出如下
Tree is balanced时间复杂度:O(n)
如果你发现上述任何代码/算法不正确, 或者找到其他解决相同问题的方法, 请写评论。
来源:
https://www.srcmini02.com/68548.html



