本文概述
给定多边形和点”p”, 请确定”p”是否位于多边形内。边界上的点被视为内部。
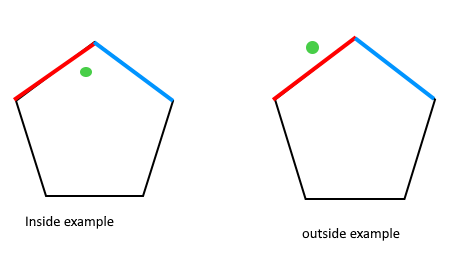
强烈建议你先阅读以下文章。
如何检查两个给定的线段是否相交?
以下是检查点是在内部还是外部的简单想法。
1) Draw a horizontal line to the right of each point and extend it to infinity
1) Count the number of times the line intersects with polygon edges.
2) A point is inside the polygon if either count of intersections is odd or
point lies on an edge of polygon. If none of the conditions is true, then
point lies outside.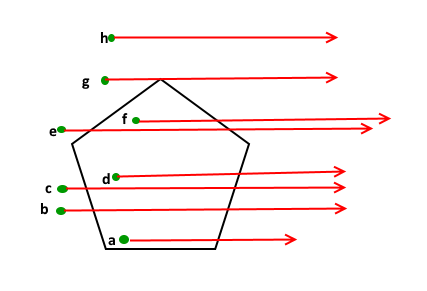
上图中的”g”点如何处理?
注意, 如果该点位于直线上或与给定多边形的顶点之一相同, 则应返回true。为此, 在检查从” p”到极端的线是否相交后, 我们检查” p”是否与当前多边形的线共线。如果是大肠菌, 则我们检查点” p”是否位于多边形的当前侧, 如果位于, 则返回true, 否则返回false。
以下是检查给定点位于多边形内部还是外部的实现。
C++
// A C++ program to check if a given point lies inside a given polygon
// Refer https://www.srcmini.org/check-if-two-given-line-segments-intersect/
// for explanation of functions onSegment(), orientation() and doIntersect()
#include <iostream>
using namespace std;
// Define Infinite (Using INT_MAX caused overflow problems)
#define INF 10000
struct Point
{
int x;
int y;
};
// Given three colinear points p, q, r, the function checks if
// point q lies on line segment 'pr'
bool onSegment(Point p, Point q, Point r)
{
if (q.x <= max(p.x, r.x) && q.x >= min(p.x, r.x) &&
q.y <= max(p.y, r.y) && q.y >= min(p.y, r.y))
return true ;
return false ;
}
// To find orientation of ordered triplet (p, q, r).
// The function returns following values
// 0 --> p, q and r are colinear
// 1 --> Clockwise
// 2 --> Counterclockwise
int orientation(Point p, Point q, Point r)
{
int val = (q.y - p.y) * (r.x - q.x) -
(q.x - p.x) * (r.y - q.y);
if (val == 0) return 0; // colinear
return (val > 0)? 1: 2; // clock or counterclock wise
}
// The function that returns true if line segment 'p1q1'
// and 'p2q2' intersect.
bool doIntersect(Point p1, Point q1, Point p2, Point q2)
{
// Find the four orientations needed for general and
// special cases
int o1 = orientation(p1, q1, p2);
int o2 = orientation(p1, q1, q2);
int o3 = orientation(p2, q2, p1);
int o4 = orientation(p2, q2, q1);
// General case
if (o1 != o2 && o3 != o4)
return true ;
// Special Cases
// p1, q1 and p2 are colinear and p2 lies on segment p1q1
if (o1 == 0 && onSegment(p1, p2, q1)) return true ;
// p1, q1 and p2 are colinear and q2 lies on segment p1q1
if (o2 == 0 && onSegment(p1, q2, q1)) return true ;
// p2, q2 and p1 are colinear and p1 lies on segment p2q2
if (o3 == 0 && onSegment(p2, p1, q2)) return true ;
// p2, q2 and q1 are colinear and q1 lies on segment p2q2
if (o4 == 0 && onSegment(p2, q1, q2)) return true ;
return false ; // Doesn't fall in any of the above cases
}
// Returns true if the point p lies inside the polygon[] with n vertices
bool isInside(Point polygon[], int n, Point p)
{
// There must be at least 3 vertices in polygon[]
if (n < 3) return false ;
// Create a point for line segment from p to infinite
Point extreme = {INF, p.y};
// Count intersections of the above line with sides of polygon
int count = 0, i = 0;
do
{
int next = (i+1)%n;
// Check if the line segment from 'p' to 'extreme' intersects
// with the line segment from 'polygon[i]' to 'polygon[next]'
if (doIntersect(polygon[i], polygon[next], p, extreme))
{
// If the point 'p' is colinear with line segment 'i-next', // then check if it lies on segment. If it lies, return true, // otherwise false
if (orientation(polygon[i], p, polygon[next]) == 0)
return onSegment(polygon[i], p, polygon[next]);
count++;
}
i = next;
} while (i != 0);
// Return true if count is odd, false otherwise
return count&1; // Same as (count%2 == 1)
}
// Driver program to test above functions
int main()
{
Point polygon1[] = {{0, 0}, {10, 0}, {10, 10}, {0, 10}};
int n = sizeof (polygon1)/ sizeof (polygon1[0]);
Point p = {20, 20};
isInside(polygon1, n, p)? cout << "Yes \n" : cout << "No \n" ;
p = {5, 5};
isInside(polygon1, n, p)? cout << "Yes \n" : cout << "No \n" ;
Point polygon2[] = {{0, 0}, {5, 5}, {5, 0}};
p = {3, 3};
n = sizeof (polygon2)/ sizeof (polygon2[0]);
isInside(polygon2, n, p)? cout << "Yes \n" : cout << "No \n" ;
p = {5, 1};
isInside(polygon2, n, p)? cout << "Yes \n" : cout << "No \n" ;
p = {8, 1};
isInside(polygon2, n, p)? cout << "Yes \n" : cout << "No \n" ;
Point polygon3[] = {{0, 0}, {10, 0}, {10, 10}, {0, 10}};
p = {-1, 10};
n = sizeof (polygon3)/ sizeof (polygon3[0]);
isInside(polygon3, n, p)? cout << "Yes \n" : cout << "No \n" ;
return 0;
}Java
// A Java program to check if a given point
// lies inside a given polygon
// Refer https://www.srcmini.org/check-if-two-given-line-segments-intersect/
// for explanation of functions onSegment(), // orientation() and doIntersect()
class GFG
{
// Define Infinite (Using INT_MAX
// caused overflow problems)
static int INF = 10000 ;
static class Point
{
int x;
int y;
public Point( int x, int y)
{
this .x = x;
this .y = y;
}
};
// Given three colinear points p, q, r, // the function checks if point q lies
// on line segment 'pr'
static boolean onSegment(Point p, Point q, Point r)
{
if (q.x <= Math.max(p.x, r.x) &&
q.x >= Math.min(p.x, r.x) &&
q.y <= Math.max(p.y, r.y) &&
q.y >= Math.min(p.y, r.y))
{
return true ;
}
return false ;
}
// To find orientation of ordered triplet (p, q, r).
// The function returns following values
// 0 --> p, q and r are colinear
// 1 --> Clockwise
// 2 --> Counterclockwise
static int orientation(Point p, Point q, Point r)
{
int val = (q.y - p.y) * (r.x - q.x)
- (q.x - p.x) * (r.y - q.y);
if (val == 0 )
{
return 0 ; // colinear
}
return (val > 0 ) ? 1 : 2 ; // clock or counterclock wise
}
// The function that returns true if
// line segment 'p1q1' and 'p2q2' intersect.
static boolean doIntersect(Point p1, Point q1, Point p2, Point q2)
{
// Find the four orientations needed for
// general and special cases
int o1 = orientation(p1, q1, p2);
int o2 = orientation(p1, q1, q2);
int o3 = orientation(p2, q2, p1);
int o4 = orientation(p2, q2, q1);
// General case
if (o1 != o2 && o3 != o4)
{
return true ;
}
// Special Cases
// p1, q1 and p2 are colinear and
// p2 lies on segment p1q1
if (o1 == 0 && onSegment(p1, p2, q1))
{
return true ;
}
// p1, q1 and p2 are colinear and
// q2 lies on segment p1q1
if (o2 == 0 && onSegment(p1, q2, q1))
{
return true ;
}
// p2, q2 and p1 are colinear and
// p1 lies on segment p2q2
if (o3 == 0 && onSegment(p2, p1, q2))
{
return true ;
}
// p2, q2 and q1 are colinear and
// q1 lies on segment p2q2
if (o4 == 0 && onSegment(p2, q1, q2))
{
return true ;
}
// Doesn't fall in any of the above cases
return false ;
}
// Returns true if the point p lies
// inside the polygon[] with n vertices
static boolean isInside(Point polygon[], int n, Point p)
{
// There must be at least 3 vertices in polygon[]
if (n < 3 )
{
return false ;
}
// Create a point for line segment from p to infinite
Point extreme = new Point(INF, p.y);
// Count intersections of the above line
// with sides of polygon
int count = 0 , i = 0 ;
do
{
int next = (i + 1 ) % n;
// Check if the line segment from 'p' to
// 'extreme' intersects with the line
// segment from 'polygon[i]' to 'polygon[next]'
if (doIntersect(polygon[i], polygon[next], p, extreme))
{
// If the point 'p' is colinear with line
// segment 'i-next', then check if it lies
// on segment. If it lies, return true, otherwise false
if (orientation(polygon[i], p, polygon[next]) == 0 )
{
return onSegment(polygon[i], p, polygon[next]);
}
count++;
}
i = next;
} while (i != 0 );
// Return true if count is odd, false otherwise
return (count % 2 == 1 ); // Same as (count%2 == 1)
}
// Driver Code
public static void main(String[] args)
{
Point polygon1[] = { new Point( 0 , 0 ), new Point( 10 , 0 ), new Point( 10 , 10 ), new Point( 0 , 10 )};
int n = polygon1.length;
Point p = new Point( 20 , 20 );
if (isInside(polygon1, n, p))
{
System.out.println( "Yes" );
}
else
{
System.out.println( "No" );
}
p = new Point( 5 , 5 );
if (isInside(polygon1, n, p))
{
System.out.println( "Yes" );
}
else
{
System.out.println( "No" );
}
Point polygon2[] = { new Point( 0 , 0 ), new Point( 5 , 5 ), new Point( 5 , 0 )};
p = new Point( 3 , 3 );
n = polygon2.length;
if (isInside(polygon2, n, p))
{
System.out.println( "Yes" );
}
else
{
System.out.println( "No" );
}
p = new Point( 5 , 1 );
if (isInside(polygon2, n, p))
{
System.out.println( "Yes" );
}
else
{
System.out.println( "No" );
}
p = new Point( 8 , 1 );
if (isInside(polygon2, n, p))
{
System.out.println( "Yes" );
}
else
{
System.out.println( "No" );
}
Point polygon3[] = { new Point( 0 , 0 ), new Point( 10 , 0 ), new Point( 10 , 10 ), new Point( 0 , 10 )};
p = new Point(- 1 , 10 );
n = polygon3.length;
if (isInside(polygon3, n, p))
{
System.out.println( "Yes" );
}
else
{
System.out.println( "No" );
}
}
}
// This code is contributed by 29AjayKumarC#
// A C# program to check if a given point
// lies inside a given polygon
// Refer https://www.srcmini.org/check-if-two-given-line-segments-intersect/
// for explanation of functions onSegment(), // orientation() and doIntersect()
using System;
class GFG
{
// Define Infinite (Using INT_MAX
// caused overflow problems)
static int INF = 10000;
class Point
{
public int x;
public int y;
public Point( int x, int y)
{
this .x = x;
this .y = y;
}
};
// Given three colinear points p, q, r, // the function checks if point q lies
// on line segment 'pr'
static bool onSegment(Point p, Point q, Point r)
{
if (q.x <= Math.Max(p.x, r.x) &&
q.x >= Math.Min(p.x, r.x) &&
q.y <= Math.Max(p.y, r.y) &&
q.y >= Math.Min(p.y, r.y))
{
return true ;
}
return false ;
}
// To find orientation of ordered triplet (p, q, r).
// The function returns following values
// 0 --> p, q and r are colinear
// 1 --> Clockwise
// 2 --> Counterclockwise
static int orientation(Point p, Point q, Point r)
{
int val = (q.y - p.y) * (r.x - q.x) -
(q.x - p.x) * (r.y - q.y);
if (val == 0)
{
return 0; // colinear
}
return (val > 0) ? 1 : 2; // clock or counterclock wise
}
// The function that returns true if
// line segment 'p1q1' and 'p2q2' intersect.
static bool doIntersect(Point p1, Point q1, Point p2, Point q2)
{
// Find the four orientations needed for
// general and special cases
int o1 = orientation(p1, q1, p2);
int o2 = orientation(p1, q1, q2);
int o3 = orientation(p2, q2, p1);
int o4 = orientation(p2, q2, q1);
// General case
if (o1 != o2 && o3 != o4)
{
return true ;
}
// Special Cases
// p1, q1 and p2 are colinear and
// p2 lies on segment p1q1
if (o1 == 0 && onSegment(p1, p2, q1))
{
return true ;
}
// p1, q1 and p2 are colinear and
// q2 lies on segment p1q1
if (o2 == 0 && onSegment(p1, q2, q1))
{
return true ;
}
// p2, q2 and p1 are colinear and
// p1 lies on segment p2q2
if (o3 == 0 && onSegment(p2, p1, q2))
{
return true ;
}
// p2, q2 and q1 are colinear and
// q1 lies on segment p2q2
if (o4 == 0 && onSegment(p2, q1, q2))
{
return true ;
}
// Doesn't fall in any of the above cases
return false ;
}
// Returns true if the point p lies
// inside the polygon[] with n vertices
static bool isInside(Point []polygon, int n, Point p)
{
// There must be at least 3 vertices in polygon[]
if (n < 3)
{
return false ;
}
// Create a point for line segment from p to infinite
Point extreme = new Point(INF, p.y);
// Count intersections of the above line
// with sides of polygon
int count = 0, i = 0;
do
{
int next = (i + 1) % n;
// Check if the line segment from 'p' to
// 'extreme' intersects with the line
// segment from 'polygon[i]' to 'polygon[next]'
if (doIntersect(polygon[i], polygon[next], p, extreme))
{
// If the point 'p' is colinear with line
// segment 'i-next', then check if it lies
// on segment. If it lies, return true, otherwise false
if (orientation(polygon[i], p, polygon[next]) == 0)
{
return onSegment(polygon[i], p, polygon[next]);
}
count++;
}
i = next;
} while (i != 0);
// Return true if count is odd, false otherwise
return (count % 2 == 1); // Same as (count%2 == 1)
}
// Driver Code
public static void Main(String[] args)
{
Point []polygon1 = { new Point(0, 0), new Point(10, 0), new Point(10, 10), new Point(0, 10)};
int n = polygon1.Length;
Point p = new Point(20, 20);
if (isInside(polygon1, n, p))
{
Console.WriteLine( "Yes" );
}
else
{
Console.WriteLine( "No" );
}
p = new Point(5, 5);
if (isInside(polygon1, n, p))
{
Console.WriteLine( "Yes" );
}
else
{
Console.WriteLine( "No" );
}
Point []polygon2 = { new Point(0, 0), new Point(5, 5), new Point(5, 0)};
p = new Point(3, 3);
n = polygon2.Length;
if (isInside(polygon2, n, p))
{
Console.WriteLine( "Yes" );
}
else
{
Console.WriteLine( "No" );
}
p = new Point(5, 1);
if (isInside(polygon2, n, p))
{
Console.WriteLine( "Yes" );
}
else
{
Console.WriteLine( "No" );
}
p = new Point(8, 1);
if (isInside(polygon2, n, p))
{
Console.WriteLine( "Yes" );
}
else
{
Console.WriteLine( "No" );
}
Point []polygon3 = { new Point(0, 0), new Point(10, 0), new Point(10, 10), new Point(0, 10)};
p = new Point(-1, 10);
n = polygon3.Length;
if (isInside(polygon3, n, p))
{
Console.WriteLine( "Yes" );
}
else
{
Console.WriteLine( "No" );
}
}
}
// This code is contributed by 29AjayKumar输出如下:
No
Yes
Yes
Yes
No
No时间复杂度:O(n)其中n是给定多边形中的顶点数。
资源:
http://www.dcs.gla.ac.uk/~pat/52233/slides/Geometry1x1.pdf
以上就是检查给定点位于多边形内部还是外部的详细解决代码,如果发现任何不正确的地方, 或者想分享有关上述主题的更多信息, 请发表评论。
来源:
https://www.srcmini02.com/68440.html