R中的马尔可夫链分析

本文概述

什么是马尔可夫链？
什么是吸收马尔可夫链？
销售速度分析
总结

什么是马尔可夫链？

马尔可夫链是一个数学系统, 它根据给定的概率规则经历从一种状态到另一种状态的转变。马尔可夫链是随机过程, 但是它们的区别在于它们必须缺少任何”内存”。即, 系统下一个状态的概率仅取决于系统的当前状态, 而不取决于任何先前的状态。这称为Markov属性(如下所示)：

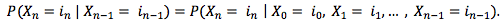
为了具有功能马尔可夫链模型, 必须定义一个转移矩阵Pt。转换矩阵包含有关系统中不同状态之间转换概率的信息。为了使转换矩阵有效, 每一行都必须是一个概率向量, 并且其所有项的总和必须为1。

转换矩阵具有以下特性：后续矩阵的乘积可以描述沿时间间隔的转换概率。因此, 可以通过计算以下步骤来模拟经过k个步骤后处于某种状态的可能性：

本教程还将介绍吸收马尔可夫链。当至少存在一个状态, 一旦达到该状态, 停留在该状态的概率为1(你不能离开它)时, 就会发生这些链。

什么是吸收马尔可夫链？

吸收马尔可夫链是一个马尔可夫链, 其中一旦进入就无法离开某些状态。但是, 这只是马尔可夫链成为吸收性马尔可夫链的前提之一。为了使其成为吸收马尔可夫链, 所有其他瞬态必须能够以1的概率达到吸收状态。

吸收性马尔可夫链具有特定的独特属性, 可将它们与正常的时间均质马尔可夫链区分开。这些属性之一是可以写入过渡矩阵的方式。对于具有t个瞬态和r个吸收态的链, 过渡矩阵P可以按以下规范形式编写：

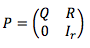
其中Q是t x t矩阵, R是t x r矩阵, 0是r x t零矩阵, Ir是r x r单位矩阵。特别地, 将过渡矩阵分解成基本矩阵允许进行某些计算, 例如直到从每个状态吸收为止的预期步数。基本矩阵N的计算如下：

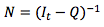
它是一个t x t单位矩阵

预期步骤数基于预期线性度的概念, 其计算公式如下：

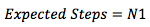
其中1是长度与瞬态数相同且所有条目均为1的列向量

此外, 我们可以计算从任何给定的瞬态开始时被特定吸收状态吸收的概率。此概率计算如下：

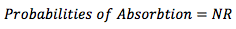
销售速度分析

马尔可夫链广泛用于金融, 博弈论和遗传学等许多领域。但是, 本教程的基础是如何使用它们来建模公司销售过程的时长, 因为这可能是马尔可夫过程。实际上, 这是通过测试序列是否详细说明交易成功完成并符合Markov属性之前完成交易的步骤来验证的。

该分析假设以下假设：在给定行业中, 为了使用时间均质的马尔可夫链, 在我们的销售过程中, 给定交易在每个月中前进的概率是恒定的。那是一个马尔可夫链, 其中状态之间的转移概率随着时间的推移而保持不变(步数k增加)。

计算出的概率如下：

交易从我们的销售代表阶段转移到我们的帐户执行阶段的概率与在给定月份内保持交易的概率。
交易从我们的客户执行阶段转移到成功完成交易的可能性, 而不是在给定的月份内停留的可能性。
停留在成功完成交易的概率为1。因此, 使完成交易成为吸收状态。

该分析是使用R编程语言进行的。 R有一个方便的包, 称为Markov链, 可以处理大量Markov链类型。

首先, 我们要做的第一件事是检查我们的销售顺序是否遵循Markov属性。为此, 马尔可夫链程序包带有一个方便的函数, 称为verifyMarkovProperty(), 该函数通过对从事件序列派生的一系列列联表进行卡方检验, 来测试给定事件序列是否遵循Markov属性。大的p值表明, 不应拒绝遵循Markov属性的序列的零假设。下面提供了一个示例销售顺序, 该示例显示了从第一次会议到结束交易为止每个月的交易位置：

library(markovchain)
library(dplyr)
# SDR Funnel is our sales representative stages, AE Funnel is our account executive stages, and CW is a successfully closed deal
seq <- c('SDR Funnel', 'SDR Funnel', 'AE Funnel', 'AE Funnel', 'AE Funnel', 'AE Funnel', 'AE Funnel', 'AE Funnel', 'CW')
verifyMarkovProperty(seq)

## Testing markovianity property on given data sequence
## Chi - square statistic is: 0.5733333  degrees of freedom are: 27  and corresponding p-value is: 1

由于显示的p值大于0.05, 因此我们不会拒绝该序列遵循Markov属性的原假设。

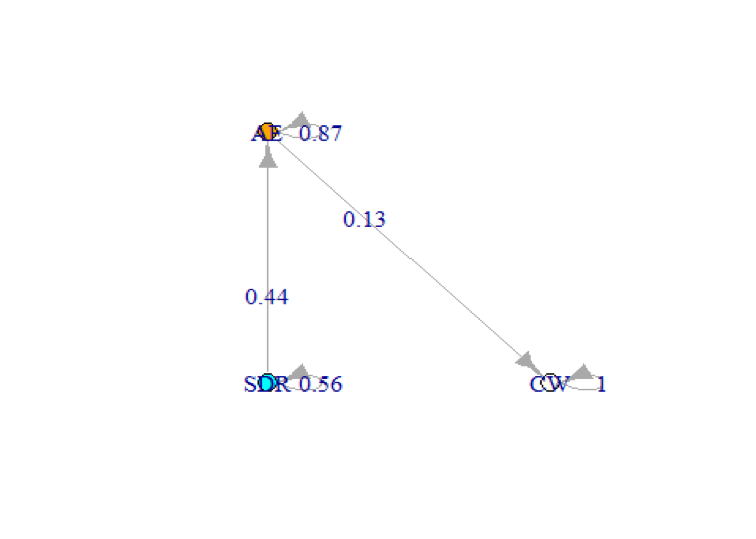
经过验证后, 我们将绘制马尔可夫链结构以及从我们的数据中得出的转移概率。该代码通过定义过渡矩阵以及状态名称来实例化Markov链对象。它还显示了马尔可夫链和转移概率。

source('TransProb.R')
source('MatDataBase.R')
source('GatherTransMat.R')
transElec <- GatherTransMat('Manufacturing', 'Between 100M and 500M', 'Between 500 and 1k')

print(transElec)

markov2 <- new('markovchain', transitionMatrix = transElec, # These are the transition probabilities of a random industry
              states = c('SDR', 'AE', 'CW'))

layout <- matrix(c(0, 0, 0, 1, 1, 0), ncol = 2, byrow = TRUE)
plot(markov2, node.size = 10, layout = layout)

##           [, 1]      [, 2]      [, 3]
## [1, ] 0.5573215 0.4426785 0.0000000
## [2, ] 0.0000000 0.8678118 0.1321882
## [3, ] 0.0000000 0.0000000 1.0000000

由于我们有一个吸收马尔可夫链, 因此我们可以计算出直至吸收的预期时间。矢量的第一个条目将输出预期的步数, 直到从SDR漏斗关闭为止；如果从AE漏斗开始, 第二个条目将输出期望的步数。

# Extract Q from the transition matrix
Q <- transElec[1:2, 1:2]
# Generate It
It <- diag(2)
#Calculate fundamental matrix
N <- solve(It-Q)
#Generate column vector of 1s
one <- t(t(c(1, 1)))

# Calculate the expected steps by matrix multiplication
expected <- N%*%one
print(expected)

##          [, 1]
## [1, ] 9.823945
## [2, ] 7.564969

但是, 我们还可以直观地看到概率随着步数的增加而变化, 从而与预期的步数进行对比。因此, 我们还检查了24个步骤中三个阶段中任何一个阶段的交易概率。

library(ggplot2)

initState <- c(1, 0, 0) # The initial state will be SDR Funnel (mimicking setting an initial discovery appointment)

# Initiate probability vectors
SDRProb <- c()
AEProb <- c()
CW <- c()

# Calculate probabilities for 24 steps.
for(k in 1:24){
  nsteps <- initState*markov2^k
  SDRProb[k] <- nsteps[1, 1]
  AEProb[k] <- nsteps[1, 2]
  CW[k] <- nsteps[1, 3]
}

# Make dataframes and merge them
SDRProb <- as.data.frame(SDRProb)
SDRProb$Group <- 'SDR'
SDRProb$Iter <- 1:24
names(SDRProb)[1] <- 'Value'

AEProb <- as.data.frame(AEProb)
AEProb$Group <- 'AE'
AEProb$Iter <- 1:24
names(AEProb)[1] <- 'Value'

CW <- as.data.frame(CW)
CW$Group <- 'CW'
CW$Iter <- 1:24
names(CW)[1] <- 'Value'

steps <- rbind(SDRProb, AEProb, CW)

# Plot the probabilities using ggplot
ggplot(steps, aes(x = Iter, y = Value, col = Group))+
  geom_line() +
  xlab('Chain Step') +
  ylab('Probability') +
  ggtitle('24 Step Chain Probability Prediction')+
  theme(plot.title = element_text(hjust = 0.5))

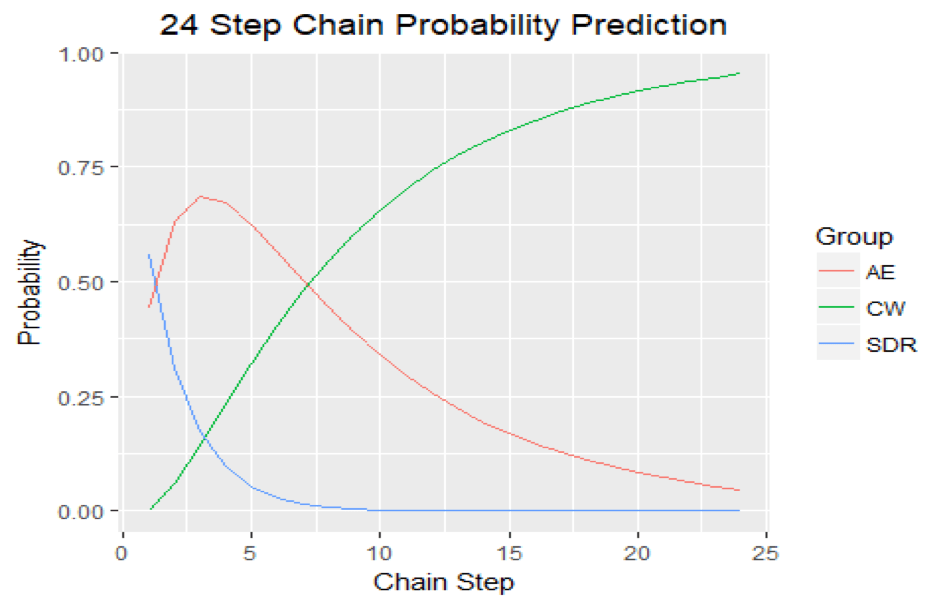
如果我们将这两个结果结合起来, 很明显CW状态在6到9步之后变成了最可能的状态。鉴于过渡可能性是每月过渡概率, 你可以辩称, 从最初任命到成功完成该行业交易的典型销售速度可能在6到9个月之间。那是一个漫长的销售过程。

总结

该分析的目的是说明如何将马尔可夫链的基本原理和吸收马尔可夫链的原理用于回答与业务相关的问题。在这种情况下, 尽管有时间同质的假设, 但马尔可夫链的结果还是相当准确的, 因为进一步的经验分析表明, 该分析中使用的行业平均销售速度为208天, 几乎是7个月。希望这个例子可以帮助你自己进一步探索马尔可夫链, 并将其应用于你的业务问题。

如果你有兴趣了解有关R的更多信息, 请参加srcmini的Intermediate R课程。

本文概述

什么是马尔可夫链？

什么是吸收马尔可夫链？

销售速度分析

总结

猜你喜欢