本文概述
如果你想了解有关电子表格的更多信息, 请参加srcmini的”电子表格统计简介”课程。
现实生活中的业务系统本质上是动态的。对于市场研究人员来说, 设计一种可以捕获所有信息的概率模型并不容易。这意味着研究人员需要更多复杂的模型来了解随着业务流程的发展而发生的客户行为。在一段时间内增长的业务流程的概率模型称为随机流程。随机过程描述了一段时间内的消费者行为。马尔可夫链是执行基于当前状态以预测客户未来状态的随机过程的技术之一。
马尔可夫分析技术以俄罗斯数学家安德烈·安德烈耶维奇·马尔科夫(Andrei Andreyevich Markov)的名字命名, 后者介绍了随机过程的研究, 随机过程是涉及机会操作的过程(来源)。该分析有助于生成新的随机但相关事件序列, 该序列看起来与原始事件相似。在分析相关的随机事件(即仅取决于最后发生的事件)时很有用。马尔可夫分析是一种概率技术, 通过提供各种结果的概率描述来帮助决策过程。
在本教程中, 你将学习马尔可夫分析, 并且将涵盖以下主题:
- 什么是马尔可夫分析?
- 术语
- 马尔可夫分析的例子
- 在电子表格中执行马尔可夫分析
- 利弊
- 总结
什么是马尔可夫分析?
马尔可夫模型是基于随机的模型, 用于对随机变化的系统进行建模。它假定将来的事件将仅取决于当前事件, 而不取决于过去的事件。它会导致未来事件发生的可能性, 以供决策。
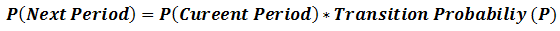
马尔可夫模型的假设:
- 从一个国家转移到所有其他国家的概率加起来等于一个。
- 概率适用于所有系统参与者。
- 概率随时间是恒定的, 并且
- 状态随着时间的推移是独立的。
你有一组状态S = {S_1, S_2, S_3…….S_r}。该过程从这些过程之一开始, 并从一种状态连续转移到另一种状态。如果系统当前位于Si处, 则它会以Pij的概率移动到下一步的状态Sj, 并且该概率不取决于系统在当前状态之前处于哪个状态。
资料来源:https://www.dartmouth.edu/~chance/teaching_aids/books_articles/probability_book/Chapter11.pdf

术语
- 随机过程:它处理由某个集合索引的随机变量的集合, 以便你可以研究系统的动力学。
- 独立事件:以抛硬币为例来理解这一点的最好方法之一, 因为每次抛硬币时, 它都不会记住上次发生的事情。头和尾的顺序不相关;因此, 它们是独立的事件。
- 相关事件:如果结果第一个事件影响另一个事件的结果, 则两个事件被认为是相关的。
- 随机变量:一个变量, 其值取决于随机实验/现象的结果。
- 稳态概率:当你继续进行马尔可夫过程时, 你会发现系统经过大量周期后处于特定状态的概率与系统的初始状态无关。在几次转换后发现的概率称为稳态概率。
来源:《管理科学定量决策方法简介》, 作者:David R. Anderson, Dennis J. Sweeney, Thomas A. Williams, Jeffrey D. Camm, R。Kipp Martin
马尔可夫分析的例子
让我们分析一下墨菲的Foodliner和阿什利的超市杂货店的市场份额和客户忠诚度。我们的主要重点是检查客户购物之旅的顺序。你可以假设客户每周可以去Murphy的Foodline或Ashley的Supermarket购物一次, 但不能两者都购物。
使用马尔可夫过程的术语, 你将每周的时间或购物旅行称为过程的试验。在每次试用中, 客户都可以在Murphy的Foodliner或Ashley的Supermarket中购物。在给定的一周内选择的特定商店称为该周内的系统状态, 因为客户在每次试用中都有两种选择或购物状态。使用有限数量的状态, 你可以按以下方式识别状态:
- 状态1:客户在墨菲的Foodliner购物。
- 状态2:客户在Ashley的超市购物。给定的转换概率为:
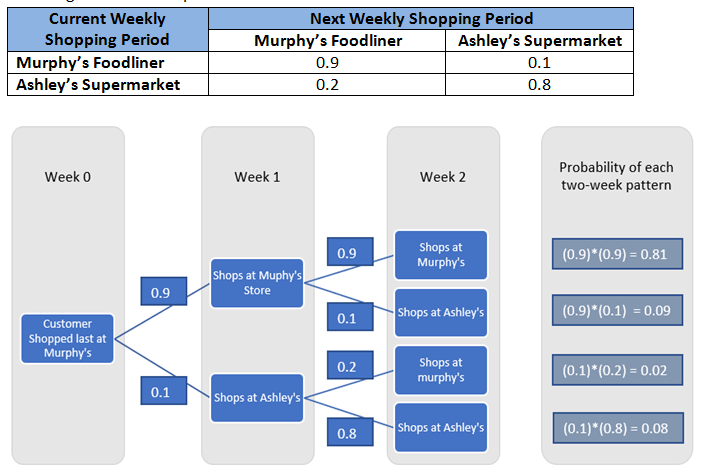
同样,
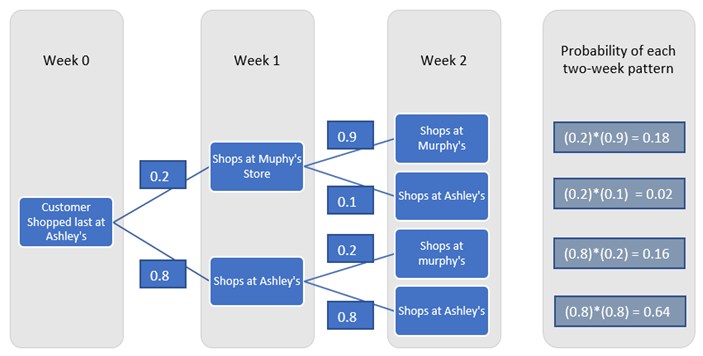
因此, 可以通过将当前状态概率矩阵与过渡概率矩阵相乘以获得下一个状态的概率, 来计算两周后的墨菲概率。
推广公式:
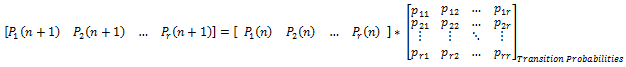
其中P1, P2, …, Pr表示处于流程状态概率的系统, 而n表示状态。
来源:《管理科学定量决策方法简介》, 作者:David R. Anderson, Dennis J. Sweeney, Thomas A. Williams, Jeffrey D. Camm, R。Kipp Martin
在电子表格中执行马尔可夫分析
让我们使用Microsoft excel解决相同的问题–
第1步:假设一开始, 有些客户是从墨菲那里购物的, 有些是从阿什利那里购物的。这可以用身份矩阵表示, 因为在墨菲(Murphy)的客户可以同时在阿什利(Ashley)的客户, 反之亦然。
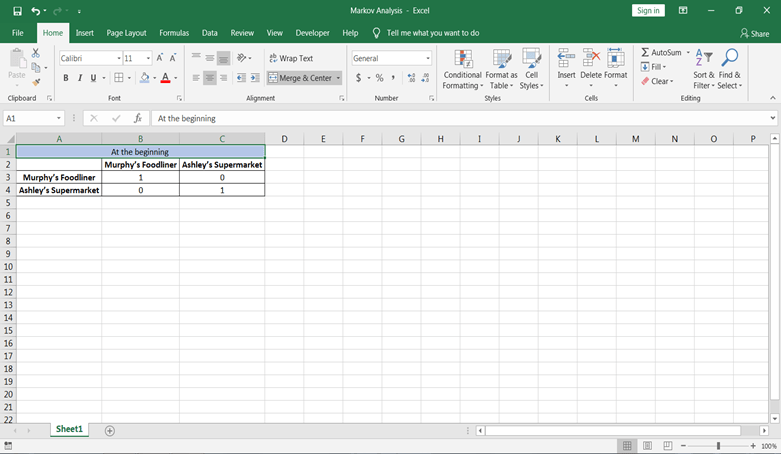
第2步:让我们还为转移概率矩阵创建一个表格。
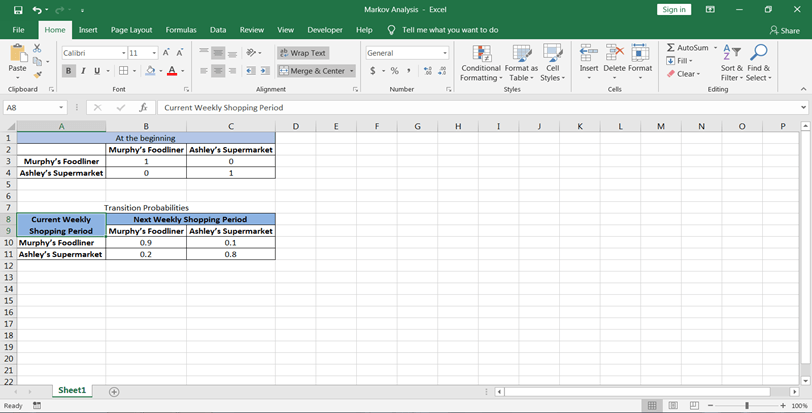
第3步:现在, 你希望在第一时间在两个商店都拥有概率:首先, 让我们设计一个表, 在其中要计算值:
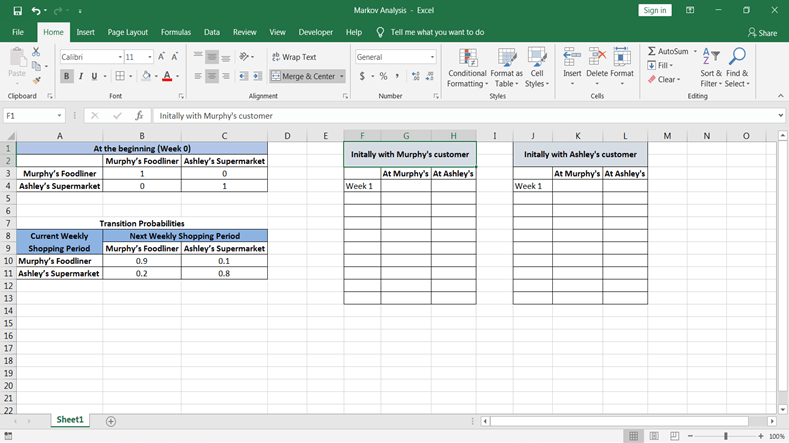
步骤4:现在, 让我们计算从墨菲的客户开始的未来时期的状态概率。可以使用excel函数= MMULT(array1, array2)计算概率。要使用此功能, 请在第1周后先在Murphy客户表中选择两个单元格。
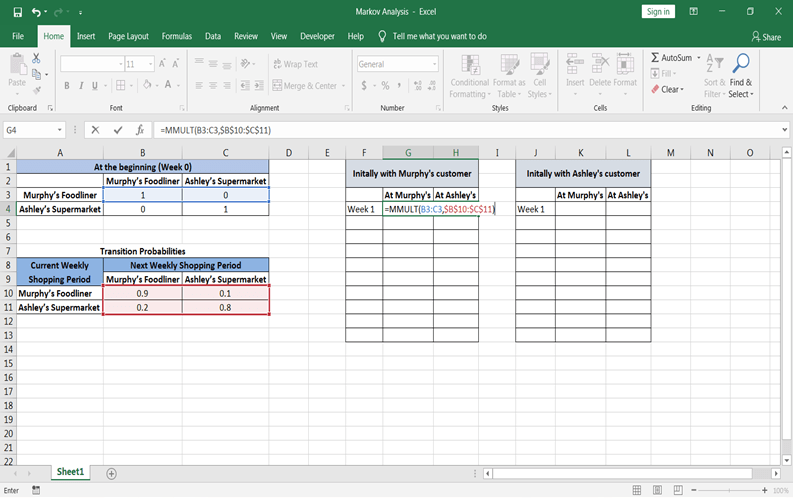
应用此公式后, 关闭公式括号, 然后同时按Control + Shift + Enter。然后, 你将看到概率值。
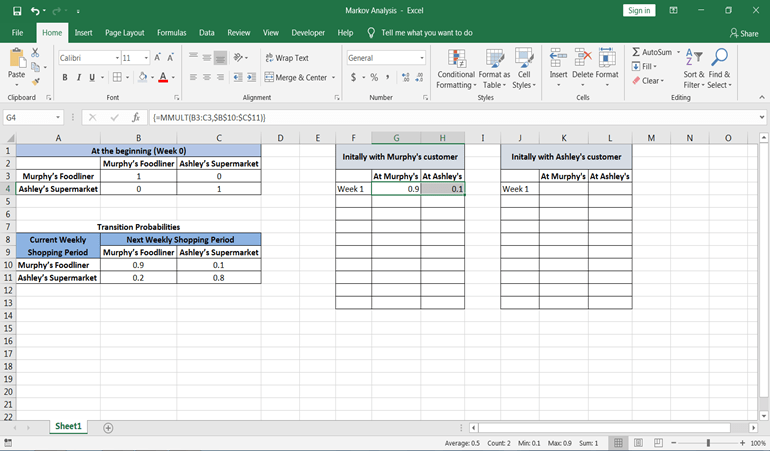
第5步:现在你已经类似地计算了状态1和第1周的概率, 因此请计算状态2。唯一会改变的是当前状态概率。将考虑一周的概率来计算未来的状态概率。
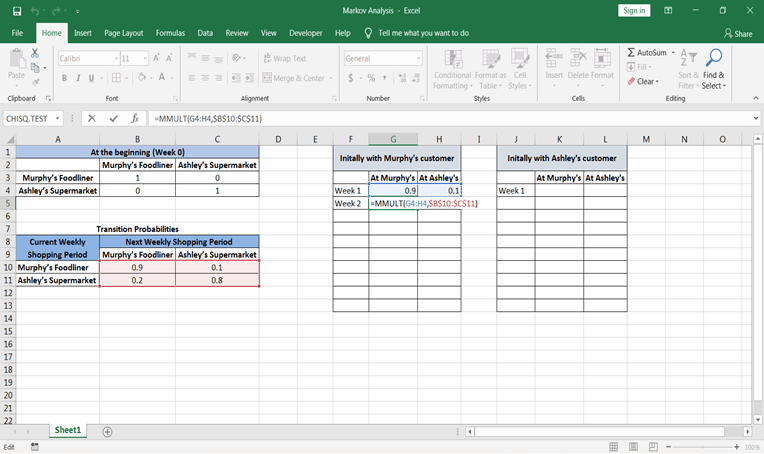
现在, 你只需从墨菲和阿什利的周单元格中复制公式, 然后粘贴到所需的单元格中即可。
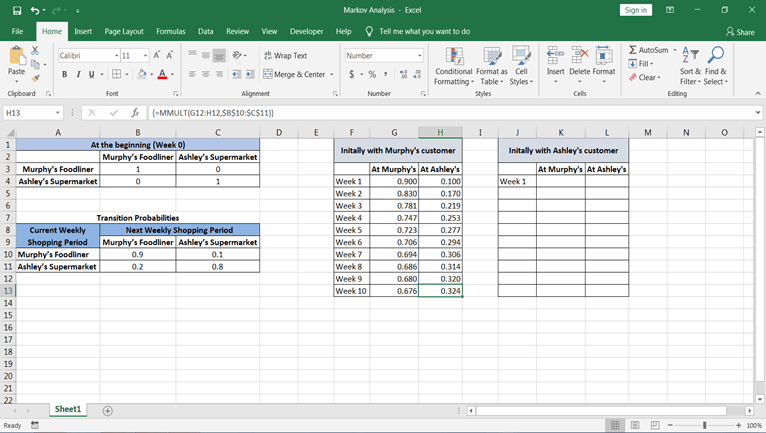
如果你最初有1000位Murphy客户(也就是说, 最后有1000位顾客在Murphy商店购物), 则我们的分析表明, 在第五个每周购物期间, 墨菲的潜在顾客为723位, 阿什利的潜在顾客为277位。此外, 在第10个每周的购物期间, 墨菲(Murphy)的潜在客户为676, 阿什利(Ashley)的潜在客户为324。
来源:《管理科学定量决策方法简介》, 作者:David R. Anderson, Dennis J. Sweeney, Thomas A. Williams, Jeffrey D. Camm, R。Kipp Martin
第6步:类似地, 现在让我们计算最初从墨菲的客户开始的未来时期的状态概率。
第一周:
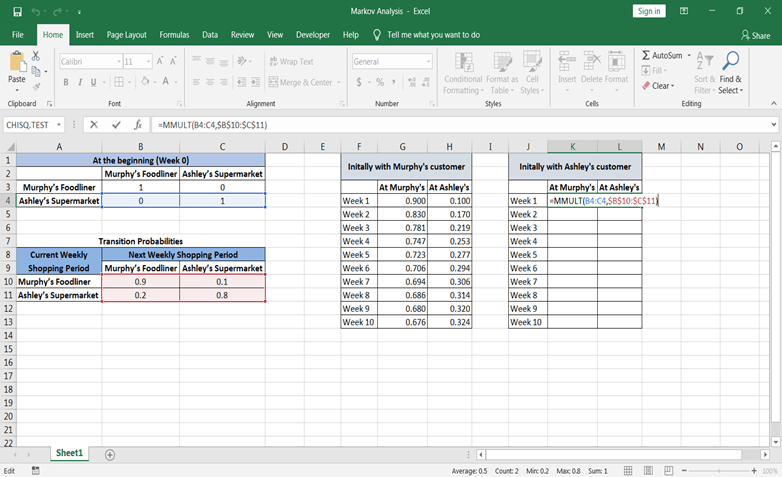
第2周:
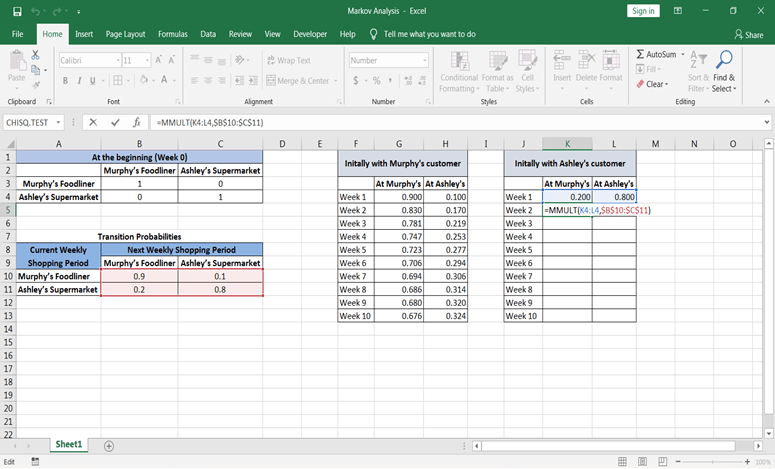
只需将公式从第2周拖到所需的时间即可。
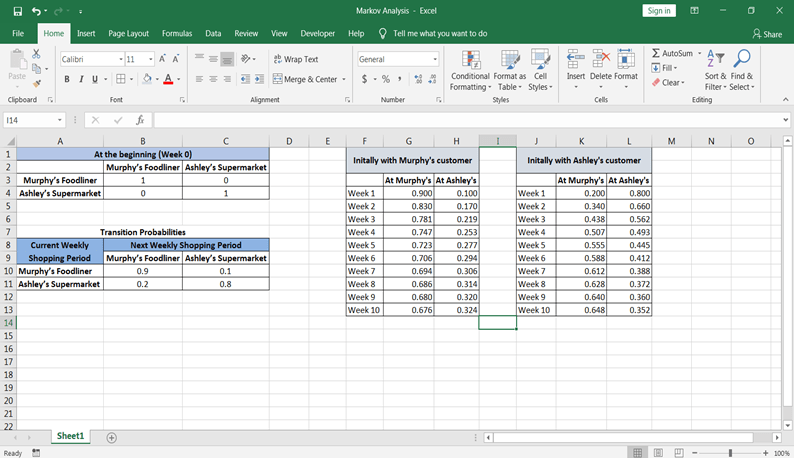
在第五个购物期间, 客户将在墨菲(Murphy)购物的概率为0.555, 而客户将在阿什利(Ashley)购物的概率为0.445。在第十阶段, 客户在墨菲(Murphy)购物的概率为0.648, 客户在阿什利(Ashley)购物的概率为0.352。
来源:《管理科学定量决策方法简介》, 作者:David R. Anderson, Dennis J. Sweeney, Thomas A. Williams, Jeffrey D. Camm, R。Kipp Martin
你还可以以图形的方式查看份额在墨菲的情况下是如何下降的, 而在最近购物于墨菲的客户的阿什利的情况下, 份额是如何增加的。
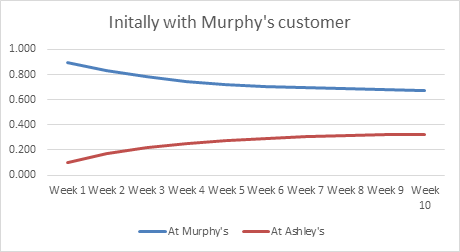
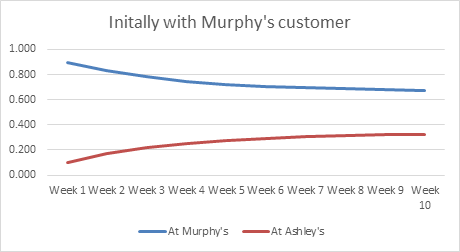
利弊
优点:
- 由于其分析性质, 它具有速度和准确性的优势。
- 与Monte-Carlo Simulation相比, 它也更快, 更准确。
- 马尔可夫模型相对容易从连续数据中得出。
- 过渡矩阵总结了动态变化的所有基本参数。
- 它使你可以深入了解系统随时间的变化。
缺点:
- 马尔可夫属性假设可能对正在建模的系统无效;这就是为什么需要仔细设计模型的原因。
- 客户可以随时进入和离开市场, 因此市场永远不会稳定。
- 在缺少早期信息的情况下, 马尔可夫分析无法预测未来的结果。
总结
恭喜, 你已完成本教程的结尾!
在本教程中, 你涵盖了许多有关马尔可夫分析的细节。你已经了解了什么是马尔可夫分析, 马尔可夫分析中使用的术语, 马尔可夫分析的示例以及如何在电子表格中求解马尔可夫分析的示例。另外, 讨论了它的优缺点。
希望你现在可以在市场营销分析中使用马尔可夫分析概念。感谢你阅读本教程!



