正则化：Ridge，Lasso和Elastic Net

本文概述

多元回归中的偏差-偏差权衡
岭回归
套索回归
岭回归 VS 套索回归
Elastic Net弹性网络
总结

我们将介绍方法的数学属性以及实际的R示例, 以及一些其他的调整和技巧。事不宜迟, 让我们开始吧！

多元回归中的偏差-偏差权衡

让我们从基础开始：简单的线性回归模型, 其中的目标是通过m个预测变量X和具有方差σ2的正态分布误差项的线性组合来预测n个观测到的响应变量Y。

由于我们不知道真正的参数β, 因此我们必须从样本中估算出它们。在普通最小二乘(OLS)方法中, 我们以这样的方式将它们估计为$ \ hat \ beta $, 即残差的平方和尽可能小。换句话说, 我们最小化了以下损失函数：

为了获得臭名昭著的OLS参数估计, $ \ hat \ beta_ {OLS} =(X’X)^ {-1}(X’Y)$。

在统计中, 需要考虑两个重要的估计量特征：偏差和方差。偏差是真实总体参数与预期估计量之间的差：

它衡量估计的准确性。另一方面, 方差衡量这些估计中的价差或不确定性。它由

未知误差方差σ2可以从残差估算为

此图说明了偏差和方差是什么。想象一下, 牛眼是我们正在估计的真实总体参数β, 而它的镜头是我们的估计值, 它是由四个不同的估计量得出的-低偏差和方差, 高偏差和方差及其组合。

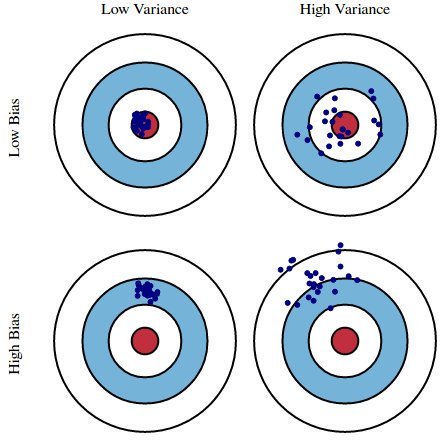
期望偏差和方差都较低, 因为较大的值会导致模型预测不佳。实际上, 模型的误差可以分解为三个部分：由大方差引起的误差, 由显着偏差引起的误差以及其余部分(无法解释的部分)。

OLS估计器具有无偏的期望属性。但是, 它可能会有很大的差异。具体而言, 在以下情况下会发生这种情况：

预测变量彼此高度相关；
有许多预测因素。这反映在上面给出的方差公式中：如果m接近n, 则方差接近无穷大。

通用的解决方案是：以引入一些偏差为代价来减少方差。这种方法称为正则化, 几乎总是对模型的预测性能有利。为了使它沉入, 让我们看一下下面的图。

随着模型复杂度的增加(在线性回归的情况下, 可以将其视为预测变量的数量), 估计的方差也会增加, 但偏差会减少。无偏的OLS会将我们置于图片的右侧, 这远非最佳。这就是我们进行正则化的原因：以某种偏见为代价降低方差, 从而使曲线图的左侧向最优方向移动。

岭回归

通过到目前为止的讨论, 我们得出的结论是, 我们希望降低模型的复杂性, 即预测变量的数量。为此, 我们可以使用前向或后向选择, 但是那样一来, 我们将无法告知任何有关已删除变量对响应的影响的信息。从模型中删除预测变量可以看作是将其系数设置为零。与其强迫它们完全不为零, 不如让它们离零太远, 而对其进行惩罚, 从而以连续的方式使它们变小。这样, 我们在保留所有变量的同时降低了模型的复杂性。基本上, 这就是Ridge回归所做的。

型号规格

在Ridge回归中, OLS损失函数的增加方式使得我们不仅最小化残差平方和, 而且对参数估计的大小进行惩罚, 以将其缩小为零：

为$ \ hat \ beta $求解此函数可得到岭回归估计$ \ hat \ beta_ {ridge} =(X’X + \ lambda I)^ {-1}(X’Y)$, 其中, 我表示单位矩阵。

λ参数是正则化惩罚。在本教程的下一部分中, 我们将讨论如何选择它, 但现在请注意：

作为$ \ lambda \ rightarrow 0, \ quad \ hat \ beta_ {ridge} \ rightarrow \ hat \ beta_ {OLS} $;
作为$ \ lambda \ rightarrow \ infty, \ quad \ hat \ beta_ {ridge} \ rightarrow 0 $。

因此, 将λ设置为0与使用OLS相同, 但其值越大, 系数的大小越受惩罚。

岭回归中的偏差-偏差权衡

将正则化系数纳入偏差和方差的公式中可得出

从那里你可以看到, 随着λ变大, 方差减小, 并且偏差增大。这就提出了一个问题：为了减少差异, 我们愿意接受多少偏差？或者：λ的最佳值是多少？

正则化参数的选择

我们可以通过两种方式解决此问题。一种更传统的方法是选择λ, 以使某些信息标准(例如AIC或BIC)最小。类似于机器学习的方法是执行交叉验证并选择λ的值, 该值使交叉验证的平方残差之和(或其他度量)最小化。前一种方法强调模型对数据的拟合, 而后一种方法则更侧重于其预测性能。让我们一起讨论。

最小化信息标准

这种方法可以归结为使用λ的许多不同值来估计模型, 然后选择一个最小化Akaike或Bayesian信息准则的模型：

其中dfridge是自由度的数量。注意这里！岭回归中的自由度数与常规OLS中的自由度数不同！通常会忽略这一点, 从而导致错误的推断。在OLS和岭回归中, 自由度都等于所谓的hat矩阵的踪迹, 该矩阵是将响应值的向量映射到拟合值的向量的矩阵, 如下所示：$ \ hat y = H y $。

在OLS中, 我们发现HOLS = X(X’X)−1X, 得到dfOLS = trHOLS = m, 其中m是预测变量的数量。但是, 在岭回归中, 帽子矩阵的公式应包括正则化惩罚：Hridge = X(X’X +λI)-1X, 得出dfridge = trHridge, 该值不再等于m。某些ridge回归软件会基于OLS公式生成信息标准。为确保你做的正确, 手动计算它们会更安全, 这是我们在本教程的稍后部分中要做的。

最小化交叉验证的残差

要通过交叉验证选择λ, 你应该选择一组λ的P值进行测试, 将数据集拆分为K折, 然后遵循以下算法：

对于1：P中的p：
对于1：K中的k：
保留倍数k作为保留数据
使用剩余的倍数和λ=λp来估计$ \ hat \ beta_ {ridge} $
预测保留数据：$ y_ {test, k} = X_ {test, k} \ hat \ beta_ {ridge} $
计算残差平方和：SSRk = || y − ytest, k || 2
以k结尾
平均SSR：$ SSR_ {p} = \ frac {1} {K} \ sum_ {k = 1} ^ {K} SSR_ {k} $
以p结尾
选择最佳值：λopt= argminpSSRp

当然, 你无需自己编程-R具有所有专用功能。

岭回归：R示例

在R中, glmnet软件包包含实现ridge回归所需的全部。我们将以臭名昭著的mtcars数据集为例, 其中的任务是根据汽车的其他特征预测每加仑的英里数。还有一件事：山脊回归假设预测变量是标准化的, 并且响应居中！你很快就会明白为什么需要这种假设。现在, 我们只是在建模之前进行标准化。

# Load libraries, get data & set seed for reproducibility ---------------------
set.seed(123)    # seef for reproducibility
library(glmnet)  # for ridge regression
library(dplyr)   # for data cleaning
library(psych)   # for function tr() to compute trace of a matrix

data("mtcars")
# Center y, X will be standardized in the modelling function
y <- mtcars %>% select(mpg) %>% scale(center = TRUE, scale = FALSE) %>% as.matrix()
X <- mtcars %>% select(-mpg) %>% as.matrix()


# Perform 10-fold cross-validation to select lambda ---------------------------
lambdas_to_try <- 10^seq(-3, 5, length.out = 100)
# Setting alpha = 0 implements ridge regression
ridge_cv <- cv.glmnet(X, y, alpha = 0, lambda = lambdas_to_try, standardize = TRUE, nfolds = 10)
# Plot cross-validation results
plot(ridge_cv)

# Best cross-validated lambda
lambda_cv <- ridge_cv$lambda.min
# Fit final model, get its sum of squared residuals and multiple R-squared
model_cv <- glmnet(X, y, alpha = 0, lambda = lambda_cv, standardize = TRUE)
y_hat_cv <- predict(model_cv, X)
ssr_cv <- t(y - y_hat_cv) %*% (y - y_hat_cv)
rsq_ridge_cv <- cor(y, y_hat_cv)^2


# Use information criteria to select lambda -----------------------------------
X_scaled <- scale(X)
aic <- c()
bic <- c()
for (lambda in seq(lambdas_to_try)) {
  # Run model
  model <- glmnet(X, y, alpha = 0, lambda = lambdas_to_try[lambda], standardize = TRUE)
  # Extract coefficients and residuals (remove first row for the intercept)
  betas <- as.vector((as.matrix(coef(model))[-1, ]))
  resid <- y - (X_scaled %*% betas)
  # Compute hat-matrix and degrees of freedom
  ld <- lambdas_to_try[lambda] * diag(ncol(X_scaled))
  H <- X_scaled %*% solve(t(X_scaled) %*% X_scaled + ld) %*% t(X_scaled)
  df <- tr(H)
  # Compute information criteria
  aic[lambda] <- nrow(X_scaled) * log(t(resid) %*% resid) + 2 * df
  bic[lambda] <- nrow(X_scaled) * log(t(resid) %*% resid) + 2 * df * log(nrow(X_scaled))
}

# Plot information criteria against tried values of lambdas
plot(log(lambdas_to_try), aic, col = "orange", type = "l", ylim = c(190, 260), ylab = "Information Criterion")
lines(log(lambdas_to_try), bic, col = "skyblue3")
legend("bottomright", lwd = 1, col = c("orange", "skyblue3"), legend = c("AIC", "BIC"))

# Optimal lambdas according to both criteria
lambda_aic <- lambdas_to_try[which.min(aic)]
lambda_bic <- lambdas_to_try[which.min(bic)]

# Fit final models, get their sum of squared residuals and multiple R-squared
model_aic <- glmnet(X, y, alpha = 0, lambda = lambda_aic, standardize = TRUE)
y_hat_aic <- predict(model_aic, X)
ssr_aic <- t(y - y_hat_aic) %*% (y - y_hat_aic)
rsq_ridge_aic <- cor(y, y_hat_aic)^2

model_bic <- glmnet(X, y, alpha = 0, lambda = lambda_bic, standardize = TRUE)
y_hat_bic <- predict(model_bic, X)
ssr_bic <- t(y - y_hat_bic) %*% (y - y_hat_bic)
rsq_ridge_bic <- cor(y, y_hat_bic)^2


# See how increasing lambda shrinks the coefficients --------------------------
# Each line shows coefficients for one variables, for different lambdas.
# The higher the lambda, the more the coefficients are shrinked towards zero.
res <- glmnet(X, y, alpha = 0, lambda = lambdas_to_try, standardize = FALSE)
plot(res, xvar = "lambda")
legend("bottomright", lwd = 1, col = 1:6, legend = colnames(X), cex = .7)

异方差岭回归

我之前已经提到过, 岭回归假设预测变量按比例缩放到z分数。为什么要这样做？这种缩放比例确保了惩罚项对每个系数均等地惩罚, 使得其形式为$ \ lambda \ sum_ {j = 1} ^ m \ hat \ beta_j ^ 2 $。如果预测变量不是标准化的, 则它们的标准偏差不都等于1, 并且可以通过一些数学运算来证明这将导致惩罚项形式为$ \ lambda \ sum_ {j = 1} ^ m \ hat \ beta_j ^ 2 / std(x_j)$。因此, 然后将未标准化的系数通过其相应预测变量的标准偏差的倒数加权。我们通过缩放X矩阵来避免这种情况, 但是…除了通过缩放来均衡所有预测变量的方差来解决该异方差问题之外, 我们还可以在估计过程中将它们用作权重！这就是差分加权或异方差岭回归的思想。

这个想法是通过对损失函数引入权重来惩罚具有不同强度的不同系数：

如何选择权重wj？对所有预测变量运行一组单变量回归(响应与一个预测变量), 提取系数方差的估计值$ \ hat \ sigma_ {j} $, 并将其用作权重！这条路：

$ \ hat \ sigma_ {j} $较小的变量$ \ hat \ beta_j $, 因此估算中的不确定性较小, 因此惩罚较少；
$ \ hat \ sigma_ {j} $较大的变量$ \ hat \ beta_j $会受到严重的惩罚, 因此估算中的不确定性很大。

这是在R中执行此操作的方法。由于该方法未在glmnet中实现, 因此我们需要在此处进行一些编程。

# Calculate the weights from univariate regressions
weights <- sapply(seq(ncol(X)), function(predictor) {
  uni_model <- lm(y ~ X[, predictor])
  coeff_variance <- summary(uni_model)$coefficients[2, 2]^2
})


# Heteroskedastic Ridge Regression loss function - to be minimized
hridge_loss <- function(betas) {
  sum((y - X %*% betas)^2) + lambda * sum(weights * betas^2)
}


# Heteroskedastic Ridge Regression function
hridge <- function(y, X, lambda, weights) {
  # Use regular ridge regression coefficient as initial values for optimization
  model_init <- glmnet(X, y, alpha = 0, lambda = lambda, standardize = FALSE)
  betas_init <- as.vector(model_init$beta)
  # Solve optimization problem to get coefficients
  coef <- optim(betas_init, hridge_loss)$par
  # Compute fitted values and multiple R-squared
  fitted <- X %*% coef
  rsq <- cor(y, fitted)^2
  names(coef) <- colnames(X)
  output <- list("coef" = coef, "fitted" = fitted, "rsq" = rsq)
  return(output)
}


# Fit model to the data for lambda = 0.001
hridge_model <- hridge(y, X, lambda = 0.001, weights = weights)
rsq_hridge_0001 <- hridge_model$rsq

# Cross-validation or AIC/BIC can be employed to select some better lambda!
# You can find some useful functions for this at https://github.com/MichalOleszak/momisc/blob/master/R/hridge.R

套索回归

套索或最小绝对收缩和选择算子在概念上与山脊回归非常相似。它还对非零系数增加了惩罚, 但是与脊回归不惩罚平方系数的和(所谓的L2惩罚)不同, 套索惩罚了绝对系数的和(L1惩罚)。结果, 对于较高的λ值, 在套索下许多系数都被完全归零, 而在脊回归中却从来没有这样。

型号规格

岭损失函数和套索损失函数的唯一区别在于惩罚项。在套索下, 损失定义为：

套索：R示例

要运行套索回归, 你可以重新使用glmnet()函数, 但是将alpha参数设置为1。

# Perform 10-fold cross-validation to select lambda ---------------------------
lambdas_to_try <- 10^seq(-3, 5, length.out = 100)
# Setting alpha = 1 implements lasso regression
lasso_cv <- cv.glmnet(X, y, alpha = 1, lambda = lambdas_to_try, standardize = TRUE, nfolds = 10)
# Plot cross-validation results
plot(lasso_cv)

# Best cross-validated lambda
lambda_cv <- lasso_cv$lambda.min
# Fit final model, get its sum of squared residuals and multiple R-squared
model_cv <- glmnet(X, y, alpha = 1, lambda = lambda_cv, standardize = TRUE)
y_hat_cv <- predict(model_cv, X)
ssr_cv <- t(y - y_hat_cv) %*% (y - y_hat_cv)
rsq_lasso_cv <- cor(y, y_hat_cv)^2


# See how increasing lambda shrinks the coefficients --------------------------
# Each line shows coefficients for one variables, for different lambdas.
# The higher the lambda, the more the coefficients are shrinked towards zero.
res <- glmnet(X, y, alpha = 1, lambda = lambdas_to_try, standardize = FALSE)
plot(res, xvar = "lambda")
legend("bottomright", lwd = 1, col = 1:6, legend = colnames(X), cex = .7)

岭回归 VS 套索回归

让我们比较我们估计的各种模型的多个R平方！

rsq <- cbind("R-squared" = c(rsq_ridge_cv, rsq_ridge_aic, rsq_ridge_bic, rsq_hridge_0001, rsq_lasso_cv))
rownames(rsq) <- c("ridge cross-validated", "ridge AIC", "ridge BIC", "hridge 0.001", "lasso cross_validated")
print(rsq)

##                       R-squared
## ridge cross-validated 0.8536968
## ridge AIC             0.8496310
## ridge BIC             0.8412011
## hridge 0.001          0.7278277
## lasso cross_validated 0.8426777

它们对于这些数据的表现似乎相似。请记住, 异方差模型是未调整的, 而lambda并不是最优的！关于ridge和套索比较的一些更一般的考虑：

通常, 两个人的整体状况都不佳。
套索可以将某些系数设置为零, 从而执行变量选择, 而岭回归则不能。
两种方法都允许使用相关的预测变量, 但是它们以不同的方式解决多重共线性问题：
- 在岭回归中, 相关预测因子的系数相似。
- 在套索中, 一个相关的预测变量的系数较大, 而其余的(几乎)为零。
如果有少量有效参数, 而其他参数接近零(通常只有几个预测变量实际影响响应), 则套索往往表现良好。
如果有许多大约相同值的大参数, Ridge效果很好(ergo：大多数预测变量会影响响应)。
但是, 在实践中, 我们不知道真正的参数值, 因此前两点在理论上是有些许的。只需运行交叉验证, 即可为特定情况选择更合适的模型。
或者…结合两者！

Elastic Net弹性网络

Elastic Net最初是由于对套索的批评而出现的, 套索的变量选择可能过于依赖数据, 因此不稳定。解决方案是将岭回归和套索的惩罚结合起来, 以获得两全其美的效果。 Elastic Net旨在最小化以下损失函数：

其中α是脊(α= 0)和套索(α= 1)之间的混合参数。

现在, 有两个参数需要调整：λ和α。 glmnet程序包允许通过交叉验证对固定的α进行λ调谐, 但是它不支持α调谐, 因此我们将转向插入式。

library(caret)

# Set training control
train_control <- trainControl(method = "repeatedcv", number = 5, repeats = 5, search = "random", verboseIter = TRUE)

# Train the model
elastic_net_model <- train(mpg ~ ., data = cbind(y, X), method = "glmnet", preProcess = c("center", "scale"), tuneLength = 25, trControl = train_control)

# Check multiple R-squared
y_hat_enet <- predict(elastic_net_model, X)
rsq_enet <- cor(y, y_hat_enet)^2

总结

恭喜你！如果到此为止, 你已经知道：

如果你的线性模型包含许多预测变量, 或者如果这些变量相关, 则标准OLS参数估计值将具有较大的方差, 从而使模型不可靠。
为了解决这个问题, 你可以使用正则化-一种允许以引入一些偏差为代价来减少这种差异的技术。找到一个良好的偏差-方差折衷可以使模型的总误差最小。
共有三种流行的正则化技术, 每种技术都旨在减小系数的大小：
- 岭回归, 对平方系数和进行惩罚(L2罚分)。
- 套索回归, 惩罚系数的绝对值之和(L1罚分)。
- Elastic Net弹性网络, Ridge和Lasso的凸组合。
可以通过交叉验证来调整各个惩罚项的大小, 以找到模型的最佳拟合。
实现正则化线性模型的R包是glmnet。对于调整Elastic Net, 也可以使用插入号。

如果你想了解有关R中回归的更多信息, 请参加srcmini的R中的监督学习：回归课程。

本文概述

多元回归中的偏差-偏差权衡

岭回归

型号规格

岭回归中的偏差-偏差权衡

正则化参数的选择

岭回归：R示例

异方差岭回归

套索回归

型号规格

套索：R示例

岭回归 VS 套索回归

Elastic Net弹性网络

总结

猜你喜欢