人工智能中的贝叶斯定理

本文概述

贝叶斯定理也称为贝叶斯定律，贝叶斯定律或贝叶斯推理，它确定具有不确定知识的事件的概率。

在概率论中，它涉及两个随机事件的条件概率和边际概率。

贝叶斯定理以英国数学家托马斯·贝叶斯命名。贝叶斯推理是贝叶斯定理的应用，它是贝叶斯统计的基础。

这是一种基于P（A | B）的知识来计算P（B | A）值的方法。

贝叶斯定理允许通过观察现实世界的新信息来更新事件的概率预测。

示例：如果癌症与一个人的年龄相对应，则可以使用贝叶斯定理，借助年龄，我们可以更准确地确定癌症的可能性。

可以使用乘积规则和事件A与已知事件B的条件概率来得出贝叶斯定理：

根据产品规则，我们可以这样写：

P(A ⋀ B)= P(A|B) P(B) or

同样，事件B与已知事件A的概率：

P(A ⋀ B)= P(B|A) P(A)

在两个等式的右边，我们将得到：

上式（a）称为贝叶斯定律或贝叶斯定理。这个等式是大多数现代AI系统中用于概率推断的基础。

它显示了联合概率和条件概率之间的简单关系。这里，

P（A | B）被称为后验，我们需要计算它，当我们出现证据B时，它将被理解为假设A的概率。

P（B | A）称为似然性，其中我们认为假设是正确的，然后我们计算出证据的概率。

P（A）称为先验概率，即在考虑证据之前的假设概率

P（B）称为边际概率，即证据的纯概率。

通常，在等式（a）中，我们可以写成P（B）= P（A）* P（B | Ai），因此贝叶斯规则可以写成：

其中A1，A2，A3，………….. An是一组相互排斥且详尽的事件。

贝叶斯规则允许我们根据P（A | B），P（B）和P（A）计算单个项P（B | A）。在我们很有可能要确定这三个术语的情况下，这非常有用。假设我们要感知某个未知原因的影响，并要计算该原因，那么贝叶斯规则变为：

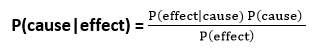
示例1：

问题：患者患有颈部僵硬的脑膜炎的可能性是多少？

给定数据：

医生知道脑膜炎会导致病人颈部僵硬，而且80%的情况下都会发生。他还了解到一些情况，情况如下:

设a为患者颈部僵硬的主张，b为患者脑膜炎的主张。，因此我们可以计算如下：

P（a | b）= 0.8

P（b）= 1/30000

P（a）= .02

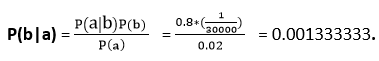
因此，我们可以假设750名患者中有1名患有脑膜炎，颈部僵硬。

示例2：

问题：从标准扑克牌中抽出一张纸牌。该牌为王的概率为4/52，然后计算后验概率P（King | Face），这表示抽奖面卡为王牌。

解：

P（国王）：卡为王的概率= 4/52 = 1/13

P（面）：一张牌是一张面牌的概率= 3/13

P（Face | King）：当我们假设它是国王时的面卡概率= 1

将所有值放在方程式（i）中，我们将得到：

以下是贝叶斯定理的一些应用：