本文概述
不确定
到目前为止,我们已经确定地使用了一阶逻辑和命题逻辑学习了知识表示,这意味着我们对谓词有把握。用这种知识表示,我们可以写成A→B,这意味着如果A为真,那么B为真,但是考虑一种情况,即我们不确定A是否为真,那么我们就无法表达该陈述,这种情况称为不确定。
因此,为了表示不确定的知识,如果我们不确定谓词,则需要不确定的推理或概率推理。
不确定原因
以下是在现实世界中发生不确定性的一些主要原因。
- 信息来自不可靠的来源。
- 实验错误
- 设备故障
- 温度变化
- 气候变化。
概率推理
概率推理是一种知识表示的方法,其中我们应用概率的概念来表示知识的不确定性。在概率推理中,我们将概率论与逻辑相结合来处理不确定性。
我们在概率推理中使用概率,因为概率提供了一种方法来处理由于某人的懒惰和无知所导致的不确定性。
在现实世界中,有很多情况无法确定某些事情的确定性,例如“今天会下雨”,“某人在某些情况下的行为”,“两支球队或两名球员之间的比赛”。这些是可能的句子,我们可以假设它们会发生但不确定,因此在这里我们使用概率推理。
人工智能中概率推理的需求:
- 当有不可预测的结果时。
- 当谓词的规范或可能性变得太大而无法处理时。
- 实验期间发生未知错误时。
在概率推理中,有两种方法可以解决不确定知识的问题:
- 贝叶斯法则
- 贝叶斯统计
注意:我们将在后面的章节中学习以上两个规则。
由于概率推理使用概率和相关术语,因此在理解概率推理之前,让我们了解一些常见术语:
概率:概率可以定义为不确定事件发生的机会。它是事件发生可能性的数字度量。概率值始终保持在0到1之间,代表理想的不确定性。
0 ≤ P(A) ≤ 1, where P(A) is the probability of an event A.P(A) = 0, indicates total uncertainty in an event A.P(A) =1, indicates total certainty in an event A.通过使用以下公式,我们可以找到不确定事件的概率。
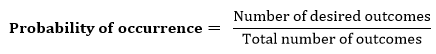
- P(¬A)=未发生事件的概率。
- P(¬A)P(A)= 1。
事件:变量的每个可能结果称为事件。
样本空间:所有可能事件的集合称为样本空间。
随机变量:随机变量用于表示现实世界中的事件和对象。
先验概率:事件的先验概率是在观察新信息之前计算出的概率。
后验概率:在考虑所有证据或信息后计算出的概率。它是先验概率和新信息的组合。
条件概率
条件概率是当另一个事件已经发生时发生一个事件的概率。
假设,我们要在事件B已经发生时计算事件A,“在B条件下A的概率”,可以写为:
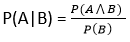
其中P(A⋀B)= a和B的联合概率
P(B)= B的边际概率
如果给定了A的概率,而我们需要找到B的概率,则它将为:
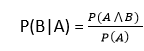
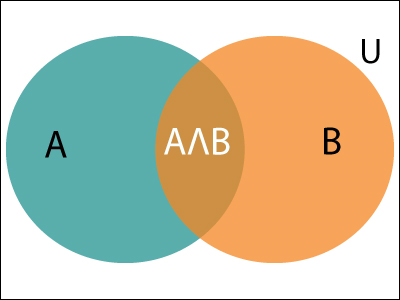
可以通过下面的维恩图来解释,其中B是事件发生的地方,因此样本空间将减少为集合B,现在我们只能通过除以P(A⋀ B)通过P(B)。
例:
在一个班级里,有70%的学生喜欢英语,40%的学生喜欢英语和数学,那么喜欢英语的学生也喜欢数学的学生比例是多少
解:
A是学生喜欢数学的活动
B是学生喜欢英语的活动。
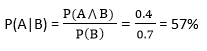
因此,57%的喜欢英语的学生也喜欢数学。



