本文概述
推理
在人工智能中,我们需要能够根据旧逻辑或证据创建新逻辑的智能计算机,因此从证据和事实中得出结论称为推理。
推理规则
推理规则是用于生成有效参数的模板。推理规则应用于人工智能中的证明,证明是得出预期目标的结论序列。
在推理规则中,所有连接词之间的含义都起着重要的作用。以下是与推理规则有关的一些术语:
- 含义:它是可以表示为P→Q的逻辑连接词之一。它是一个布尔表达式。
- 反之:蕴涵的反之,这意味着右侧的命题转到左侧,反之亦然。可以写成Q→P。
- 对立的:逆的求反被称为对立的,可以表示为Q Q→¬P。
- 逆:蕴涵的否定称为逆。它可以表示为¬P→¬Q。
从上一项可以看出,一些复合语句彼此等效,我们可以使用真值表证明这一点:
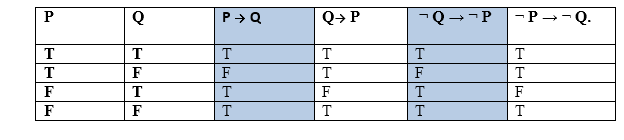
因此,从上面的真值表中,我们可以证明P→Q等于¬Q→¬P,而Q→P等于¬P→¬Q。
推理规则的类型
1.方法的posits:
Modus Ponens规则是最重要的推理规则之一,它指出如果P和P→Q为真,那么我们可以推断Q为真。它可以表示为:

例:
陈述1:“如果我困了,我就去睡觉” ==> P→Q陈述2:“我困了,我就睡” ==> P结论:“我要睡觉”。 ==>Q。因此,我们可以说,如果P→Q为真且P为真,则Q为真。
事实证明表:
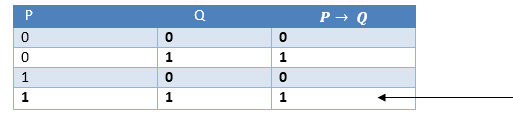
2.方法服用;
收费方式规则规定,如果P→Q为真且¬Q为真,则¬P也为真。它可以表示为:
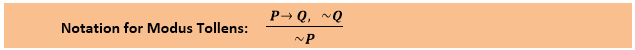
陈述1:“如果我困了,我就去睡觉” ==> P→Q陈述2:“我不去睡觉。” ==>〜Q陈述3:推断“我是不困“ =>〜P
事实证明表:

3.假设三段论:
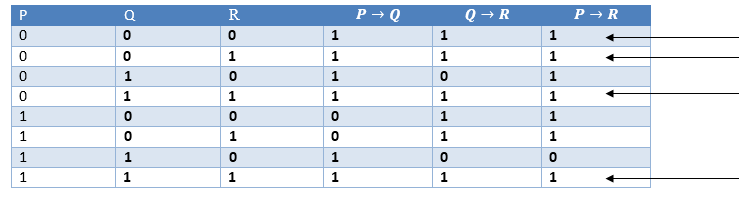
假设三段论规则指出,只要P→R为真,且P→Q为真,则P→R为真。它可以表示为以下符号:
例:
陈述1:如果你有我的主页键,则可以解锁我的主页。 P→Q陈述2:如果你可以解锁我的房屋,则可以拿走我的钱。 Q→R结论:如果你有我的主页钥匙,那么你可以拿走我的钱。 P→R
事实证明表:
4.歧义三段论:
析取三段论规则规定,如果P∨Q为真,¬P为真,则Q为真。它可以表示为:
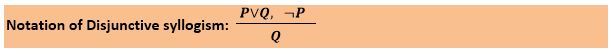
例:
陈述1:今天是星期日或星期一。 ==>P∨Q陈述2:今天不是星期日。 ==>¬P结论:今天是星期一。 ==> Q
真值表证明:

5.加法:
加法则规则是一种常见的推理规则,它指出如果P为真,则P∨Q为真。

例:
声明:我有香草冰淇淋。 ==> P陈述2:我有巧克力冰淇淋。结论:我有香草或巧克力冰淇淋。 ==>(P∨Q)
真值表证明:

6.简化:
简化规则规定,如果P∧Q为真,则Q或P也为真。它可以表示为:
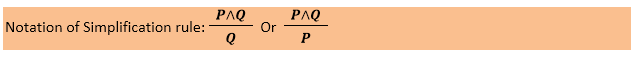
真值表证明:

7.解决方法:
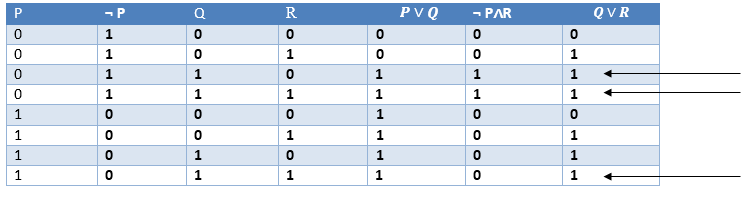
解决规则规定,如果P∨Q和¬P∧R为真,则Q∨R也为真。它可以表示为

真值表证明: