本文概述
- Alpha-beta修剪是minimax算法的修改版本。它是minimax算法的一种优化技术。
- 正如我们在minimax搜索算法中看到的那样,必须检查的游戏状态数在树的深度上呈指数级。由于我们无法消除指数,因此我们可以将其减半。因此,存在一种无需检查游戏树的每个节点就可以计算正确的minimax决策的技术,该技术称为修剪。这涉及两个阈值参数Alpha和Beta用于将来扩展,因此称为alpha-beta修剪。它也称为Alpha-Beta算法。
- Alpha-beta修剪可以应用于树的任何深度,有时它不仅可以修剪树叶,还可以修剪整个子树。
- 可以将两个参数定义为:Alpha:到目前为止,在Maximizer路径上的任何点处,我们都找到了最佳(最高值)选择。 alpha的初始值为-∞。 Beta:到目前为止,我们已经在Minimizer的任何位置找到了最佳(最低价值)选择。 beta的初始值为∞。
- 将Alpha-beta修剪为标准minimax算法会返回与标准算法相同的动作,但是会删除所有不会真正影响最终决策但会使算法变慢的节点。因此,通过修剪这些节点,可以使算法更快。
注意:为了更好地理解该主题,请研究minimax算法。
Alpha-beta修剪的条件
alpha-beta修剪所需的主要条件是:
α>=β有关alpha-beta修剪的要点
- Max播放器只会更新alpha的值。
- 最小播放器只会更新beta的值。
- 在回溯树时,节点值将传递到较高的节点,而不是alpha和beta值。
- 我们只会将alpha,beta值传递给子节点。
伪代码用于Alpha-Beta修剪
function minimax(node, depth, alpha, beta, maximizingPlayer) is
if depth ==0 or node is a terminal node then
return static evaluation of node
if MaximizingPlayer then // for Maximizer Player
maxEva= -infinity
for each child of node do
eva= minimax(child, depth-1, alpha, beta, False)
maxEva= max(maxEva, eva)
alpha= max(alpha, maxEva)
if beta<=alpha
break
return maxEva
else // for Minimizer player
minEva= +infinity
for each child of node do
eva= minimax(child, depth-1, alpha, beta, true)
minEva= min(minEva, eva)
beta= min(beta, eva)
if beta<=alpha
break
return minEvaAlpha-Beta修剪的工作
让我们以两人搜索树为例,了解Alpha-beta修剪的工作原理
步骤1:在的第一步中,Max玩家将首先从节点A开始移动,其中节点α=-∞和β=∞,这些alpha和beta值向下传递到节点B,节点B再次是α=-∞和β=∞,而节点B将相同的值传递给其子D。
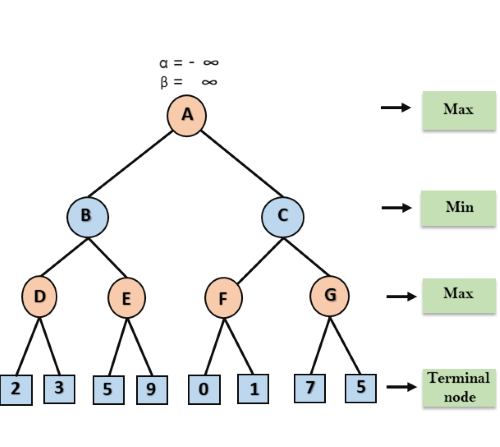
步骤2:在节点D处,将计算α的值作为其对Max的转向。首先将α的值与2进行比较,然后与3进行比较,max(2,3)= 3将是节点D处的α值,节点值也将为3。
步骤3:现在算法回溯到节点B,其中β的值将随着Min的转弯而变化,现在β=∞将与可用的后续节点值进行比较,即min(∞,3)= 3,因此现在在节点B处α=-∞,β= 3。
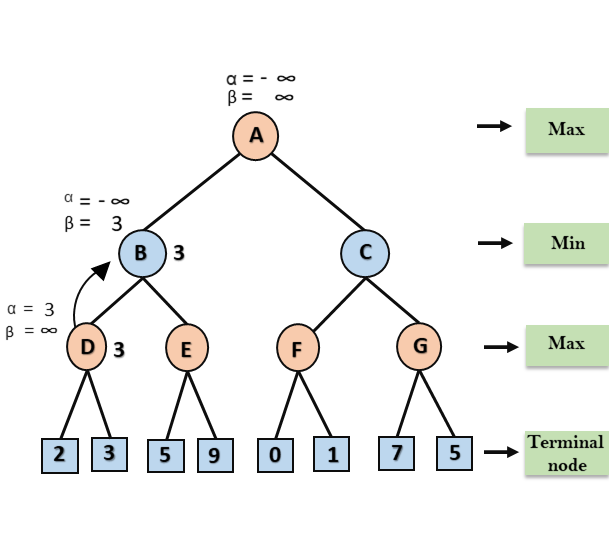
在下一步中,算法遍历节点B的下一个后继节点,即节点E,并且还将传递α=-∞和β= 3的值。
步骤4:在节点E处,Max旋转,而alpha的值将更改。 alpha的当前值将与5进行比较,因此max(-∞,5)= 5,因此在节点Eα= 5和β= 3处,其中α> =β,因此将修剪E的右后继,并且算法将不会遍历它,并且节点E处的值为5。
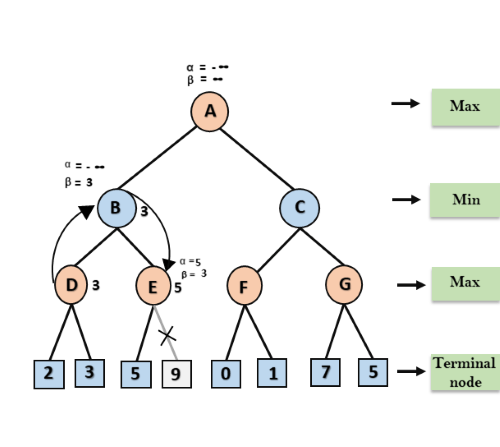
步骤5:在下一步,算法再次将树从节点B移回节点A。在节点A,将更改alpha的值,最大可用值为3,因为max(-∞,3)= 3,和β =∞,这两个值现在传递给A的右继任者,即NodeC。
在节点C处,α= 3,β=∞,并且相同的值将传递到节点F。
步骤6:在节点F处,将再次将α的值与左子代(0,max(3, 0)= 3)进行比较,然后与右子代(1,max(3, 1)=)进行比较。 3仍然α保持3,但是F的节点值将变为1。
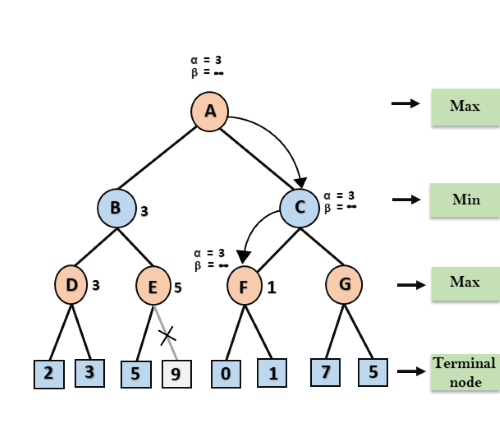
步骤7:节点F在Cα= 3和β=∞的情况下,将节点值1返回到节点C,此处β的值将被更改,它将与1比较,因此min(∞,1)= 1。 C,α= 3和β= 1,并且再次满足条件α> =β,因此将修剪C的下一个子元素G,并且该算法将不会计算整个子树G。
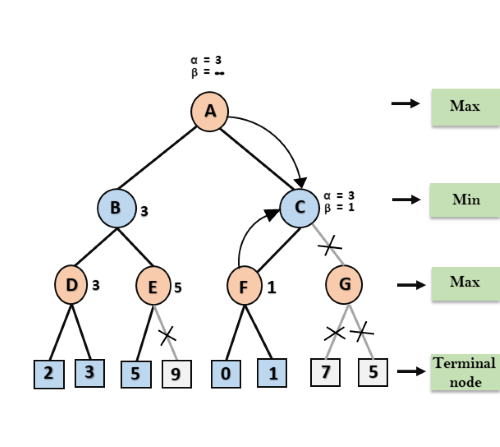
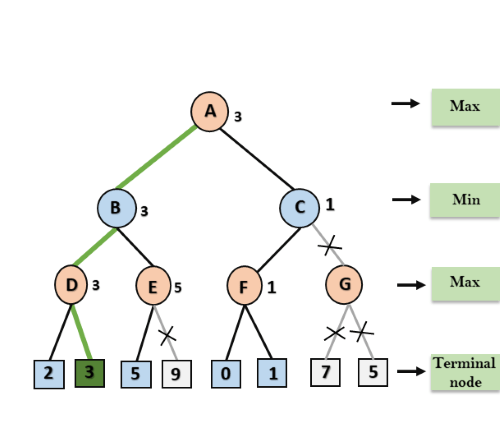
步骤8:C现在将值1返回给A,这里A的最佳值是max(3,1)=3。下面是最终的游戏树,其中显示了已计算的节点和从未计算的节点。因此,在此示例中,最大化器的最佳值为3。
Alpha-Beta修剪中的移动顺序
alpha-beta修剪的有效性高度依赖于检查每个节点的顺序。移动顺序是alpha-beta修剪的重要方面。
它可以有两种类型:
- 最坏的排序:在某些情况下,alpha-beta修剪算法不会修剪任何树上的叶子,并且与minimax算法完全一样。在这种情况下,由于α-β因素,它还会消耗更多的时间,这种修剪动作被称为最差排序。在这种情况下,最佳移动发生在树的右侧。该命令的时间复杂度为O(bm)。
- 理想的排序:当树中进行大量修剪时,α-β修剪的理想排序发生,并且最佳移动发生在树的左侧。我们应用DFS,因此它首先在树的左侧搜索,并且在相同的时间内经过两次最小深度算法。理想排序的复杂度为O(bm / 2)。
寻找良好秩序的规则
以下是在alpha-beta修剪中找到良好顺序的一些规则:
- 从最浅的节点发生最佳移动。
- 对树中的节点进行排序,以便首先检查最佳节点。
- 在寻求最佳举措的同时利用领域知识。例如:对于国际象棋,请尝试顺序:先捕获,然后威胁,然后向前移动,向后移动。
- 我们可以保留状态,因为状态可能会重复。



