本文概述
- Mini-max算法是一种递归或回溯算法,用于决策和博弈论中。假设对手也在最佳状态下进行比赛,则可为玩家提供最佳行动。
- Mini-Max算法使用递归来搜索游戏树。
- Min-Max算法主要用于AI中的游戏。例如国际象棋,西洋跳棋,井字游戏,围棋以及各种拖车游戏。该算法为当前状态计算minimax决策。
- 在这种算法中,两个玩家玩游戏,一个叫做MAX,另一个叫做MIN。
- 双方玩家都在争夺它,因为对手玩家获得的利益最小,而他们却获得了最大的利益。
- 游戏的两个玩家都是彼此的对手,其中MAX将选择最大值,而MIN将选择最小值。
- minimax算法执行深度优先搜索算法来探索完整的游戏树。
- minimax算法一直向下进行到树的终端节点,然后作为递归回溯树。
MinMax算法的伪代码
function minimax(node, depth, maximizingPlayer) is
if depth ==0 or node is a terminal node then
return static evaluation of node
if MaximizingPlayer then // for Maximizer Player
maxEva= -infinity
for each child of node do
eva= minimax(child, depth-1, false)
maxEva= max(maxEva, eva) //gives Maximum of the values
return maxEva
else // for Minimizer player
minEva= +infinity
for each child of node do
eva= minimax(child, depth-1, true)
minEva= min(minEva, eva) //gives minimum of the values
return minEva初始通话:
Minimax(node,3,true)
最小最大算法的工作
- 可以使用示例轻松描述minimax算法的工作。下面我们以代表两人游戏的游戏树为例。
- 在此示例中,有两个参与者,一个称为Maximizer,另一个称为Minimizer。
- 最大化器将尝试获得最大可能的分数,而最小化器将尝试获得最小的可能分数。
- 该算法应用了DFS,因此在此游戏树中,我们必须从头到尾一直走到终端节点。
- 在终端节点上,给出了终端值,因此我们将比较这些值并回溯树直到出现初始状态。以下是解决两人游戏树涉及的主要步骤:
步骤1:第一步,算法生成整个游戏树,并应用效用函数以获取终端状态的效用值。在下面的树图中,让我们以A为树的初始状态。假设最大化器采取第一轮,其初始值为最差=-infinity,而maximizer将采取下一轮,其初始值为最差= -infinity。
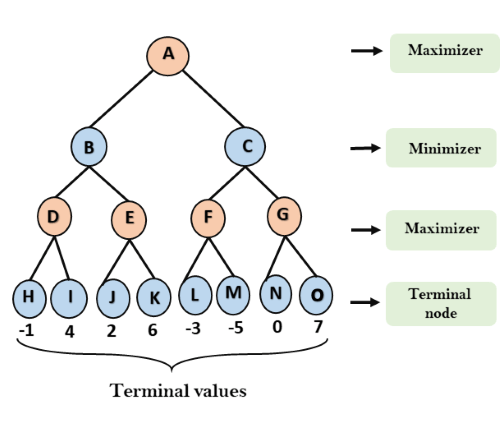
步骤2:现在,首先我们找到Maximizer的效用值,其初始值为-∞,因此我们将终端状态下的每个值与Maximizer的初始值进行比较,并确定较高的节点值。它将在所有中找到最大值。
- 对于节点D max(-1,–∞)=> max(-1, 4)= 4
- 对于节点E max(2,-∞)=> max(2,6)= 6
- 对于节点F max(-3,-∞)=> max(-3,-5)= -3
- 对于节点G max(0,-∞)= max(0,7)= 7
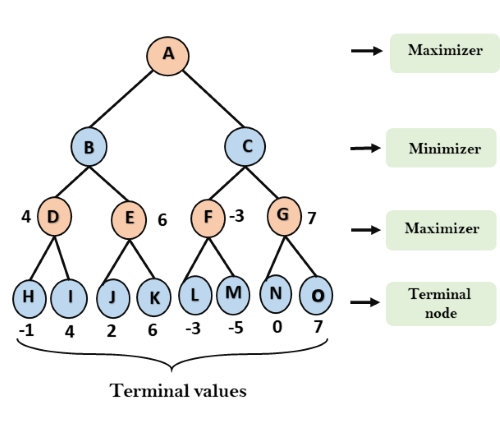
步骤3:在下一步中,轮到最小化器了,因此它将所有节点值与∞进行比较,并找到第三层节点值。
- 对于节点B =最小值(4.6)= 4
- 对于节点C =最小值(-3,7)= -3
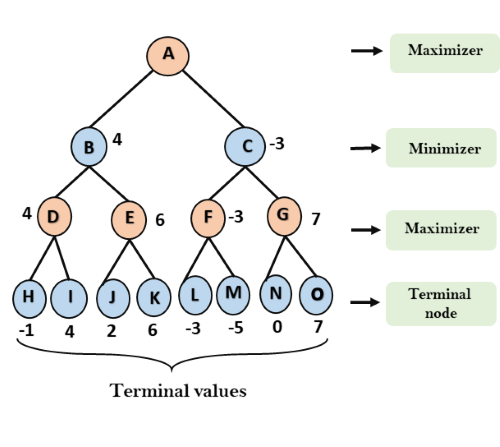
步骤3:现在轮到Maximizer了,它将再次选择所有节点的最大值,并找到根节点的最大值。在此游戏树中,只有4层,因此我们可以立即到达根节点,但在实际游戏中,将超过4层。
- 对于节点A max(4,-3)= 4
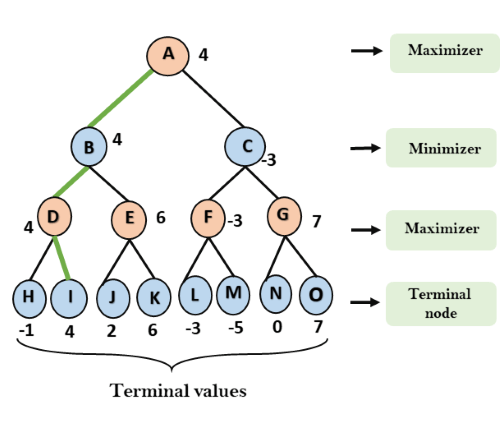
这就是minimax两人游戏的完整工作流程。
Mini-Max算法的属性
- 完成-最小-最大算法已完成。它肯定会在有限搜索树中找到一个解决方案(如果存在)。
- 如果两个对手的比赛都达到最佳状态,则Optimal-Min-Max算法是最佳方案。
- 时间复杂度-由于它对游戏树执行DFS,因此Min-Max算法的时间复杂度为O(bm),其中b是游戏树的分支因子,m是树的最大深度。
- 空间复杂度-Mini-max算法的空间复杂度也类似于DFS,即O(bm)。
minimax算法的局限性
minimax算法的主要缺点是,对于复杂的游戏(如国际象棋,围棋等),它的运行速度非常慢。这种类型的游戏具有很大的分支因子,并且玩家可以选择很多选择。 minimax算法的这一局限性可以通过我们在下一个主题中讨论的alpha-beta修剪得到改善。



