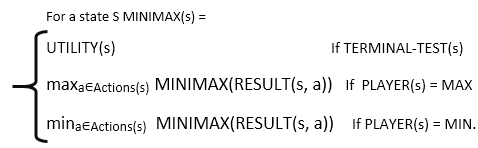本文概述
对抗性搜索是一种搜索,我们在其中研究当我们尝试超前计划而其他代理商正在针对我们进行计划时出现的问题。
- 在先前的主题中,我们研究了仅与单个代理相关联的搜索策略,该代理旨在查找通常以一系列动作形式表示的解决方案。
- 但是,在某些情况下,可能会有多个代理在同一搜索空间中搜索解决方案,并且这种情况通常发生在游戏中。
- 具有多个代理的环境称为多代理环境,其中每个代理都是其他代理的对手并相互竞争。每个代理都需要考虑其他代理的行为以及该行为对其绩效的影响。
- 因此,两个或两个以上目标冲突的玩家试图为解决方案探索相同搜索空间的搜索称为对抗搜索,通常称为游戏。
- 游戏被建模为搜索问题和启发式评估功能,这是有助于在AI中建模和解决游戏的两个主要因素。
人工智能中的游戏类型
| 确定性 | 机会移动 | |
|---|---|---|
| 完美信息 | 国际象棋, 跳棋, 奥赛罗 | 步步高, 垄断 |
| 信息不完善 | 战舰, 盲目, 井字游戏 | 桥梁, 扑克, 拼字游戏, 核战争 |
- 完美信息:具有完美信息的游戏是代理商可以观察整个董事会的信息。特工拥有有关游戏的所有信息,并且他们也可以看到彼此的动作。例如国际象棋,跳棋,围棋等。
- 信息不完善:如果在游戏中代理商没有掌握有关游戏的所有信息,也不了解发生了什么情况,则这类游戏称为信息不完善的游戏,例如井字游戏,战舰,盲人,桥牌,等等
- 确定性游戏:确定性游戏是那些遵循严格的游戏模式和规则的游戏,并且没有随机性。例如国际象棋,跳棋,围棋,井字游戏等。
- 非确定性游戏:非确定性游戏是那些具有各种不可预测事件并具有机会或运气因素的游戏。骰子或纸牌会引入这种机会或运气因素。这些是随机的,每个动作的响应都不是固定的。这样的游戏也称为随机游戏。示例:西洋双陆棋,大富翁,扑克等
注意:在本主题中,我们将讨论确定性博弈,完全可观察的环境,零和以及每个代理交替执行的操作。
零和博弈
- 零和游戏是对抗性搜索,其中涉及纯粹的竞争。
- 在零和博弈中,每个代理的效用得失由另一个代理的效用得失精确平衡。
- 游戏中的一位玩家尝试使一个单一值最大化,而另一位玩家尝试使一个单一值最小化。
- 游戏中一位玩家的每一步称为合股。
- 象棋和井字游戏是零和游戏的例子。
零和博弈:嵌入式思维
零和游戏涉及嵌入式思维,其中一位特工或玩家试图找出:
- 该怎么办。
- 如何决定举动
- 还需要考虑他的对手
- 对手也想怎么做
每个玩家都试图找出对手对他们的行为的反应。这需要嵌入式思维或后向推理来解决AI中的游戏问题。
问题的形式化:
可以将游戏定义为AI中的一种搜索类型,可以将以下元素形式化:
- 初始状态:指定开始时的游戏设置。
- 玩家:它指定哪个玩家在状态空间中移动。
- 行动(一个或多个):它返回状态空间中的一组合法移动。
- 结果(s,a):这是过渡模型,指定状态空间中的移动结果。
- 终端测试:如果游戏结束,终端测试为true,否则无论如何都为false。游戏结束的状态称为终端状态。
- 效用(s,p):效用函数给出游戏的最终数值,该游戏的最终状态为玩家p的终端状态s。也称为支付功能。对于国际象棋,结果是赢,输或平,其收益值为1、0、1 / 2。对于井字游戏,效用值为1,-1和0。
游戏树
游戏树是一棵树,其中树的节点是游戏状态,树的边缘是玩家的移动。游戏树涉及初始状态,动作功能和结果功能。
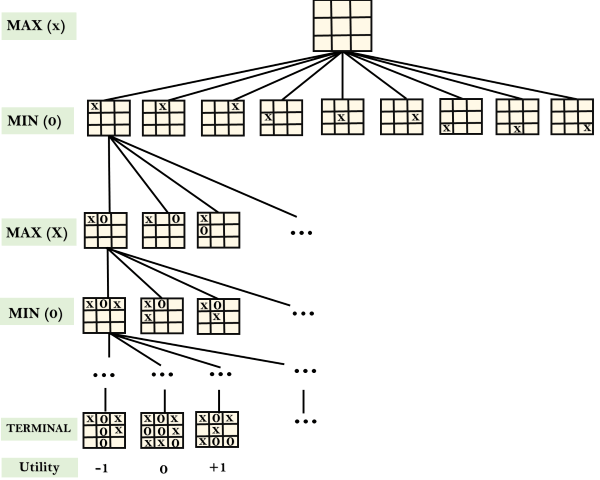
示例:井字游戏树:
下图显示了井字游戏的游戏树的一部分。以下是游戏的一些重点:
- 有两名球员最大和最小。
- 玩家有另一回合,并从MAX开始。
- MAX最大化游戏树的结果
- MIN使结果最小化。
示例说明:
- 从初始状态开始,MAX首先开始有9个可能的动作。 MAX位置X和MIN位置O,然后两个玩家交替玩,直到我们到达一个叶子节点,其中一个参与者连续三个,或者所有正方形都填满。
- 双方都将计算每个节点的最小值,最大值,最小值,这是针对最佳对手的最佳可实现效用。
- 假设两个玩家都非常清楚井字游戏并发挥出最佳状态。每个玩家都在尽力防止另一个玩家获胜。 MIN在游戏中与Max对抗。
- 因此,在游戏树中,我们有一个Max层,一个MIN层,每一层称为Ply。 Max放置x,然后MIN放置o来阻止Max获胜,此游戏将继续进行到终端节点。
- MIN赢了,MAX赢了,或者是平局。此游戏树是MIN和MAX玩井字游戏并交替轮流的可能性的整个搜索空间。
因此,对抗性搜索maxmax程序的工作方式如下:
- 它旨在找到MAX赢得比赛的最佳策略。
- 它遵循深度优先搜索的方法。
- 在游戏树中,最佳叶子节点可以出现在树的任何深度。
- 将minimax值传播到树,直到发现终端节点。
在给定的游戏树中,可以从每个节点的最小值最大值(可以写为MINIMAX(n))确定最佳策略。 MAX更喜欢移至最大值状态,而MIN更喜欢移至最小值状态,然后: