本文概述
到目前为止,我们已经讨论了不知情的搜索算法,该算法通过搜索空间寻找问题的所有可能解决方案,而无需任何其他有关搜索空间的知识。但是,明智的搜索算法包含一系列知识,例如我们距目标有多远,路径成本,如何到达目标节点等。这些知识可帮助代理减少对搜索空间的探索,并更有效地找到目标节点。
信息搜索算法对于较大的搜索空间更有用。知情搜索算法使用启发式的思想,因此也称为启发式搜索。
启发式功能:启发式功能是在知情搜索中使用的功能,它找到了最有前途的路径。它以业务代表的当前状态作为其输入,并根据目标得出对业务代表的亲密程度的估计。但是,启发式方法可能并不总是提供最佳解决方案,但可以保证在合理的时间内找到一个好的解决方案。启发式函数估计状态与目标的接近程度。它由h(n)表示,并计算状态对之间最佳路径的成本。启发式函数的值始终为正。
启发式函数的可容许性为:
h(n) <= h*(n)此处,h(n)是启发式成本,而h *(n)是估计成本。因此,启发式成本应小于或等于估计成本。
纯启发式搜索
纯粹的启发式搜索是启发式搜索算法的最简单形式。它根据节点的启发式值h(n)扩展节点。它维护两个列表,OPEN和CLOSED列表。在“已关闭”列表中,它将放置已扩展的节点,在“打开”列表中,将放置尚未扩展的节点。
在每次迭代中,具有最低启发式值的每个节点n都会展开并生成其所有后继节点,并且n会放置在封闭列表中。该算法继续以找到目标状态为单位。
在知情的搜索中,我们将讨论以下两种主要算法:
- 最佳优先搜索算法(贪婪搜索)
- A *搜索算法
1.)最佳优先搜索算法(贪婪搜索):
贪婪的最佳优先搜索算法始终会选择此时出现的最佳路径。它是深度优先搜索算法和广度优先搜索算法的结合。它使用启发式功能和搜索。最佳优先搜索使我们能够利用两种算法的优势。借助最佳优先搜索,我们可以在每个步骤中选择最有前途的节点。在最好的优先搜索算法中,我们扩展最接近目标节点的节点,并通过启发式函数(即启发式函数)估算最近的成本。
f(n)= g(n).h(n)=从节点n到目标的估计成本。
贪婪的最佳第一算法是由优先级队列实现的。
最佳优先搜索算法:
- 步骤1:将起始节点放入OPEN列表中。
- 步骤2:如果“打开”列表为空,则停止并返回失败。
- 步骤3:从OPEN列表中删除具有最低h(n)值的节点n,并将其放在CLOSED列表中。
- 步骤4:展开节点n,并生成节点n的后继者。
- 步骤5:检查节点n的每个后继节点,并确定是否有任何节点是目标节点。如果任何后继节点是目标节点,则返回成功并终止搜索,否则继续执行步骤6。
- 步骤6:对于每个后继节点,算法将检查评估函数f(n),然后检查该节点是否处于“打开”或“关闭”列表中。如果该节点不在两个列表中,则将其添加到OPEN列表中。
- 步骤7:返回步骤2。
优点:
- 通过获得两种算法的优势,最佳的优先搜索可以在BFS和DFS之间切换。
- 该算法比BFS和DFS算法更有效。
缺点:
- 在最坏的情况下,它可以充当无向导的深度优先搜索。
- 它可能像DFS一样陷入循环。
- 此算法不是最佳算法。
例:
考虑以下搜索问题,我们将使用贪婪的最佳优先搜索遍历它。在每次迭代时,使用下表中给出的评估函数f(n)= h(n)扩展每个节点。
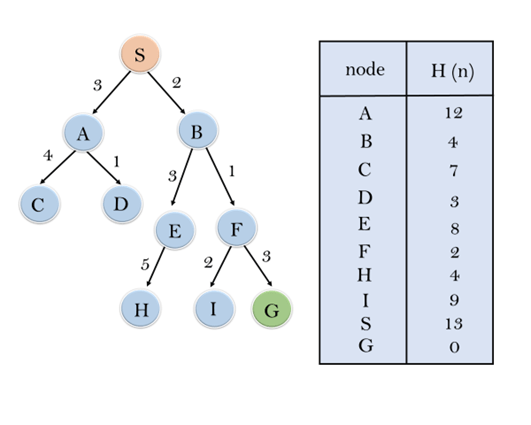
在此搜索示例中,我们使用两个列表,即“打开”列表和“关闭”列表。以下是遍历以上示例的迭代。
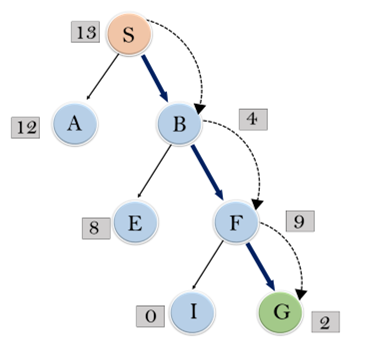
展开S的节点并放入CLOSED列表
初始化:打开[A,B],关闭[S]
迭代1:打开[A],关闭[S,B]
迭代2:打开[E,F,A],关闭[S,B]:打开[E,A],关闭[S,B,F]
迭代3:打开[I,G,E,A],关闭[S,B,F]:打开[I,E,A],关闭[S,B,F,G]
因此,最终的解决方案路径为:S —-> B —–> F —-> G
时间复杂度:贪婪最佳优先搜索的最坏情况时间复杂度为O(bm)。
空间复杂度:贪婪最佳优先搜索的最坏情况下的空间复杂度是O(bm)。其中,m是搜索空间的最大深度。
完全:即使给定的状态空间是有限的,贪婪的最佳第一搜索也是不完整的。
最佳:贪婪的最佳优先搜索算法不是最佳的。
2.)A *搜索算法:
A *搜索是最佳优先搜索的最普遍形式。它使用启发式函数h(n)和从起始状态g(n)到达节点n的成本。它结合了UCS和贪婪的最佳优先搜索功能,可以有效地解决问题。 A *搜索算法使用启发式函数查找通过搜索空间的最短路径。该搜索算法扩展了较少的搜索树,并更快地提供了最佳结果。 A *算法与UCS类似,不同之处在于它使用g(n)h(n)代替g(n)。
在A *搜索算法中,我们使用搜索启发式方法以及到达节点的成本。因此,我们可以将以下两种成本进行合并,该总和称为适应度数。
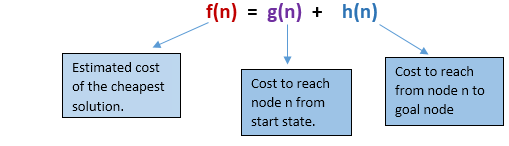
在搜索空间的每个点上,只有那些具有最低f(n)值的节点才会展开,并且算法在找到目标节点时终止。
A *搜索算法:
步骤1:将起始节点放在OPEN列表中。
步骤2:检查OPEN列表是否为空,如果列表为空,则返回失败并停止。
步骤3:从OPEN列表中选择评估函数值最小的节点(g h),如果节点n是目标节点,则返回成功并停止,否则
步骤4:展开节点n并生成其所有后继节点,然后将n放入封闭列表中。对于每个后继n’,检查n’是否已在OPEN或CLOSED列表中,如果不是,则计算n’的评估函数并放入Open列表中。
步骤5:否则,如果节点n’已经处于OPEN和CLOSED状态,则应将其附加到反映最低g(n’)值的后指针。
步骤6:返回步骤2。
优点:
- 与其他搜索算法相比,A *搜索算法是最佳算法。
- A *搜索算法是最佳且完整的。
- 该算法可以解决非常复杂的问题。
缺点:
- 它并不总是产生最短的路径,因为它主要基于启发式算法和近似值。
- A *搜索算法存在一些复杂性问题。
- A *的主要缺点是内存需求,因为它会将所有生成的节点都保留在内存中,因此对于各种大规模问题不切实际。
例:
在本例中,我们将使用A*算法遍历给定的图。下表给出了所有状态的启发式值,我们将使用公式f(n)= g(n) + h(n)计算每个状态的f(n),其中g(n)是到达任意节点的起始状态的代价。
这里我们将使用开列表和闭列表。

解:

初始化:{(S,5)}
迭代1:{(S-> A,4),(S-> G,10)}
迭代2:{(S-> A-> C,4),(S-> A-> B,7),(S-> G,10)}
迭代3:{(S-> A-> C —> G,6),(S-> A-> C —> D,11),(S-> A-> B,7),(S-> G,10)}
迭代4将给出最终结果,因为S —> A —> C —> G提供了成本为6的最佳路径。
要记住的要点:
- A *算法返回最先出现的路径,并且不搜索所有剩余路径。
- A *算法的效率取决于启发式算法的质量。
- A *算法扩展满足条件f(n)的所有节点
完成:只要满足以下条件,A *算法即已完成:
- 分支因子是有限的。
- 每次行动的费用是固定的。
最佳:如果满足以下两个条件,则A *搜索算法是最佳的:
- 可允许的:最优性的第一个条件是h(n)应该是A *树搜索的可允许启发式。可允许的启发式方法本质上是乐观的。
- 一致性:第二个必要条件是仅A *图形搜索的一致性。
如果启发式函数是允许的,则A *树搜索将始终找到成本最低的路径。
时间复杂度:A *搜索算法的时间复杂度取决于启发式函数,并且扩展的节点数与解的深度d成指数关系。因此,时间复杂度为O(b ^ d),其中b是分支因子。
空间复杂度:A *搜索算法的空间复杂度为O(b ^ d)



