毕达哥拉斯四重奏详细介绍

本文概述

• C ++
• Java
• Python3
• C#
• 的PHP

给定4分, 检查它们是否构成勾股四重奏。

它定义为整数a, b, c, d的元组, 使得

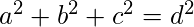
。它们基本上是丢番图方程的解。在几何解释中，它表示边长为整数的长方体|a|， |b|， |c|，其空间对角线为|d|。

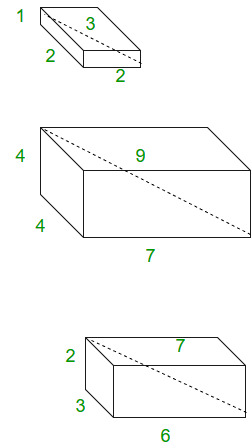
此处显示的长方体侧面是毕达哥拉斯四联体的示例。

当它们的最大公约数为1时, 它是原始的。每个勾股四边形都是原始四边形的整数倍。我们可以生成一组原始的毕达哥拉斯四联体, 对于它们, a可以通过公式生成：

a = m2 + n2 – p2 – q2, b = 2(mq + np), c = 2(nq – mp), d = m2 + n2 + p2 + q2

其中m, n, p, q是最大公约数为1的非负整数, 因此m + n + p + q为奇数。因此, 所有原始毕达哥拉斯四联体的特征是勒贝格的身份.

(m2 + n2 + p2 + q2)2 =(2mq + 2nq)2 + 2(nq – mp)2 +(m2 + n2 – p2 – q2)m2 + n2 – p2 – q2

C ++

//C++ code to detect Pythagorean Quadruples.
#include <bits/stdc++.h>
using namespace std;
  
//function for checking
bool pythagorean_quadruple( int a, int b, int c, int d)
{
     int sum = a * a + b * b + c * c;
     if (d * d == sum)
         return true ;
     else
         return false ;
}
  
//Driver Code
int main()
{
     int a = 1, b = 2, c = 2, d = 3;
     if (pythagorean_quadruple(a, b, c, d))
         cout <<"Yes" <<endl;
     else
         cout <<"No" <<endl;
}

Java

//Java code to detect Pythagorean Quadruples.
import java.io.*;
import java.util.*;
  
class GFG {
  
//function for checking
static Boolean pythagorean_quadruple( int a, int b, int c, int d)
{
     int sum = a * a + b * b + c * c;
     if (d * d == sum)
         return true ;
     else
         return false ;
}
  
//Driver function
     public static void main (String[] args) {
     int a = 1 , b = 2 , c = 2 , d = 3 ;
     if (pythagorean_quadruple(a, b, c, d))
         System.out.println( "Yes" );
     else
         System.out.println( "No" );
          
     }
}
//This code is contributed by Gitanjali.

Python3

# Python  code to detect
# Pythagorean Quadruples.
import math
  
# function for checking
def pythagorean_quadruple(a, b, c, d):
  
     sum = a * a + b * b + c * c;
     if (d * d = = sum ):
         return True
     else :
         return False
  
#driver code
a = 1
b = 2
c = 2
d = 3
if (pythagorean_quadruple(a, b, c, d)):
     print ( "Yes" )
else :
      print ( "No" )
  
# This code is contributed
# by Gitanjali.

C#

//C# code to detect 
//Pythagorean Quadruples.
using System;
  
class GFG {
  
     //function for checking
     static Boolean pythagorean_quadruple( int a, int b, int c, int d)
     {
         int sum = a * a + b * b + c * c;
         if (d * d == sum)
             return true ;
         else
             return false ;
     }
      
     //Driver function
         public static void Main () {
              
         int a = 1, b = 2, c = 2, d = 3;
          
         if (pythagorean_quadruple(a, b, c, d))
             Console.WriteLine( "Yes" );
         else
             Console.WriteLine( "No" );
              
     }
}
  
//This code is contributed by vt_M.

的PHP

<?php
//php code to detect Pythagorean Quadruples.
  
//function for checking
function pythagorean_quadruple( $a , $b , $c , $d )
{
     $sum = $a * $a + $b * $b + $c * $c ;
      
     if ( $d * $d == $sum )
         return true;
     else
         return false;
}
  
//Driver Code
     $a = 1; $b = 2; $c = 2; $d = 3;
      
     if (pythagorean_quadruple( $a , $b , $c , $d ))
         echo "Yes" ;
     else
         echo "No" ;
          
//This code is contributed by anuj_67.
?>

输出如下：

Yes

参考文献

维基：https://en.wikipedia.org/wiki/Pythagorean_quadruple

数学世界：http://mathworld.wolfram.com/PythagoreanQuadruple.html

---