毕达哥拉斯定理是一个著名的定理, 也是一个非常古老的定理。毕达哥拉斯定理为我们提供了直角三角形中边之间的关系。直角三角形由两条腿和一条斜边组成。两条腿以90°角相交, 斜边是直角三角形的最长边, 是与直角相反的边。
在直角三角形中, 斜边的平方等于其他两侧的平方之和。
毕达哥拉斯定理的公式
考虑下面给出的三角形, 其中” a”是垂直边, ” b”是底边, ” c”是斜边, 然后根据定义, 毕达哥拉斯定理公式为:
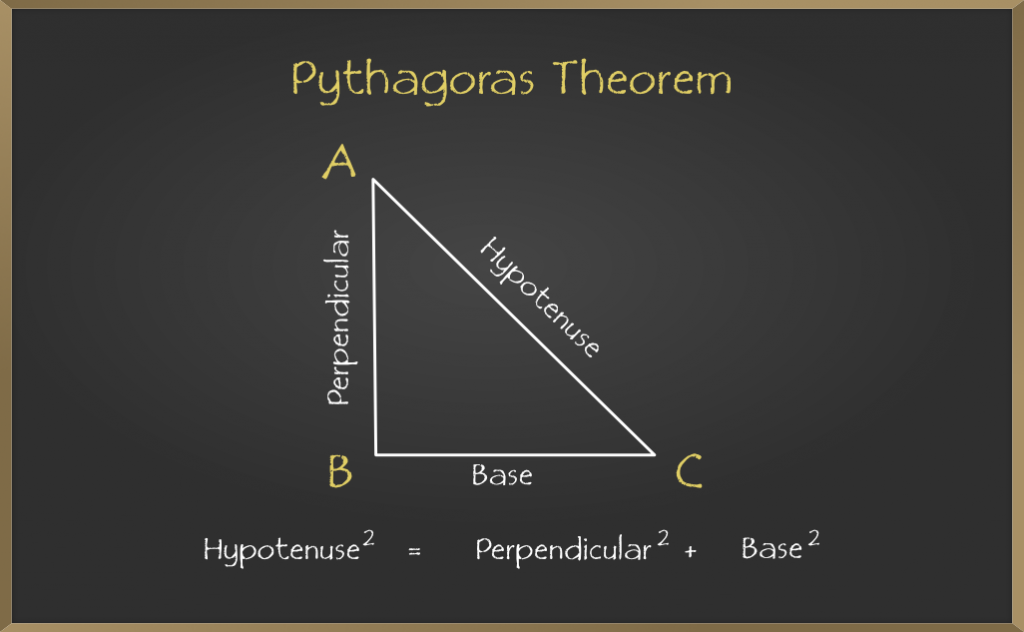
毕达哥拉斯定理的证明
让我们看一下传统的证明毕达哥拉斯定理公式的方法, 该公式表示斜边上的正方形面积等于两个较短边上的正方形面积之和。下图显示了在每边绘制的正方形。
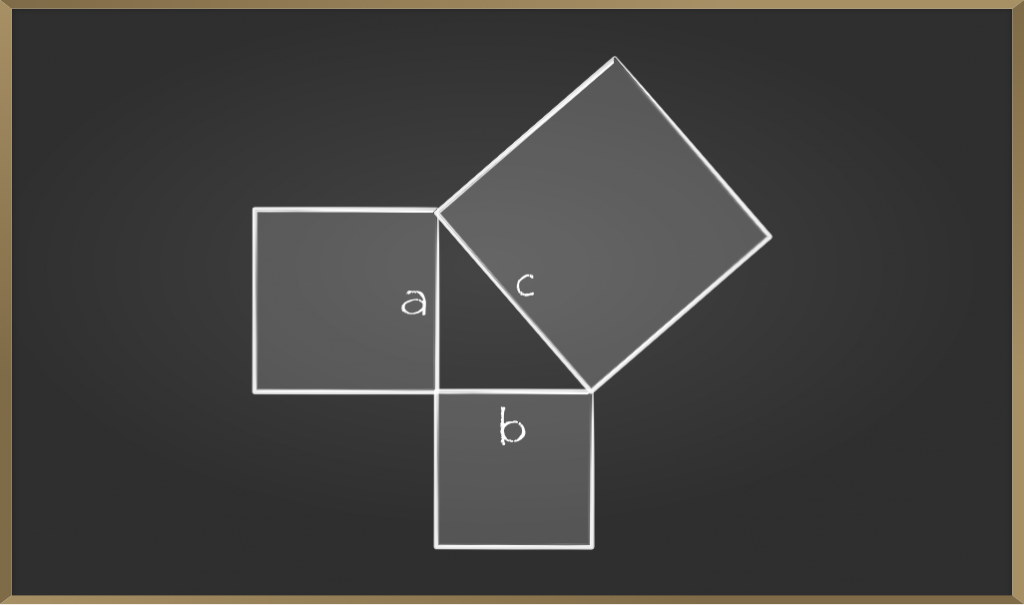
考虑分别安装在三角形A, B和C的三个边上的边a, b, c的三个正方形。
毕达哥拉斯定理:
正方形A的面积+正方形B的面积=正方形C的面积
那不过是
一种2+ b2= c2
现在, 让我们解决一些问题, 以更好地理解该概念。
毕达哥拉斯定理的样本问题
问题1:在下面给定的直角三角形中找到y的值。
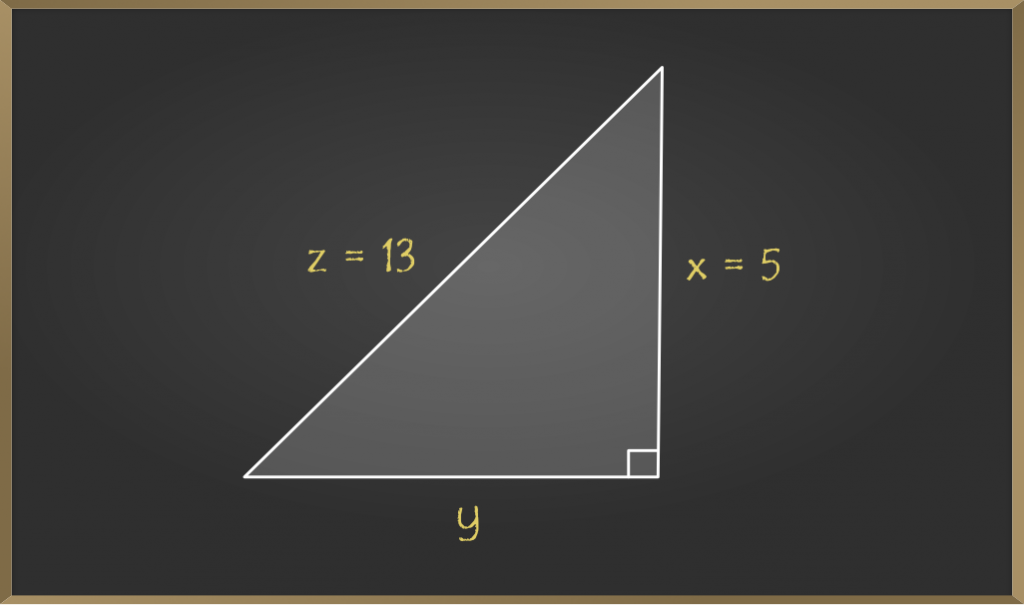
解:
通过毕达哥拉斯定理的陈述, 我们得到=> z2 = x2 + y2
现在, 直接替换值, 我们得到== 132 = 52 + y2 => 169 = 25 + y2 => y2 = 144 => y =√ 144 = 12
问题2: 给定一个矩形, 长度为4厘米, 宽度为3厘米。找到矩形的对角线长度?
解:

在上图中, 矩形的长度为4厘米, 宽度为3厘米。
现在我们必须找到点A到点C或点B到点D的距离。两者都给出相同的答案, 因为相对的边长相同, 即AC++= BD
现在, 我们通过画一条假想线找到A点和C点之间的距离。
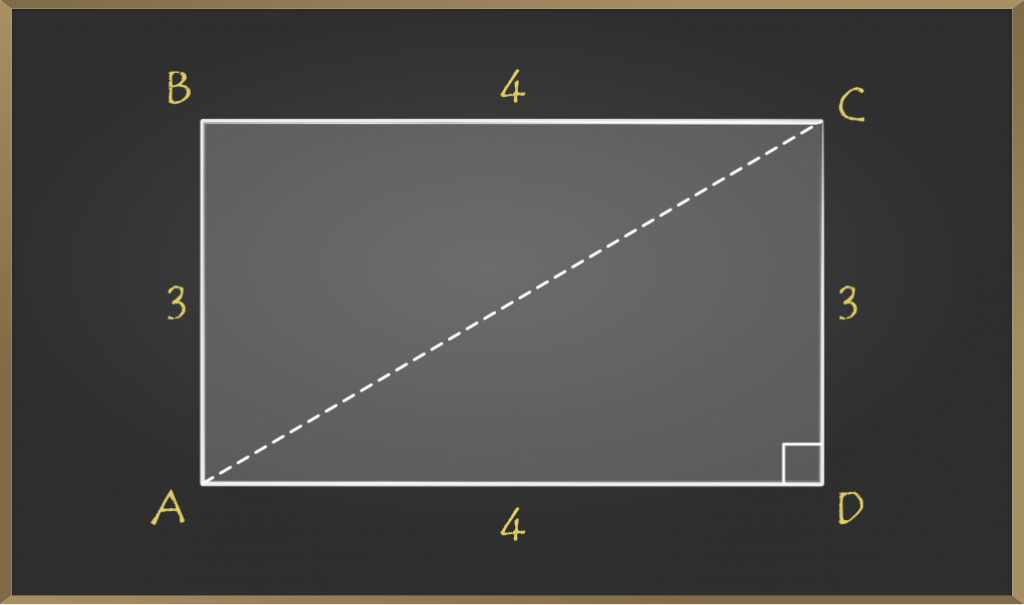
现在, 三角形ACD是直角三角形。因此, 根据毕达哥拉斯定理, => AC2 = AD2 + CD2 => AC2 = 42 + 32 => AC2 = 25 => AC++=√25= 5因此, 给定矩形的对角线长度为5 cm。
毕达哥拉斯定理的逆
毕达哥拉斯定理的反义词与毕达哥拉斯定理非常相似。要理解该定理, 你应该从毕达哥拉斯定理的反面进行思考。
如果三角形最长边的长度的平方等于其他两个边的平方和, 则该三角形为直角三角形。
毕达哥拉斯逆定理的公式和证明
该公式将与毕达哥拉斯定理的相反部分相同。根据该陈述, 我们需要证明情况发生, 然后三角形应为直角三角形, 因为我们需要证明最长边的对角应为90°。
如果存在一个长度为a, b和c的三角形
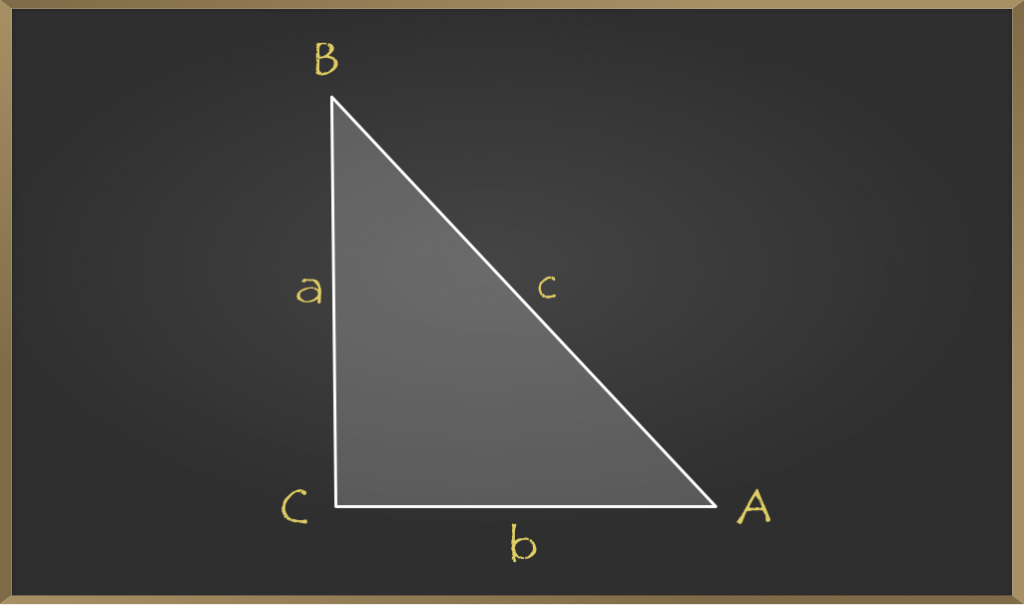
我们假设它满足C2=一个2+ b2通过查看该图可以知道∠C= 90°, 但要证明这一点, 我们需要另一个三角形△EGF, 例如AC++= EG = b和BC++= FG = a。
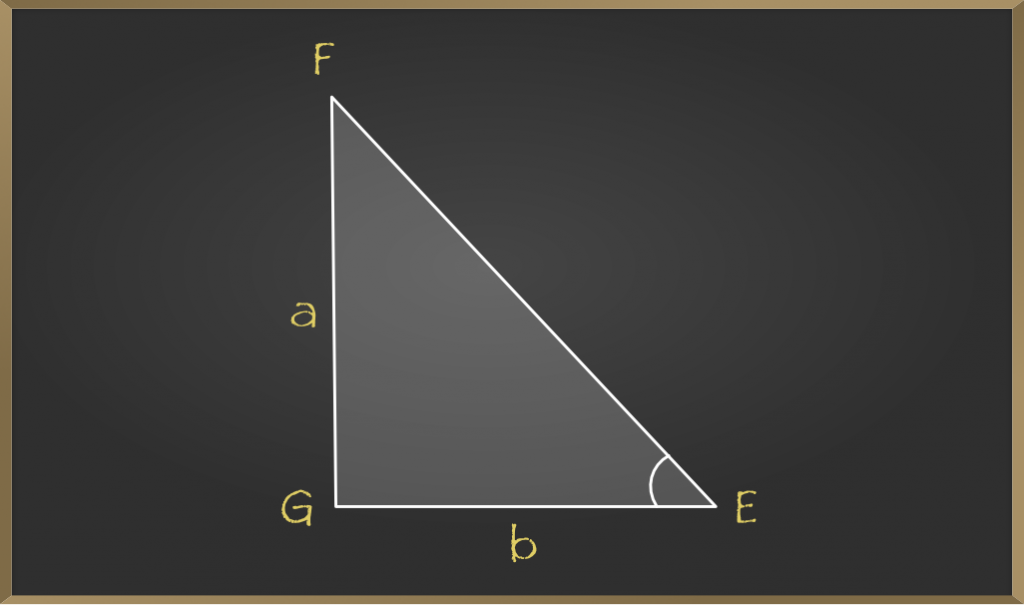
在△EGF中, 毕达哥拉斯定理:=> EF2 = EG2 + FG22 = b2 + a2…………(1)在△ABC中, 毕达哥拉斯定理:=> AB2 = AC2 + BC2 = b2 + a2…………( 2)从等式(1)和(2), 我们得到; => EF2 = AB2 => EF = AB =>△ACB≅△EGF(通过SSS假设)=>∠G是直角
因此, △EGF是直角三角形。
因此, 可以说勾股定理的逆也成立。
毕达哥拉斯定理逆的样本问题
问题1:三角形的边是5、12和13。检查给定的三角形是否是直角三角形?
解:
鉴于
=> a = 5 => b = 12 => c = 13通过使用勾股定理的反函数, => a2 + b2 = c2替换上式中的给定值, => 132 = 52 + 122 => 169 = 25 + 144 => 169 = 169因此, 给定的长度满足上述条件。因此, 给定的三角形是直角三角形。
问题2: 三角形的边长为9厘米, 11厘米和6厘米。这个三角形是直角三角形吗?如果是这样, 斜边是哪一边?
解:
我们知道斜边是最长的一面。如果9 cm, 11 cm和6 cm是该成角度的三角形的长度, 则11 cm将成为斜边。
使用毕达哥拉斯定理的逆, 我们得到
=>(11)2 =(9)2 +(6)2 => 121 = 81 + 36 => 121≠117
由于两边不相等, 因此9 cm, 11 cm和6 cm不是直角三角形的边。




