每一个计算机科学的初学者都曾经想过为什么我们要在图中找到最短路径或者树有什么用,我们要用环链表来玩约瑟夫斯圈吗?
因此,本文将讨论数据结构和算法在现实世界中的重要性,以参考COVID-19。
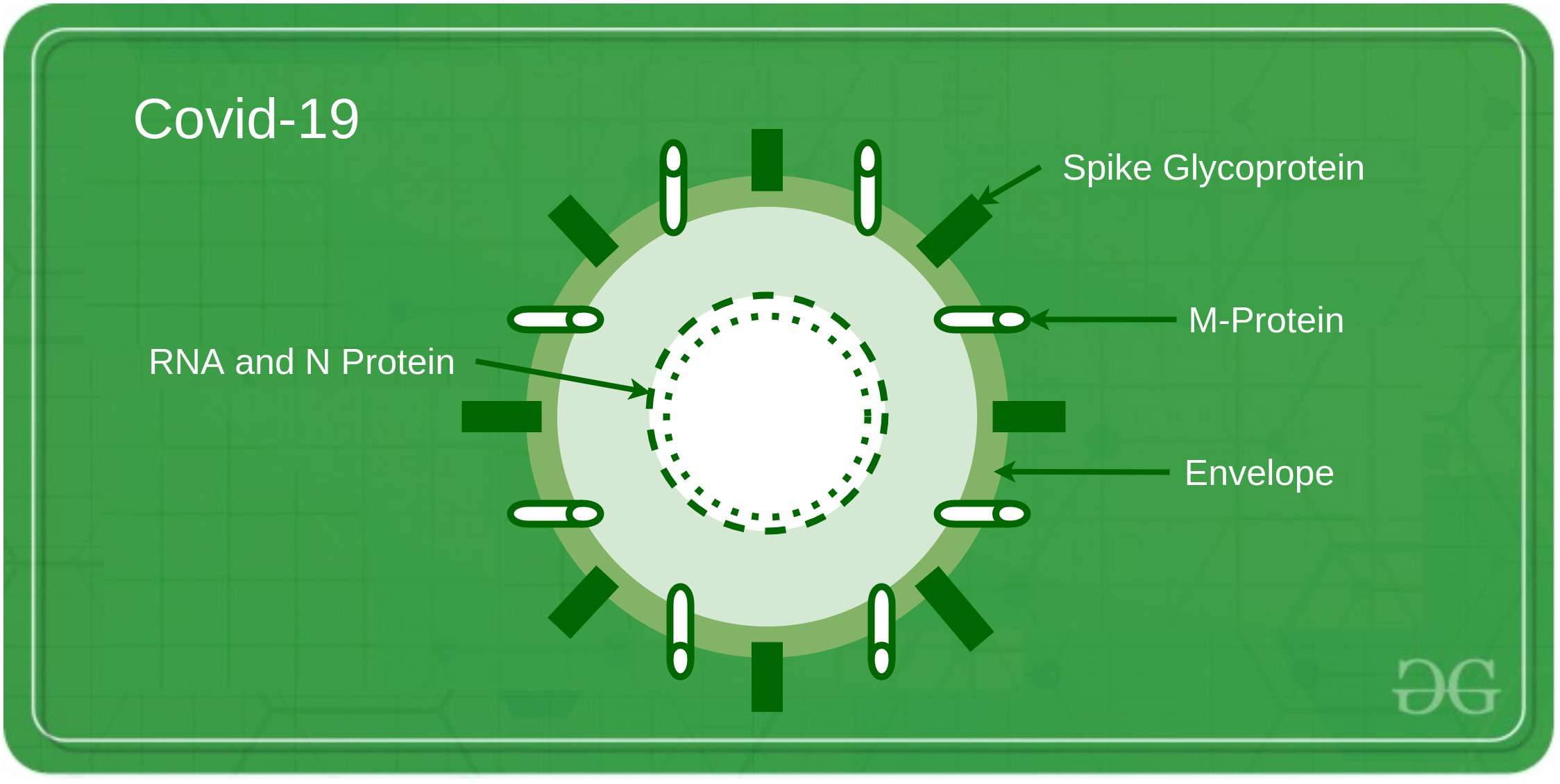
目前被称为COVID-19的冠状病毒急性呼吸道疾病暴发已导致重大流行病。冠状病毒成为主要问题的主要原因是因为它的传播可以用树来建模。
据估计, 在世界采取封锁措施之前, 每个感染者正在感染另外2-4个人。这个数字叫做R0(R-naught), 一种数学表示, 表示传染病的传染性。例如, 如果疾病具有R0在15岁以下的人中, 有这种疾病的人会平均将其传播给15个人。
取决于疾病的R, 存在三种传播或减少疾病的可能性0值:
- 如果R0小于1, 则每个现有感染导致少于一个新感染。在这种情况下, 疾病最终将消亡。
- 如果R0等于1, 则每个现有感染都会导致一个新感染。该疾病将继续存活并稳定下来, 但不会爆发。
- 如果R0大于1, 则每个现有感染都会导致一个以上新感染。该疾病将被传播, 并可能爆发或流行。
重要的是, 疾病的R0仅当人群中的每个人都完全容易感染该疾病时才适用此值, 例如在COVID-19的情况下, 没有人接种过疫苗, 以前没有人患过该病, 也没有办法控制该病的传播。
在我们的模型中,R0是树中每个节点的平均子节点数。这意味着——树中的每个节点(平均)有2到4个子节点。
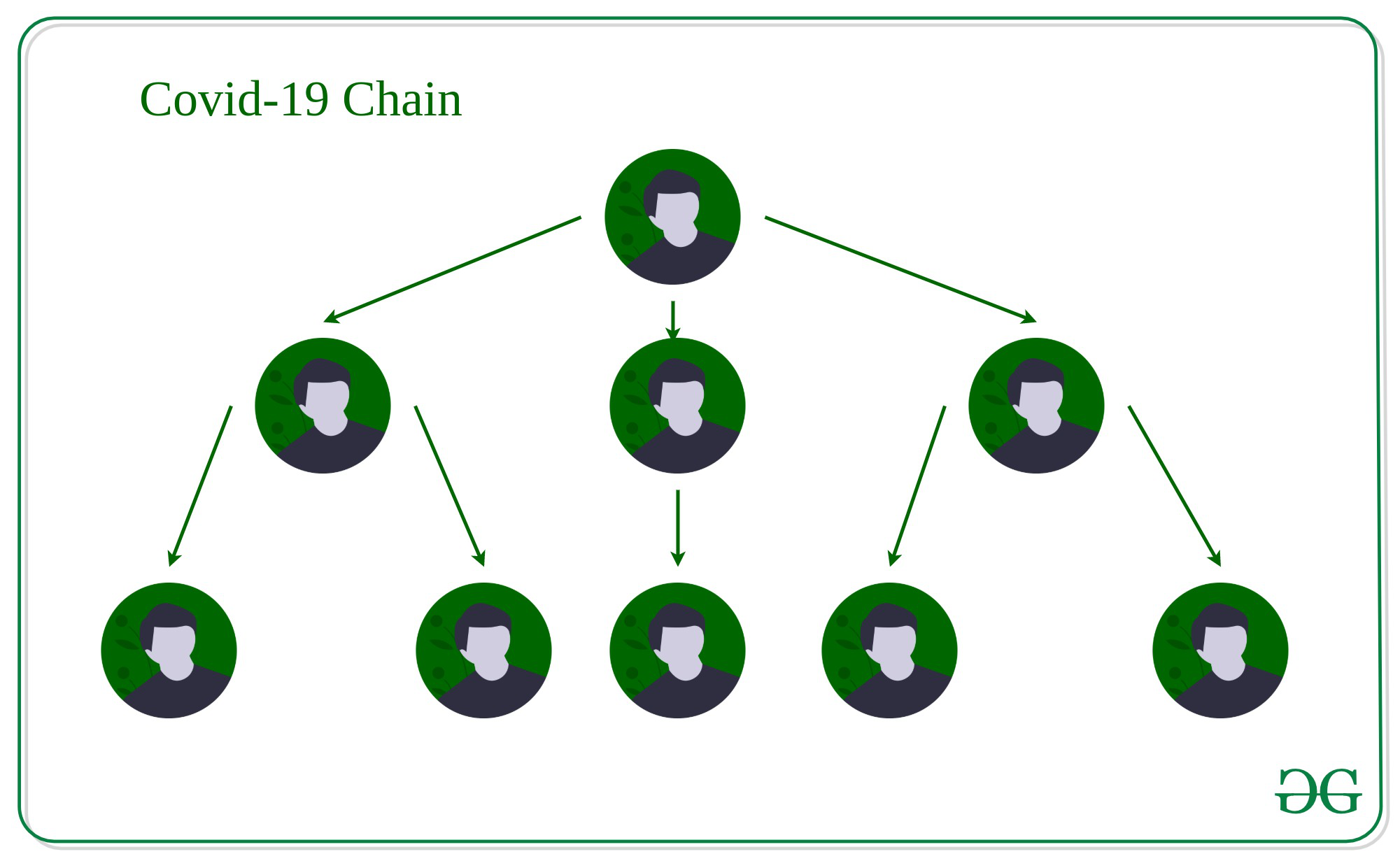
如果你对树木进行了任何深度的研究, 你都会知道它会变得非常大, 非常快。
世界卫生组织的早期目标是将R0减少到1左右(或更少)。如果R0= 1,那么树中的每个叶节点现在都成为链表的头。每个人都恰好感染另一个人,就像(单个)链表引用链表中的下一个节点一样。
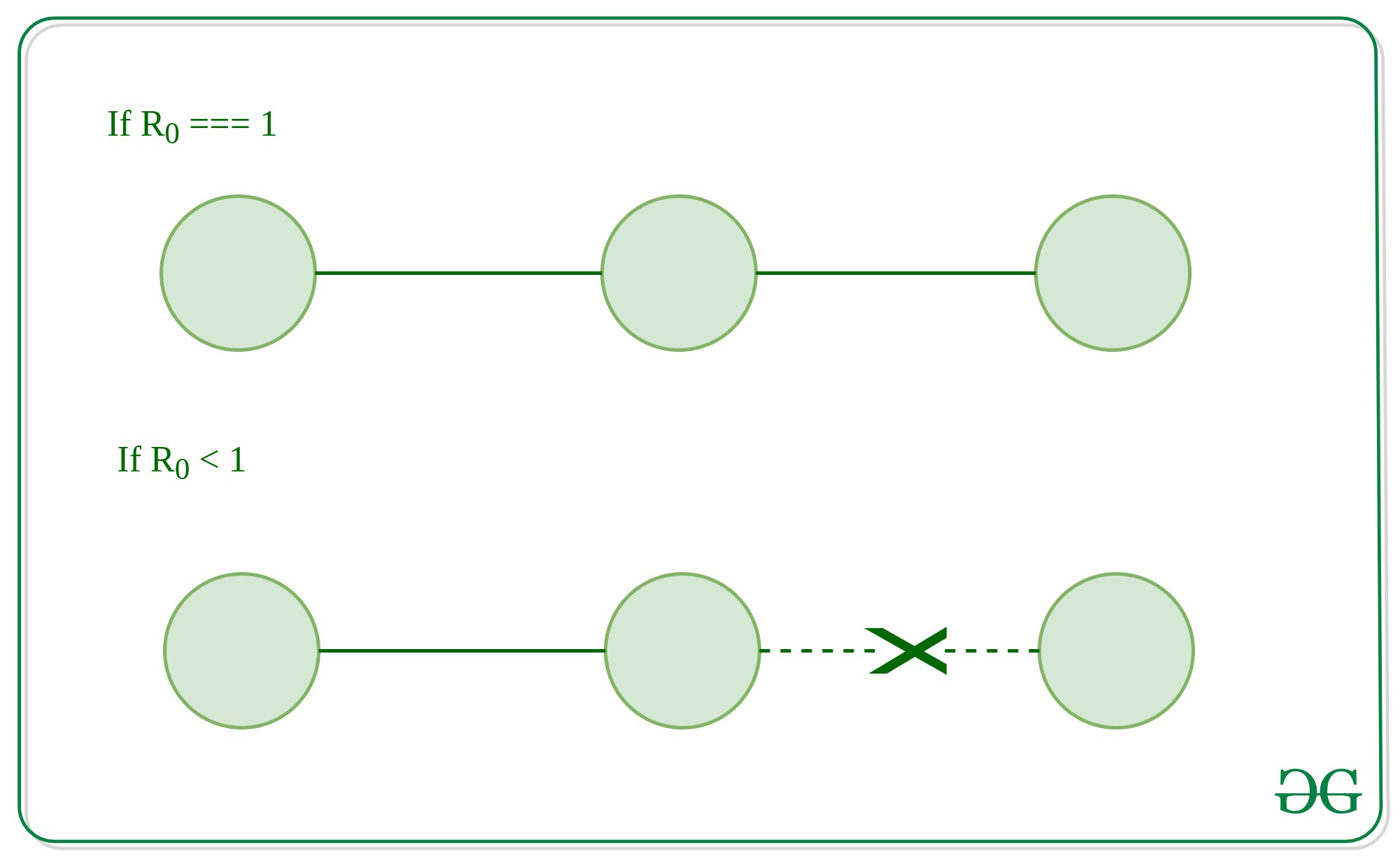
如果R0<1, 那么在某个时候, 一个人将没有另一个人被感染, 并且感染线(对于那片叶子)被破坏了。我们可以通过使节点指向空引用来在代码中进行建模, 这意味着它是链表中的最终节点。
解决冠状病毒情况的一种方法是更改病毒的行为, 以便可以通过(最终是有限的)链接列表(而不是树)的集合对其进行建模。树木, 图表&链表不仅用于法昂访谈, 但实际上对于建模和解决现实世界中的现象非常有用。
因此, 请保持安全并留在内部, 以打破电晕病毒链。




