本文概述
斐波那契三角形或Hosoya三角形是基于斐波那契数的三角形排列。每个数字都是上面左对角线或右对角线上两个数字的和。前几行是:

这个三角形中的数字遵循递归关系
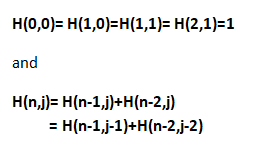
与斐波那契数的关系
三角形中的条目满足标识
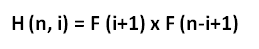
因此,最外面的两条对角线是斐波那契数,而中间垂直线上的数字是斐波那契数的平方。三角形中所有其他的数都是两个不同的大于1的斐波那契数的乘积。行和是第一个卷积的斐波那契数。
stackoverflow:https://stackoverflow.com/questions/36275039/create-a-hosoyas-triangle-in-java
维基百科:https://en.wikipedia.org/wiki/Hosoya%27s_triangle
给定一个整数n,任务是打印Hosoya的大小为n的三角形。
例子:
Input : n = 4
Output :
1
1 1
2 1 2
3 2 2 3
Input : n = 5
Output :
1
1 1
2 1 2
3 2 2 3
5 3 4 3 5下面是打印Hosoya的高度为n的三角形的实现:
C ++
// CPP Program to print Hosoya's
// triangle of height n.
#include <bits/stdc++.h>
using namespace std;
int Hosoya( int n, int m)
{
// Base case
if ((n == 0 && m == 0) ||
(n == 1 && m == 0) ||
(n == 1 && m == 1) ||
(n == 2 && m == 1))
return 1;
// Recursive step
if (n > m)
return Hosoya(n - 1, m)
+ Hosoya(n - 2, m);
else if (m == n)
return Hosoya(n - 1, m - 1)
+ Hosoya(n - 2, m - 2);
else
return 0;
}
// Print the Hosoya triangle of height n.
void printHosoya( int n)
{
for ( int i = 0; i < n; i++) {
for ( int j = 0; j <= i; j++)
cout << Hosoya(i, j) << " " ;
cout << endl;
}
}
// Driven Program
int main()
{
int n = 5;
printHosoya(n);
return 0;
}Java
// Java Program to print Hosoya's
// triangle of height n.
import java.util.*;
class GFG {
static int Hosoya( int n, int m)
{
// Base case
if ((n == 0 && m == 0 ) ||
(n == 1 && m == 0 ) ||
(n == 1 && m == 1 ) ||
(n == 2 && m == 1 ))
return 1 ;
// Recursive step
if (n > m)
return Hosoya(n - 1 , m)
+ Hosoya(n - 2 , m);
else if (m == n)
return Hosoya(n - 1 , m - 1 )
+ Hosoya(n - 2 , m - 2 );
else
return 0 ;
}
// Print the Hosoya triangle of height n.
static void printHosoya( int n)
{
for ( int i = 0 ; i < n; i++)
{
for ( int j = 0 ; j <= i; j++)
System.out.print(Hosoya(i, j)
+ " " );
System.out.println( "" );
}
}
/* Driver program to test above function */
public static void main(String[] args)
{
int n = 5 ;
printHosoya(n);
}
}
// This code is contributed by Arnav Kr. Mandal.Python3
# Python3 code to print Hosoya's
# triangle of height n.
def Hosoya( n , m ):
# Base case
if ((n = = 0 and m = = 0 ) or
(n = = 1 and m = = 0 ) or
(n = = 1 and m = = 1 ) or
(n = = 2 and m = = 1 )):
return 1
# Recursive step
if n > m:
return Hosoya(n - 1 , m)
+ Hosoya(n - 2 , m)
elif m = = n:
return Hosoya(n - 1 , m - 1 )
+ Hosoya(n - 2 , m - 2 )
else :
return 0
# Print the Hosoya triangle of height n.
def printHosoya( n ):
for i in range (n):
for j in range (i + 1 ):
print (Hosoya(i, j) , end = " " )
print ( "\n" , end = "")
# Driven Code
n = 5
printHosoya(n)
# This code is contributed by Sharad_BhardwajC#
// C# Program to print Hosoya's
// triangle of height n.
using System;
class GFG {
static int Hosoya( int n, int m)
{
// Base case
if ((n == 0 && m == 0) ||
(n == 1 && m == 0) ||
(n == 1 && m == 1) ||
(n == 2 && m == 1))
return 1;
// Recursive step
if (n > m)
return Hosoya(n - 1, m)
+ Hosoya(n - 2, m);
else if (m == n)
return Hosoya(n - 1, m - 1)
+ Hosoya(n - 2, m - 2);
else
return 0;
}
// Print the Hosoya triangle of height n.
static void printHosoya( int n)
{
for ( int i = 0; i < n; i++)
{
for ( int j = 0; j <= i; j++)
Console.Write(Hosoya(i, j)
+ " " );
Console.WriteLine( "" );
}
}
/* Driver program to test above function */
public static void Main()
{
int n = 5;
printHosoya(n);
}
}
// This code is contributed by vt_m.的PHP
<?php
// PHP Program to print Hosoya's
// triangle of height n.
function Hosoya(int $n , int $m )
{
// Base case
if (( $n == 0 && $m == 0) ||
( $n == 1 && $m == 0) ||
( $n == 1 && $m == 1) ||
( $n == 2 && $m == 1))
return 1;
// Recursive step
if ( $n > $m )
return Hosoya( $n - 1, $m ) +
Hosoya( $n - 2, $m );
else if ( $m == $n )
return Hosoya( $n - 1, $m - 1) +
Hosoya( $n - 2, $m - 2);
else
return 0;
}
// Print the Hosoya
// triangle of height n.
function printHosoya( $n )
{
for ( $i = 0; $i < $n ; $i ++)
{
for ( $j = 0; $j <= $i ; $j ++)
echo Hosoya( $i , $j ) , " " ;
echo "\n" ;
}
}
// Driven Code
$n = 5;
printHosoya( $n );
// This code is contributed by anuj_67.
?>输出:
1
1 1
2 1 2
3 2 2 3
5 3 4 3 5下面是使用动态编程打印高度为n的Hosoya三角形的实现:
C ++
// CPP Program to print Hosoya's triangle of height n.
#include <bits/stdc++.h>
#define N 5
using namespace std;
// Print the Hosoya triangle of height n.
void printHosoya( int n)
{
int dp[N][N];
memset (dp, 0, sizeof (dp));
// base case.
dp[0][0] = dp[1][0] = dp[1][1] = 1;
// For each row.
for ( int i = 2; i < n; i++) {
// for each column;
for ( int j = 0; j < n; j++) {
// recursive steps.
if (i > j)
dp[i][j] = dp[i - 1][j] + dp[i - 2][j];
else
dp[i][j] = dp[i - 1][j - 1] + dp[i - 2][j - 2];
}
}
// printing the solution
for ( int i = 0; i < n; i++) {
for ( int j = 0; j <= i; j++)
cout << dp[i][j] << " " ;
cout << endl;
}
}
// Driven Program
int main()
{
int n = 5;
printHosoya(n);
return 0;
}Java
// JAVA Code for Hosoya Triangle
import java.util.*;
class GFG {
static int N = 5 ;
// Print the Hosoya triangle
// of height n.
static void printHosoya( int n)
{
int dp[][] = new int [N][N];
// base case.
dp[ 0 ][ 0 ] = dp[ 1 ][ 0 ] = 1 ;
dp[ 1 ][ 1 ] = 1 ;
// For each row.
for ( int i = 2 ; i < n; i++)
{
// for each column;
for ( int j = 0 ; j < n; j++)
{
// recursive steps.
if (i > j)
dp[i][j] = dp[i - 1 ][j] +
dp[i - 2 ][j];
else
dp[i][j] = dp[i - 1 ][j - 1 ] +
dp[i - 2 ][j - 2 ];
}
}
// printing the solution
for ( int i = 0 ; i < n; i++)
{
for ( int j = 0 ; j <= i; j++)
System.out.print(dp[i][j] + " " );
System.out.println( "" );
}
}
/* Driver program*/
public static void main(String[] args)
{
int n = 5 ;
printHosoya(n);
}
}
// This code is contributed by Arnav Kr. Mandal.Python3
# Python3 Program to print
# Hosoya's triangle of height n.
N = 5
# Print the Hosoya triangle
# of height n.
def printHosoya(n):
dp = [[ 0 for i in range (N)]
for i in range (N)]
# base case.
dp[ 0 ][ 0 ] = dp[ 1 ][ 0 ] = dp[ 1 ][ 1 ] = 1
# For each row.
for i in range ( 2 , n):
# for each column
for j in range (n):
# recursive steps.
if (i > j):
dp[i][j] = (dp[i - 1 ][j] +
dp[i - 2 ][j])
else :
dp[i][j] = (dp[i - 1 ][j - 1 ] +
dp[i - 2 ][j - 2 ])
# printing the solution
for i in range (n):
for j in range (i + 1 ):
print (dp[i][j], end = ' ' )
print ()
# Driver Code
n = 5
printHosoya(n)
# This code is contributed
# by sahilshelangiaC#
// C# Code for Hosoya Triangle
using System;
class GFG {
static int N = 5;
// Print the Hosoya triangle
// of height n.
static void printHosoya( int n)
{
int [, ]dp = new int [N, N];
// base case.
dp[0, 0] = dp[1, 0] = 1;
dp[1, 1] = 1;
// For each row.
for ( int i = 2; i < n; i++)
{
// for each column;
for ( int j = 0; j < n; j++)
{
// recursive steps.
if (i > j)
dp[i, j] = dp[i - 1, j] +
dp[i - 2, j];
else
dp[i, j] = dp[i - 1, j - 1]
+ dp[i - 2, j - 2];
}
}
// printing the solution
for ( int i = 0; i < n; i++)
{
for ( int j = 0; j <= i; j++)
Console.Write(dp[i, j] + " " );
Console.WriteLine( "" );
}
}
/* Driver program*/
public static void Main()
{
int n = 5;
printHosoya(n);
}
}
// This code is contributed by Vt_m.的PHP
<?php
// PHP Program to print Hosoya's triangle of height n.
$N =5;
// Print the Hosoya triangle of height n.
function printHosoya( $n )
{
global $N ;
$dp = array_fill (0, $N , array_fill (0, $N , 0));
// base case.
$dp [0][0] = $dp [1][0] = $dp [1][1] = 1;
// For each row.
for ( $i = 2; $i < $n ; $i ++) {
// for each column;
for ( $j = 0; $j < $n ; $j ++) {
// recursive steps.
if ( $i > $j )
$dp [ $i ][ $j ] = $dp [ $i - 1][ $j ]
+ $dp [ $i - 2][ $j ];
else
$dp [ $i ][ $j ] = $dp [ $i - 1][ $j - 1]
+ $dp [ $i - 2][ $j - 2];
}
}
// printing the solution
for ( $i = 0; $i < $n ; $i ++) {
for ( $j = 0; $j <= $i ; $j ++)
echo $dp [ $i ][ $j ]. " " ;
echo "\n" ;
}
}
// Driven Program
$n = 5;
printHosoya( $n );
// This code is contributed by mits
?>输出:
1
1 1
2 1 2
3 2 2 3
5 3 4 3 5



