一个匹配项二部图是一组边的选择方式, 没有两个边共享一个端点。最大匹配是最大大小(最大边数)的匹配。在最大匹配中, 如果添加了任何边缘, 则不再是匹配。给定的二分图可能有多个以上的最大匹配项。
我们已经讨论了最大匹配和基于福特富尔克森的最大二分匹配方法in以前的帖子。基于福特福尔克森算法的时间复杂度为O(V x E)。
Hopcroft Karp算法是对O(√Vx E)时间的改进。在讨论算法之前, 让我们定义几个术语
自由节点或顶点:给定匹配M, 不属于匹配的节点称为自由节点。最初, 所有顶点都是免费的(请参见下图的第一个图)。在第二张图中, u2和v2是空闲的。在第三张图中, 没有顶点是自由的。
匹配边缘和非匹配边缘:给定匹配的M, 作为匹配的一部分的边缘称为”匹配边缘”, 不属于M的边缘(或连接自由节点)的边缘称为”非匹配”边缘。在第一个图中, 所有边都不匹配。在第二张图中, (u0, v1), (u1, v0)和(u3, v3)匹配, 其他不匹配。
替代路径:在给定匹配M的情况下, 交替路径是其中边缘可替换地属于匹配而不匹配的路径。所有单边路径均为交替路径。中间图中交替路径的示例是u0-v1-u2和u2-v1-u0-v2。
增强路径:给定匹配的M, 增广路径是从自由顶点开始和结束的交替路径。以自由顶点开始和结束的所有单边路径都是扩充路径。在下图中, 增强路径以蓝色突出显示。请注意, 扩展路径始终具有一个额外的匹配边。
Hopcroft Karp算法基于以下概念。
如果存在扩展路径, 则匹配M不是最大值。其他方法也是如此, 即如果不存在扩展路径, 则匹配为最大
因此, 想法是一一寻找扩展路径。并将找到的路径添加到当前匹配项。
Hopcroft Karp算法
1) Initialize Maximal Matching M as empty.
2) While there exists an Augmenting Path p
Remove matching edges of p from M and add not-matching edges of p to M
(This increases size of M by 1 as p starts and ends with a free vertex)
3) Return M.下图显示了该算法的工作。
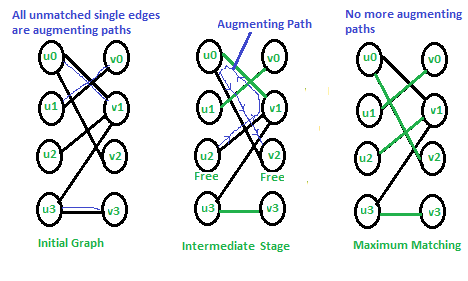
在初始图中, 所有单个边都是增加路径, 我们可以按任意顺序进行选择。在中间阶段, 只有一条扩展路径。我们从M中删除此路径的匹配边, 并添加不匹配边。在最终匹配中, 没有扩展路径, 因此匹配最大。
集合2中讨论了Hopcroft Karp算法的实现。
Hopcroft–Karp最大匹配算法S2(实现)
参考文献:
https://en.wikipedia.org/wiki/Hopcroft%E2%80%93Karp_algorithm
http://www.dis.uniroma1.it/~leon/tcs/lecture2.pdf
如果发现任何不正确的地方, 或者想分享有关上述主题的更多信息, 请发表评论。




