证明:-Clique是否是NPC?
为此, 你必须满足以下几点:-
- clique
- 3CNF≤ρclique
- clique≤ρ3CNF≤SAT
- cliqueϵNP
1)clique
定义:-在“群体”中, 每个顶点都直接连接到另一个顶点, 并且“群体”中的顶点数量代表“群体”的大小。
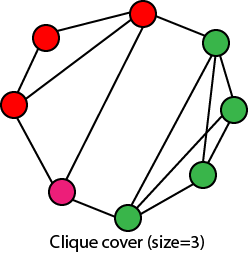
CLIQUE COVER:-给定一个图G和一个整数k, 我们能否找到顶点V1, V2 … VK的k个子集, 使得UiVi = V, 并且每个Vi是G的一个集团。
下图显示了一个图形, 其大小为3。
2)3CNF≤ρclique
证明:-要成功地从3CNF转换为Clique, 你必须遵循以下两个步骤:-
以顶点的形式绘制子句, 每个顶点代表子句的文字。
- 他们不相辅相成
- 它们不属于同一子句。在转换中, Clique的大小和3CNF的大小必须相同, 并且你已在多项式时间内成功将3CNF转换为Clique
clique≤ρ3CNF
证明:-如你所知, K子句的函数必须存在大小为k的集团。这意味着来自不同子句的P个变量可以分配相同的值(例如为1)。通过使用CLIQUES的所有变量的这些值, 可以使函数中每个子句的值等于1
示例:-在3CNF中有一个布尔函数:-
(X + Y + Z)(X + Y + Z’)(X + Y’+ Z)
从3CNF还原/转换为CLIQUE后, 你将获得P变量, 例如:-x + y = 1, x + z = 1和x = 1
将P变量的值放在方程式(i)中
(1+1+0)(1+0+0)(1+0+1)
(1)(1)(1)= 1输出已验证
4)单击ϵ NP:-
证明:-如你所知, 你可以通过3CNF获得集团, 并将基于决策的NP问题转换为3CNF, 你必须首先转换为SAT, 而SAT来自NP。
因此, 得出CLIQUE属于NP的结论。
NPC证明:
- 在从3CNF到Clique的多项式时间内实现的约简
- 并验证了从Clique还原到3CNF以上后的输出, 因此得出结论, 如果还原和验证都可以在多项式时间内完成, 这意味着Clique在NPC中也是如此。




