解决单个最短路径问题, 其中边权重可能为负, 但不存在负循环。
当有向图G的某些边缘可能具有负权重时, 此算法正确运行。当没有负重量的循环时, 我们可以找出源与目标之间的最短路径。
它比Dijkstra的算法慢, 但功能更多, 因为它能够处理一些负重量边缘。
该算法检测图中的负循环并报告其存在。
基于“松弛原理”, 其中更精确的值逐渐将近似值恢复到适当的距离, 直到最终达到最佳解。
给定具有源s和权重函数w:E→R的加权有向图G =(V, E), Bellman-Ford算法返回一个布尔值, 该布尔值指示是否有可从源获得的负权重周期。如果存在这样的循环, 该算法将产生最短的路径及其权重。当且仅当图形不包含负数(可从源到达的权重循环)时, 算法才返回TRUE。
递归关系
distk [u] = [min [distk-1 [u], min [distk-1 [i] + cost [i, u]]]], 除u外。
k→k是源顶点u→u是目标顶点i→有关该顶点要扫描的边数。
BELLMAN -FORD (G, w, s)
1. INITIALIZE - SINGLE - SOURCE (G, s)
2. for i ← 1 to |V[G]| - 1
3. do for each edge (u, v) ∈ E [G]
4. do RELAX (u, v, w)
5. for each edge (u, v) ∈ E [G]
6. do if d [v] > d [u] + w (u, v)
7. then return FALSE.
8. return TRUE.示例:首先, 我们列出所有边缘及其权重。
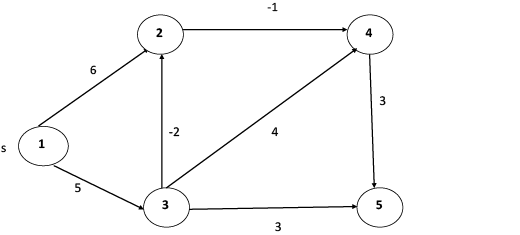
解:
distk [u] = [min [distk-1 [u], min [distk-1 [i] + cost [i, u]]]], i≠u。
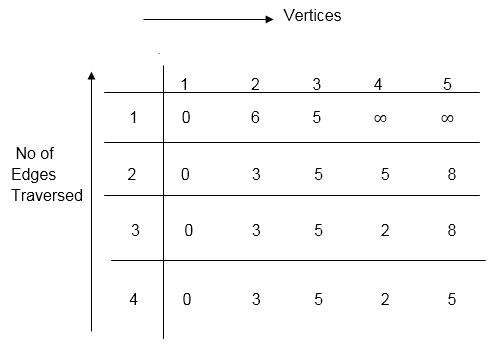
dist2 [2] = min [dist1 [2], min [dist1 [1] + cost [1, 2], dist1 [3] + cost [3, 2], dist1 [4] + cost [4, 2], dist1 [5] + cost [5, 2]]]
最小值= [6, 0 + 6, 5 +(-2), ∞+∞, ∞+∞] = 3
dist2 [3] = min [dist1 [3], min [dist1 [1] + cost [1, 3], dist1 [2] + cost [2, 3], dist1 [4] + cost [4, 3], dist1 [5] + cost [5, 3]]]
最小值= [5, 0 +∞, 6 +∞, ∞+∞, ∞+∞] = 5
dist2 [4] = min [dist1 [4], min [dist1 [1] + cost [1, 4], dist1 [2] + cost [2, 4], dist1 [3] + cost [3, 4], dist1 [5] + cost [5, 4]]]
最小值= [∞, 0 +∞, 6 +(-1), 5 + 4, ∞+∞] = 5
dist2 [5] = min [dist1 [5], min [dist1 [1] + cost [1, 5], dist1 [2] + cost [2, 5], dist1 [3] + cost [3, 5], dist1 [4] + cost [4, 5]]]
最小值= [∞, 0 +∞, 6 +∞, 5 + 3, ∞+ 3] = 8
dist3 [2] = min [dist2 [2], min [dist2 [1] + cost [1, 2], dist2 [3] + cost [3, 2], dist2 [4] + cost [4, 2], dist2 [5] + cost [5, 2]]]
最小值= [3, 0 + 6, 5 +(-2), 5 +∞, 8 +∞] = 3
dist3 [3] = min [dist2 [3], min [dist2 [1] + cost [1, 3], dist2 [2] + cost [2, 3], dist2 [4] + cost [4, 3], dist2 [5] + cost [5, 3]]]
最小值= [5, 0 +∞, 3 +∞, 5 +∞, 8 +∞] = 5
dist3 [4] = min [dist2 [4], min [dist2 [1] + cost [1, 4], dist2 [2] + cost [2, 4], dist2 [3] + cost [3, 4], dist2 [5] + cost [5, 4]]]
最小值= [5, 0 +∞, 3 +(-1), 5 + 4, 4, 8 +∞] = 2
dist3 [5] = min [dist2 [5], min [dist2 [1] + cost [1, 5], dist2 [2] + cost [2, 5], dist2 [3] + cost [3, 5], dist2 [4] + cost [4, 5]]]
最小值= [8, 0 +∞, 3 +∞, 5 + 3, 5 + 3] = 8
dist4 [2] = min [dist3 [2], min [dist3 [1] + cost [1, 2], dist3 [3] + cost [3, 2], dist3 [4] + cost [4, 2], dist3 [5] + cost [5, 2]]]
最小值= [3, 0 + 6, 5 +(-2), 2 +∞, 8 +∞] = 3
dist4 [3] = min [dist3 [3], min [dist3 [1] + cost [1, 3], dist3 [2] + cost [2, 3], dist3 [4] + cost [4, 3], dist3 [5] + cost [5, 3]]]
最小值= 5, 0 +∞, 3 +∞, 2 +∞, 8 +∞] = 5
dist4 [4] = min [dist3 [4], min [dist3 [1] + cost [1, 4], dist3 [2] + cost [2, 4], dist3 [3] + cost [3, 4], dist3 [5] + cost [5, 4]]]
最小值= [2, 0 +∞, 3 +(-1), 5 + 4, 4, 8 +∞] = 2
dist4 [5] = min [dist3 [5], min [dist3 [1] + cost [1, 5], dist3 [2] + cost [2, 5], dist3 [3] + cost [3, 5], dist3 [5] + cost [4, 5]]]
最小值= [8, 0 +∞, 3 +∞, 8, 5] = 5




