它是一种贪心算法, 可以解决有向图G =(V, E)具有非负边权重, 即每个边(u, v)∈E w(u, v)≥0的有向图的单源最短路径问题。
Dijkstra的算法会维护一组顶点S, 这些顶点的最终最短路径权重已确定。这是针对所有顶点v∈S;我们有d [v] =δ(s, v)。该算法反复选择具有最小最短路径估计的顶点u∈V-S, 将u插入S并放宽所有留下u的边。
因为它总是选择V-S中“最轻”或“最接近”的顶点插入集合S中, 所以称为贪心策略。
Dijkstra's Algorithm (G, w, s)
1. INITIALIZE - SINGLE - SOURCE (G, s)
2. S←∅
3. Q←V [G]
4. while Q ≠ ∅
5. do u ← EXTRACT - MIN (Q)
6. S ← S ∪ {u}
7. for each vertex v ∈ Adj [u]
8. do RELAX (u, v, w)分析:Dijkstra算法在具有边E和顶点V的图形上的运行时间可以表示为| E |的函数。和| V |使用Big-O表示法。 Dijkstra算法的最简单实现是将集合Q的顶点存储在普通链表或数组中, 而Extract-Min(Q)操作只是对Q中所有顶点的线性搜索。在这种情况下, 运行时间为O(| V2 | + | E | = O(V2)。
例:
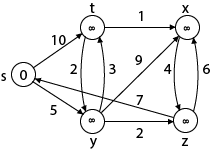
解:
步骤1:Q = [s, t, x, y, z]
我们一一扫描顶点, 然后找出相邻的顶点。计算每个相邻顶点之间的距离。
我们制作一个堆栈, 其中包含在计算出最短距离之后选择的那些顶点。
首先, 我们在堆栈M中取“”(这是来源)
M = [S] Q = [t, x, y, z]步骤2:现在找到t和y相邻的s。
Adj [s] → t, y [Here s is u and t and y are v]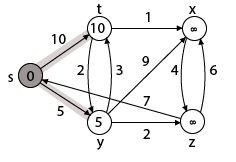
情况-(i)s→td [v]> d [u] + w [u, v] d [t]> d [s] + w [s, t]∞> 0 + 10 [假条件]然后d [t]←10π[t]←5调整[s]←t, y
情况-(ii)s→yd [v]> d [u] + w [u, v] d [y]> d [s] + w [s, y]∞> 0 + 5 [假条件]∞> 5然后d [y]←5π[y]←5
通过比较情况(i)和情况(ii)Adj [s]→t = 10, y = 5 y最短y被分配为5 = [s, y]
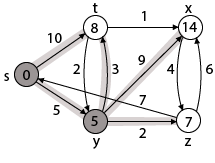
步骤3:现在找到y的相邻点, 即t, x, z。
Adj [y] → t, x, z [Here y is u and t, x, z are v]情况-(i)y→td [v]> d [u] + w [u, v] d [t]> d [y] + w [y, t] 10> 5 + 3 10> 8然后d [ t]←8π[t]←y
情况-(ii)y→xd [v]> d [u] + w [u, v] d [x]> d [y] + w [y, x]∞> 5 + 9∞> 14然后d [ x]←14π[x]←14
情况-(iii)y→zd [v]> d [u] + w [u, v] d [z]> d [y] + w [y, z]∞> 5 + 2∞> 7然后d [ z]←7π[z]←y
通过比较情况(i), 情况(ii)和情况(iii)Adj [y]→x = 14, t = 8, z = 7 z最短的z被分配为7 = [s, z]
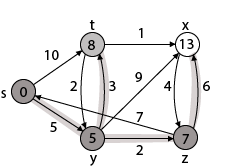
步骤-4现在, 我们将找到s, x的调整[z]
Adj [z] → [x, s] [Here z is u and s and x are v]情况-(i)z→xd [v]> d [u] + w [u, v] d [x]> d [z] + w [z, x] 14> 7 + 6 14> 13然后d [ x]←13π[x]←z
情况-(ii)z→sd [v]> d [u] + w [u, v] d [s]> d [z] + w [z, s] 0> 7 + 7 0> 14∴不满意, 因此将其丢弃。现在我们有x = 13。
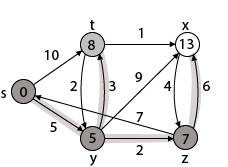
步骤5:现在我们将找到Adj [t]
调整[t]→[x, y] [这里t是u, x和y是v]
情况-(i)t→xd [v]> d [u] + w [u, v] d [x]> d [t] + w [t, x] 13> 8 + 1 13> 9然后d [ x]←9π[x]←t
情况-(ii)t→yd [v]> d [u] + w [u, v] d [y]> d [t] + w [t, y] 5> 10∴此条件不满足, 因此将被丢弃。
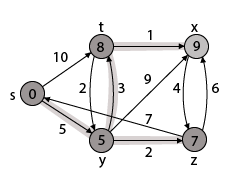
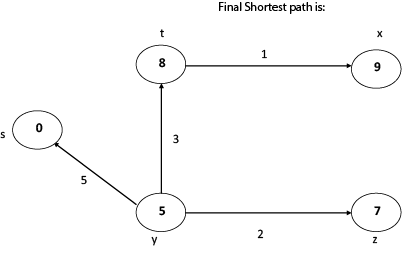
因此, 我们得到所有最短路径顶点为
从s到y的权重是5从s到z的权重是7从s到t的权重是8从s到x的权重
在给定的图中, 这是到光源的最短距离。
Dijkstra算法的缺点
- 它会进行盲目搜索, 因此在处理时会浪费大量时间。
- 它不能处理负边缘。
- 它导致无环图, 并且通常无法获得正确的最短路径。
- 我们需要跟踪已访问的顶点。




