回溯算法介绍

回溯是一种通过其他方式解决问题的算法方法。它使用递归方法来解释问题。可以说, 需要回溯才能找到所有可能的组合来解决优化问题。

回溯是一种尝试不同决策序列的系统方法, 直到找到一个可行的决策为止。

在下图中：

• 树中的每个非叶节点都是一个或多个其他节点（其子节点）的父节点
• 除了根之外, 树中的每个节点都只有一个父节点

但是, 通常, 我们将树木向下拖, 根部放在顶部。

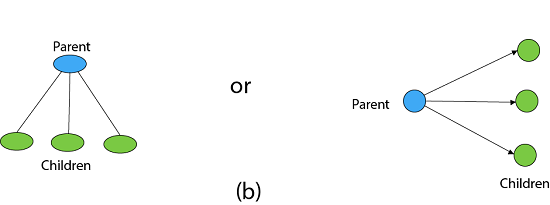
一棵树由节点组成。

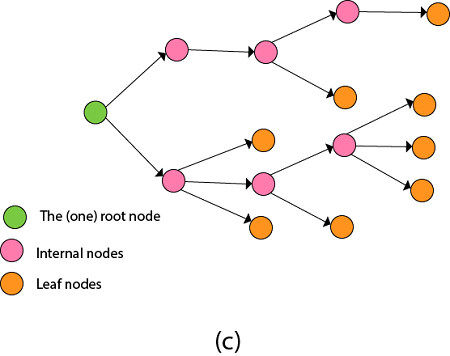
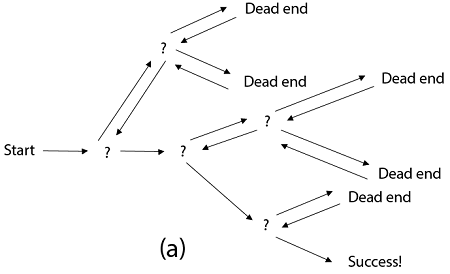
回溯可以理解为在树中搜索特定的“目标”叶节点。

回溯无疑非常简单-我们“探索”每个节点, 如下所示：

To "explore" node N:
 1. If N is a goal node, return "success"
 2. If N is a leaf node, return "failure"
 3. For each child C of N, Explore C
     If C was successful, return "success"
 4. Return "failure"

回溯算法通过系统地搜索给定问题的解空间来确定解。回溯是具有任何边界功能的深度优先搜索。需要使用回溯的所有解决方案来满足一组复杂的约束。约束可以是显式的或隐式的。

规定了显式约束, 它限制了要从给定集合中选择的每个向量元素。

隐式约束是规则, 它确定解空间中的每个元组实际上满足准则函数。