给定序列的子序列就是给定序列, 其中某些元素被省略。
给定两个序列X和Y, 如果Z是X和Y的子序列, 则我们说序列Z是X和Y的公共序列。
在最长的公共子序列问题中, 我们给定两个序列X =(x1 x2 …. xm)和Y =(y1 y2 yn), 并希望找到X和Y的最大长度公共子序列。LCS问题可以解决使用动态规划。
最长公共序列的特征
蛮力方法我们找到X的所有子序列, 并检查每个子序列是否也是Y的子序列, 这种方法需要指数时间, 因此对于长序列来说是不切实际的。
给定一个序列X =(x1 x2 ….. xm), 我们将i = 0、1和2 … m的X的第i个前缀定义为Xi =(x1 x2 ….. xi)。例如:如果X =(A, B, C, B, C, A, B, C), 则X4 =(A, B, C, B)
LCS的最佳子结构:令X =(x1 x2 …. xm)且Y =(y1 y2 …..)yn)为序列, 令Z =(z1 z2 … zk)是X和Y的任何LCS。
- 如果xm = yn, 则zk = x_m = yn, 并且Zk-1是Xm-1和Yn-1的LCS
- 如果xm≠yn, 则zk≠xm表示Z是Xm-1和Y的LCS。
- 如果xm≠yn, 则zk≠yn表示Z是X和Yn-1的LCS
步骤2:递归解决方案:LCS具有重叠的子问题属性, 因为要找到X和Y的LCS, 我们可能需要找到Xm-1和Yn-1的LCS。如果xm≠yn, 那么我们必须解决两个子问题, 找到X和Yn-1的LCS。只要这些LCS中较长的一个是x和y的LCS。但是, 这些子问题中的每一个都有找到Xm-1和Yn-1的LCS的子问题。
令c [i, j]为序列Xiand Yj的LCS的长度。如果i = 0和j = 0, 则其中一个序列的长度为0, 因此LCS的长度为0。LCS问题的最优子结构给定递归公式
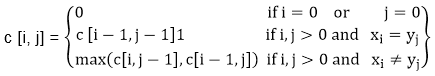
步骤3:计算LCS的长度:让两个序列X =(x1 x2 ….. xm)和Y =(y1 y2 ….. yn)作为输入。它将c [i, j]值存储在表c [0 … m, 0 ………. n]中。表b [1 ……… ..m, 1 ………. n]可以帮助我们构建最佳解决方案。 c [m, n]包含X, Y的LCS的长度。




