本文概述
二进制搜索树被组织在二进制树中。这样的树可以由链接的数据结构定义, 其中特定的节点是对象。除键字段外, 每个节点还包含字段left, right和p, 这些字段分别指向分别对应于其左子节点, 右子节点和父节点的节点。如果缺少孩子或父母, 则适当的字段包含值NIL。根节点是树中唯一其父字段为Nil的节点。
二进制搜索树属性
令x为二叉搜索树中的一个节点。
- 如果y是x左子树中的一个节点, 则键[y]≤键[k]。
- 如果z是x的右子树中的节点, 则键[x]≤键[y]。
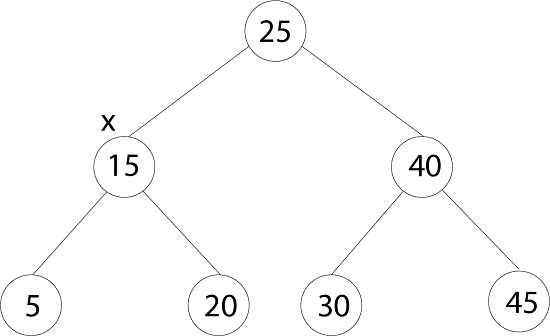
在此树中, 键[x] = 15
- 如果y是x左子树中的节点, 则键[y] = 5。
i.e. key [y] ≤ key[x].- 如果y是x的右子树中的节点, 则键[y] = 20。
i.e. key [x] ≤ key[y].二进制搜索树中的遍历
1. In-Order-Tree-Walk(x):始终按排序顺序在二进制搜索树中打印键。
INORDER-TREE-WALK (x) - Running time is θ(n)
1. If x ≠ NIL.
2. then INORDER-TREE-WALK (left [x])
3. print key [x]
4. INORDER-TREE-WALK (right [x])2. PREORDER-TREE-WALK(x):在其中我们访问根节点的先于任一子树中的节点。
PREORDER-TREE-WALK (x):
1. If x ≠ NIL.
2. then print key [x]
3. PREORDER-TREE-WALK (left [x]).
4. PREORDER-TREE-WALK (right [x]).3. POSTORDER-TREE-WALK(x):在其中我们访问根节点在其子树中的节点之后。
POSTORDER-TREE-WALK (x):
1. If x ≠ NIL.
2. then POSTORDER-TREE-WALK (left [x]).
3. POSTORDER-TREE-WALK (right [x]).
4. print key [x]查询二叉搜索树
1.搜索:TREE-SEARCH(x, k)算法在x的树节点中搜索键值等于k的节点。如果该节点不存在, 则返回指向该节点的指针。
TREE-SEARCH (x, k)
1. If x = NIL or k = key [x].
2. then return x.
3. If k < key [x].
4. then return TREE-SEARCH (left [x], k)
5. else return TREE-SEARCH (right [x], k)显然, 该算法在O(h)时间中运行, 其中h是树的高度。上述算法的迭代版本非常易于实现
ITERATIVE-TREE- SEARCH (x, k)
1. while x ≠ NIL and k ≠ key [k].
2. do if k < key [x].
3. then x ← left [x].
4. else x ← right [x].
5. return x.2.最小值和最大值:始终可以通过跟踪从根开始的左子指针直到遇到NIL来找到二进制搜索树中键为最小值的项。以下过程返回一个指针, 该指针指向以给定节点x为根的子树中的最小元素。
TREE- MINIMUM (x)
1. While left [x] ≠ NIL.
2. do x←left [x].
3. return x.TREE-MAXIMUM (x)
1. While left [x] ≠ NIL
2. do x←right [x].
3. return x.3.后继者和前任者:给定二叉树中的一个节点, 有时我们习惯按顺序树遍历确定的排序形式来查找其后继者。如果所有密钥都是特定的, 则节点x的后继节点是最小密钥大于key [x]的节点。二进制搜索树的结构使我们无需对键进行比较就可以统治节点的后继者。以下操作返回二进制搜索树中节点x的后继节点(如果存在), 如果x在树中具有最大关键字, 则返回NIL:
TREE SUCCESSOR (x)
1. If right [x] ≠ NIL.
2. Then return TREE-MINIMUM (right [x]))
3. y←p [x]
4. While y ≠ NIL and x = right [y]
5. do x←y
6. y←p[y]
7. return y.TREE-SUCCESSOR的代码分为两种情况。如果节点x的右子树是非空的, 则x的后继者只是右子树中的最左节点, 我们可以通过调用TREE-MINIMUM(右[x])在第2行中找到它。另一方面, 如果节点x的右子树为空, 并且x具有后继y, 则y是x的最低祖先, 其左子代也是x的祖先。为了找到y, 我们从x上快速上树, 直到遇到一个节点, 该节点是其父节点的左子节点。 TREE-SUCCESSOR的第3-7行处理这种情况。
TREE-SUCCESSOR在高度为h的树上的运行时间为O(h), 因为我们要么沿着树上的一条简单路径走, 要么沿着树下的一条简单路径走。与TREE-SUCCESSOR对称的过程TREE-PREDECESSOR也以时间O(h)运行。
4.在二进制搜索树中插入:要在二进制搜索树T中插入新值, 我们使用过程TREE-INSERT。该过程采用节点´, 其键[z] = v, 左[z] NIL, 右[z] = NIL。它以插入树中适当位置的方式修改T和z的某些属性。
TREE-INSERT (T, z)
1. y ←NIL.
2. x←root [T]
3. while x ≠ NIL.
4. do y←x
5. if key [z]< key [x]
6. then x←left [x].
7. else x←right [x].
8. p [z]←y
9. if y = NIL.
10. then root [T]←z
11. else if key [z] < key [y]
12. then left [y]←z例如:
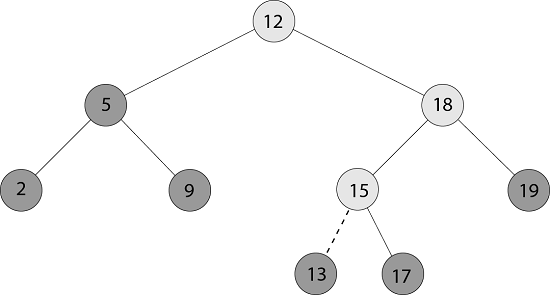
图:TREE-INSERT的工作
假设我们想将一个键为13的项目插入二叉搜索树。
x = 1
y = 1 as x ≠ NIL.
Key [z] < key [x]
13 < not equal to 12.
x ←right [x].
x ←3
Again x ≠ NIL
y ←3
key [z] < key [x]
13 < 18
x←left [x]
x←6
Again x ≠ NIL, y←6
13 < 15
x←left [x]
x←NIL
p [z]←6现在, 我们的节点z将是其父节点(y)的左或右子节点。
key [z] < key [y]
13 < 15
Left [y] ← z
Left [6] ← z因此, 在节点索引左侧的6处插入一个节点。
5.二进制搜索树中的删除:从树中删除节点时, 必须维护树中隐式的任何关系。将考虑从二叉搜索树中删除节点:
有三种不同的情况:
- 没有子节点:这种情况很简单。只需将父节点指向待删除节点的指针设置为nil, 然后删除该节点即可。
- 具有一个子节点的节点:当z没有左子节点时, 我们将z替换为其右子节点, 该子节点可能为NIL, 也可能不是NIL。当z没有合适的子代时, 我们将z替换为其合适的子代。
- 具有两个子节点的节点:当z同时具有左子节点和右子节点时。我们发现z的后继者y, 它位于右z的右子树中, 并且没有左子节点(z的后继者将是一个带有其右子树的最小值的节点, 因此它没有左子节点)。如果y是z的正确子代, 则替换z。否则, y位于z的右子树内, 而不位于z的右子树内。在这种情况下, 我们首先将z替换为其自己的右孩子, 并将z替换为y。
TREE-DELETE (T, z)
1. If left [z] = NIL or right [z] = NIL.
2. Then y ← z
3. Else y ← TREE- SUCCESSOR (z)
4. If left [y] ≠ NIL.
5. Then x ← left [y]
6. Else x ← right [y]
7. If x ≠NIL
8. Then p[x] ← p [y]
9. If p[y] = NIL.
10. Then root [T] ← x
11. Else if y = left [p[y]]
12. Then left [p[y]] ← x
13. Else right [p[y]] ← y
14. If y ≠ z.
15. Then key [z] ← key [y]
16. If y has other fields, copy them, too.
17. Return y该过程以O(h)时间在高度为h的树上运行。
例如:从二叉搜索树中删除节点z。节点z可以是根, 节点q的左子节点或q的右子节点。
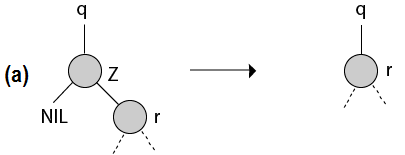
Z是唯一的合适孩子。
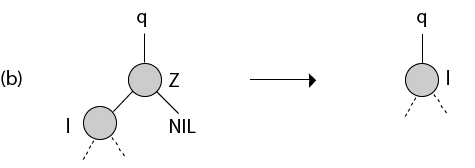
Z是唯一的左孩子。我们用l代替z。
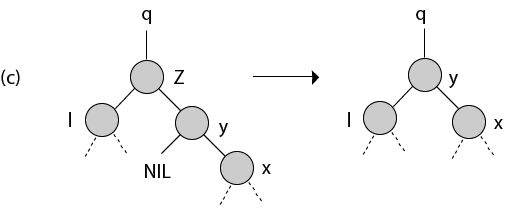
节点z有两个孩子;它的左子节点是节点l, 右子节点是后继节点y, y的右子节点是节点x。我们用y替换z, 将y的左孩子更新为l, 但是将x保留为y的右边孩子。
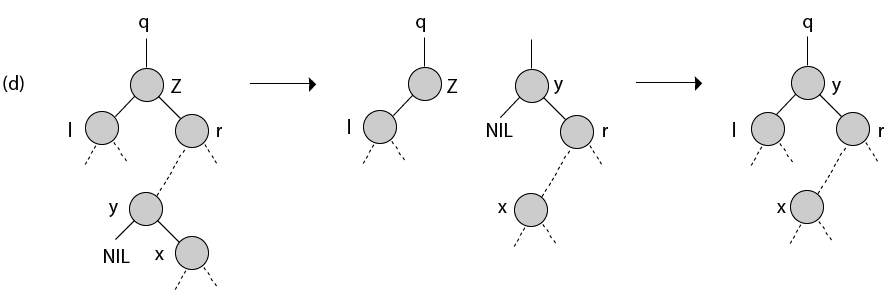
节点z有两个子节点(左子节点l和右子节点r), 其后继节点y≠r位于以r为根的子树中。我们用自己的右子x替换y, 并将y设为r的父代。然后, 我们将y设置为q的孩子和l的父母。




