散列方法实现详解

本文概述

• 1.链式散列
• 2.使用开放式地址进行哈希处理

有两种用于实现哈希的主要方法：

1. 链式散列
2. 使用开放式地址进行哈希处理

1.链式散列

在“通过链式哈希处理”中, S中的元素存储在大小为m的哈希表T [0 … m-1]中, 其中m大于S的大小n。哈希表被称为具有m个插槽。与散列方案相关联的是从U映射到{0 … m-1}的散列函数h。每个密钥k∈S存储在位置T [h（k）]中, 我们说k被散列了插入插槽h（k）。如果将S中的多个键散列到同一插槽中, 则发生冲突。

在这种情况下, 将散列到同一插槽中的所有密钥放置在与该插槽关联的链接列表中, 该链接列表称为插槽中的链。哈希表的负载因子定义为∝ = n / m, 它表示每个插槽的平均密钥数。我们通常在m =θ（n）的范围内操作, 因此usually通常为常数, 通常∝ <1。

链式碰撞解决方案：

在链接中, 我们将哈希到同一插槽的所有元素放入同一链表, 如图所示, 插槽j包含一个指针, 该指针指向哈希到j的所有存储元素的列表的开头；如果没有这样的元素, 则插槽j包含NIL。

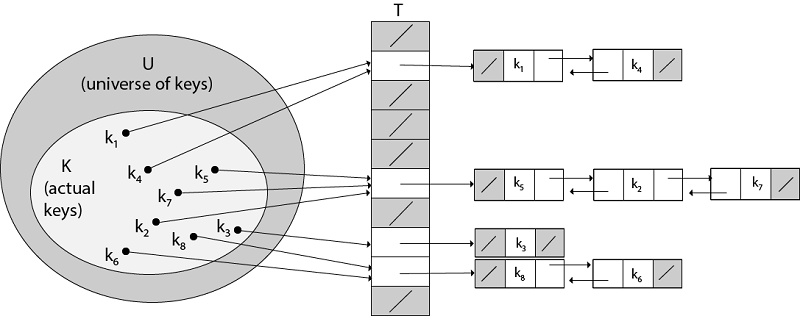
图：通过链接解决冲突。

每个哈希表槽T [j]包含哈希值为j的所有键的链表。

例如, h（k1）= h（k4）和h（k5）= h（k7）= h（K2）。链表可以是单链也可以是双链。我们将其显示为双向链接, 因为这样删除速度更快。

链式散列分析：

给定具有存储n个元素的m个插槽的哈希表T, 我们将T的负载因子α定义为n / m, 即链中存储的元素的平均数量。因此, 最坏情况下的搜索运行时间为θ（n）加上计算哈希函数的时间, 这比我们对所有元素使用一个链表的情况更好。显然, 哈希表并不用于最坏的情况。

平均而言, 散列的平均性能取决于散列函数h在m个插槽之间分配要存储的密钥集的程度。

示例：让我们考虑将元素5、28、19、15、20、33、12、17、10插入链式哈希表中。让我们假设哈希表有9个时隙, 哈希函数为h（k）= k mod 9。

解决方案：链式哈希表的初始状态

插入5：

h (5) = 5 mod 9 =5

为T [5]创建一个链表, 并在其中存储值5。

同样, 插入28。h（28）= 28 mod 9 = 1。为T [1]创建一个链接列表, 并在其中存储值28。现在插入19 h（19）= 19 mod 9 =1。将值19插入到链表的开头的插槽T [1]中。

Now insert h 15, h (15) = 15 mod 9 = 6. Create a link list for T [6] and store value 15 in it.
Similarly, insert 20, h (20) = 20 mod 9 = 2 in T [2].
Insert 33, h (33) = 33 mod 9 = 6
In the beginning of the linked list T [6]. Then, Insert 12, h (12) = 12 mod 9 = 3 in T [3].
    Insert 17, h (17) = 17 mod 9 = 8 in T [8].
    Insert 10, h (10) = 10 mod 9 = 1 in T [1].

因此, 插入键10之后的链式哈希表为

2.使用开放式地址进行哈希处理

在开放式寻址中, 所有元素都存储在哈希表本身中。也就是说, 每个表条目都由动态集或NIL的组成部分组成。搜索项目时, 我们会一直检查表槽, 直到找到所需的对象或确定该元素不在表中为止。因此, 在开放式寻址中, 负载系数α决不能超过1。

开放式寻址的优点是避免了指针。在此, 我们计算要检查的时隙序列。通过不共享指针释放的额外内存为哈希表提供了相同数量内存的大量插槽, 从而可能减少冲突并加快检索速度。

检查哈希表中位置的过程称为探测。

因此, 哈希函数变为

h : U x {0, 1, ....m-1}  →  {0, 1, ...., m-1}.

对于开放式寻址, 我们要求对于每个密钥k, 探测序列

{h, (k, 0), h (k, 1)....h (k, m-1)}
Be a Permutation of (0, 1...... m-1)

HASH-INSERT过程将哈希表T和密钥k作为输入

HASH-INSERT (T, k)
 1. i ← 0
 2. repeat j ← h (k, i)
 3. if T [j] = NIL
 4. then T [j] ← k
 5. return j
 6. else ← i= i +1
 7. until i=m
 8. error "hash table overflow"

HASH-SEARCH过程将哈希表T和密钥k作为输入, 如果发现时隙j包含密钥k, 则返回j；如果表T中不存在密钥k, 则返回NIL。

HASH-SEARCH.T (k)
 1. i ← 0
 2. repeat j ← h (k, i)
 3. if T [j] =j
 4. then return j
 5. i ← i+1
 6. until T [j] = NIL or i=m
 7. return NIL

---