本文概述
这是一种线性时间排序算法, 通过不进行比较, 可以更快地工作。假设要排序的数字在1到k的范围内, 其中k很小。
基本思想是确定最终排序数组中每个数字的“等级”。
计数排序使用三个数组
- [1, n]保留初始输入。
- B [1, n]保存排序的输出。
- C [1, k]是整数数组。 C [x]是x在A中的等级, 其中x∈[1, k]
首先, C [x]是A [j]的元素数量, 它们等于x
- 将C初始化为零
- 对于从1到n的每个j, 将C [A [j]]递增1
我们设置B [C [x]] = A [j]
如果有重复项, 我们将在复制后递减C [i]。
Counting Sort (array P, array Q, int k)
1. For i ← 1 to k
2. do C [i] ← 0 [ θ(k) times]
3. for j ← 1 to length [A]
4. do C[A[j]] ← C [A [j]]+1 [θ(n) times]
5. // C [i] now contain the number of elements equal to i
6. for i ← 2 to k
7. do C [i] ← C [i] + C[i-1] [θ(k) times]
8. //C[i] now contain the number of elements ≤ i
9. for j ← length [A] down to 1 [θ(n) times]
10. do B[C[A[j] ← A [j]
11. C[A[j] ← C[A[j]-1说明:
步骤1:for循环将数组R初始化为“ o”。但是在第一步中, 将循环变量1初始化为k或将0初始化为k存在矛盾。由于0-1是基于最小值的, 因此出现在数组A(输入数组)中。基本上, 我们从输入数组’A’中的最小值开始
对于步骤3到4的循环, 检查每个输入元素。如果输入元素的值为“ i”, 则将C [i]递增。因此, 在步骤5之后, 对于每个整数i = 0、1、2 ….. k, C [i]保持输入元素的数量等于I。
循环的步骤6至8确定每个i = 0、1 …..多少个输入元素小于或等于i
对于步骤9到11的循环, 将每个元素A [j]放入输出数组B中的正确排序位置。对于每个A [j], 值C [A [j]]是A [j]的正确最终位置输出数组B中的[], 因为有C [A [j]]个元素小于或等于A [i]。
因为元素可能并不唯一, 所以每次将值A [j]放入数组B时, 我们就将C [A [j]减1。 , 移到输出数组中A [j]之前的位置。
运行时间分析
- 对于第1步到第2步的循环, 取θ(k)倍
- 对于第3步到第4步的循环, 取θ(n)倍
- 对于步骤6至7的循环, 取θ(k)倍
- 对于步骤9至11的循环, 取θ(n)倍
总时间是θ(k + n)时间。
注意:
- 计数排序具有一个稳定的重要属性:具有相同值的数字在输出数组中的出现顺序与在输入数组中的出现顺序相同。
- “计数排序”在“基数排序”中用作子例程。
示例:举例说明数组中计数排序的操作。
A= ( 7, 1, 3, 1, 2, 4, 5, 7, 2, 4, 3)解:

图:初始A和C阵列
For j=1 to 11
J=1, C [1, k] =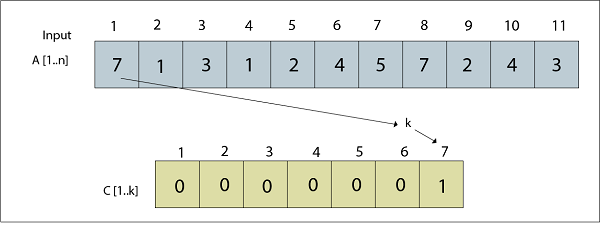
图:A [1] = 7已处理
J=2, C [1, k] =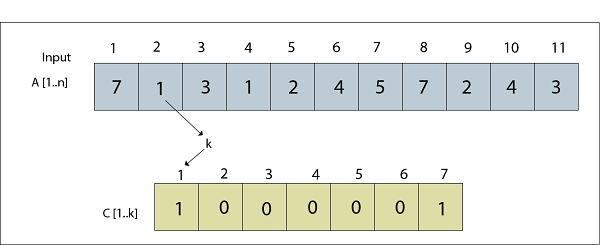
图:A [2] = 1已处理
J=3, C [1, k]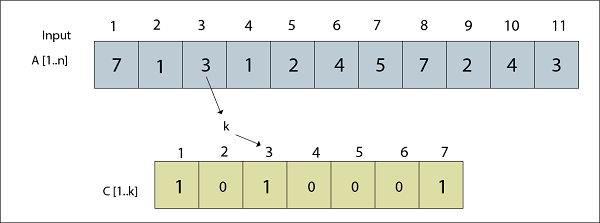
图:A [3] = 3已处理
J=4, C [1, k]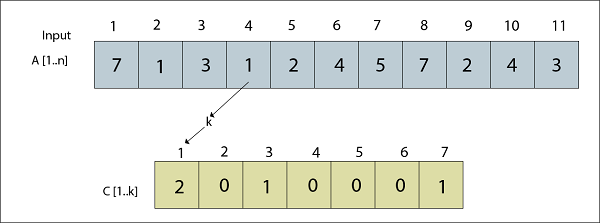
图:A [4] = 1已处理
J=5, C [1, k]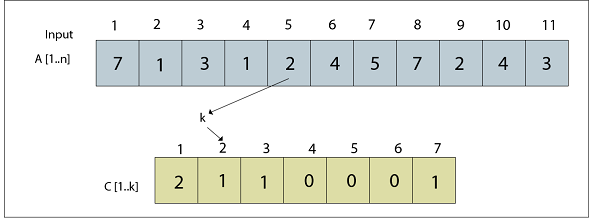
图:A [5] = 2已处理
更新后的C为:

图:C现在包含A元素的数量
注意:这里将逐个扫描“ A”项并将其置于“ C”中的位置, 并且将在“ C”数组中的项中提及访问该项目的次数, 并且将其更新或计数器增加如果再次访问任何项目, 则为1。
现在, 将使用以下语句执行for循环i = 2至7:
C [i] = C [i] + C [i-1]通过应用这些条件, 我们将按照我所说的将C更新为2到7
C [2] = C [2] + C [1] C [3] = C [3] + C [2]
C [2] = 2 + 2 C [3] = 2 + 4
C [2] = 4 C [3] = 6
C [4] = C [4] + C [3] C [5] = C [5] + C [4]
C [4] = 2 + 6 C [5] = 1 +8
C [4] = 8 C [5] = 9
C [6] = C [6] + C [5] C [7] = C [7] + C [6]
C [6] = 0 + 9 C [7] = 2 + 9
C [6] = 9 C [7] = 11因此, 更新后的C为:

图:C设置为对A的每个数字进行排名
现在, 我们将找到新的数组B
现在有两个条件适用:
- B [C [A [j]←A [j]
- C [A [j]←C [A [j] -1
我们将计数器一减一, 然后从最后一个位置开始扫描A中的元素。 A中的元素成为C中的职位
For j ← 11 to 1步骤1
B [C [A [11]]] = A [11] C [A [11] = C [A [11]-1
B [C [3] = 3 C [3] = C [3] -1
B [6] = 3 C [3] = 5
图:A [11]放置在输出数组B中
第2步
B [C [A [10]]] = A [10] C [A [10]] = C [A [10]]-1
B [C [4]] =4 C [4] = C [4] -1
B [8] = 4 C [4] = 7
图:A [10]放置在输出数组B中
第三步
B [C [A [9]] = A [9] C [A [9] = C [A [9]]-1
B [C [2]] = A [2] C [2] = C [2]-1
B [4] = 2 C [2] = 3
图:A [9]放置在输出数组B中
步骤4
B [C [A [8]]] = A [8] C [A [8]] =C [A [8]] -1
B [C [7]] =7 C [A [8]] = C [7]-1
B [11] =7 C [7] = 10
图:A [8]放置在输出数组B中
第5步
B [C [A [7]]] = A [7] C [A [7]] = C [A [7]] - 1
B [C [5]] = 5 C [5] = C [5] - 1
B [9] = 5 C [5] =8
图:A [7]放置在输出数组B中
第6步
B [C [A [6]]] = A [6] C [A [6]] = C [A [6]] - 1
B [C [4]] = 4 C [4] = C [4] - 1
B [7] = 4 C [4] = 6
图:A [6]放置在输出数组B中
步骤7
B [C [A [5]]] = A [5] C [A [5] = C [A [5]] -1
B [C [2] =2 C [2] = C [2] - 1
B [3] = 2 C [2] = 2
图:A [5]放置在输出数组B中
步骤8
B [C [A [4]]] = A [4] C [A [4]] = C [A [4]] - 1
B [C [1] = 1 C [1] = C [1] - 1
B [2] = 1 C [1] = 1
图:A [4]放置在输出数组B中
步骤9
B [C [A [3]]] = A [3] C [A [3]] = C [A [3]] - 1
B [C [3] = 3 C [3] = C [3] - 1
B [5] = 3 C [3] = 4
图:A [3]放置在输出数组B中
第10步
B [C [A [2]]] = A [2] C [A [2]] = C [A [2]] - 1
B [C [1]] = 1 C [1] = C [1] - 1
B [1] = 1 C [1] = 0
图:A [2]放置在输出数组B中
步骤11
B [C [A [1]]] = A [1] C [A [1]] = C [A [1]] - 1
B [C [7]] = 7 C [7] = C [7] - 1
B [10] = 7 C [7] = 9
图:B现在包含最终排序的数据。




