下界理论概念基于执行算法所需的最短时间的计算, 被称为下界理论或基础界理论。
下界理论使用多种方法/技术来找出下界。
概念/目标:主要目标是计算执行算法所需的最小比较数。
技术技巧
下界理论使用的技术是:
- 比较树。
- 甲骨文和对手的争论
- 状态空间法
1.比较树:
在比较排序中, 我们仅使用元素之间的比较来获取有关输入序列(a1; a2 … an)的顺序信息。
给定(a1, a2 ….. an)中的ai, aj我们执行比较之一
- ai <aj小于
- ai≤aj小于或等于
- ai> aj大于
- ai≥aj大于或等于
- ai = aj等于
要确定它们的相对顺序, 如果我们假设所有元素都是不同的, 那么我们只需要考虑ai≤aj’=’被排除且&, ≥, ≤, >, <等价。
考虑对三个数字a1, a2和a3进行排序。有3个! = 6种可能的组合:
(a1, a2, a3), (a1, a3, a2), (a2, a1, a3), (a2, a3, a1)
(a3, a1, a2), (a3, a2, a1)基于比较的算法定义了决策树。
决策树:决策树是一个完整的二叉树, 显示了元素之间的比较, 这些元素由在给定大小的输入上运行的适当排序算法执行。控制, 数据移动和该算法的所有其他条件都将被忽略。
在决策树中, 将存在一个长度为n的数组。
因此, 总叶子数为n! (即比较总数)
如果树高是h, 那么肯定
n! ≤2n (tree will be binary)以比较a1, a2和a3的示例为例。
左子树将是真实条件, 即ai≤aj
正确的子树将是错误条件, 即ai> aj
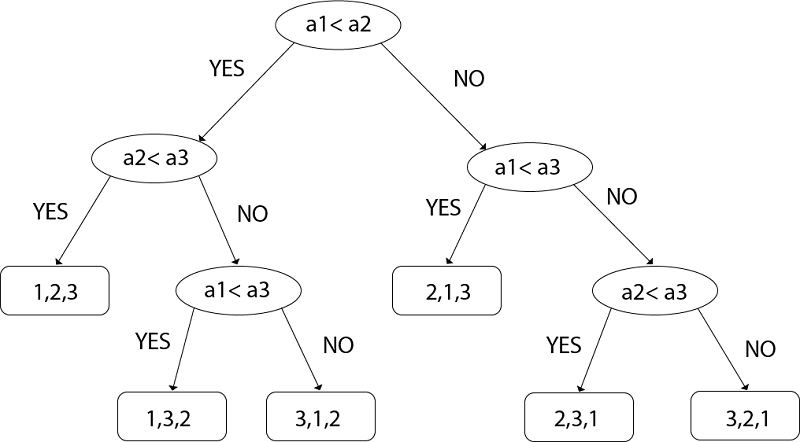
图:决策树
所以从上面, 我们得到了
N! ≤2n两边取原木

二进制搜索的比较树:
示例:假设我们有一个根据以下位置的项目清单:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14
最后一个中点是:
2, 4, 6, 8, 10, 12, 14因此, 我们将考虑所有中点, 并通过逐步设置中点来制作一棵树。
粗体字母是此处的中点
根据Mid-Point, 这棵树将是:
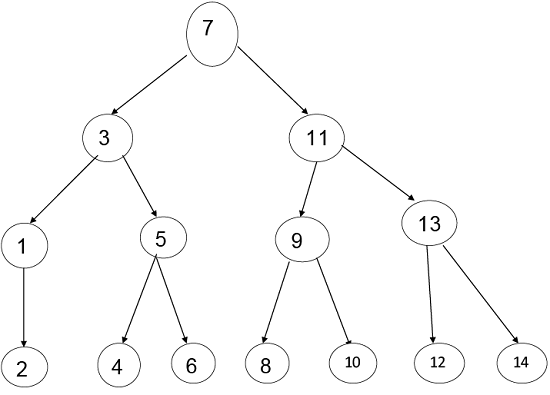
步骤1:内部节点的k级以内的最大节点数为2k-1
例如
2k-1
23-1= 8-1=7
Where k = level=3步骤2:比较树中内部节点的最大数量为n!
注意:这里内部节点是叶子。
步骤3:从Condition1和Condition 2中, 我们得到
N! ≤ 2k-1
14 < 15
Where N = Nodes第4步:现在, n + 1≤2k
在此, 二进制搜索中的内部节点将始终小于2k。
第五步:
n+1<= 2k
Log (n+1) = k log 2
k >=
k >=log2(n+1)第六步:
T (n) = k步骤7:
T (n) >=log2(n+1)此处, 使用Binary Search执行n个词项搜索任务的最小比较数
2. Oracle和对手的争论:
获得下限的另一种技术包括使用“ oracle”。
给定某种估计模型(例如比较树), oracle将告诉我们每个比较的结果。
为了得出一个好的下限, oracle尽力使该算法尽可能地努力工作。
它通过确定下一个分析的结果来进行此操作, 该结果对确定最终答案最重要。
并且通过保持已完成工作的步骤, 可以得出问题的最坏情况下限。
示例:(合并问题)给定集合A(1:m)和B(1:n), 其中对A和B中的信息进行了排序。考虑组合这两个集合以给出单个排序集合的算法的下界。
考虑所有m + n个元素都是特定的, 并且A(1)<A(2)<…. <A(m)和B(1)<B(2)<…. <B(n )。
基本组合告诉我们, A和B可以通过C((m + n), n))种方式合并在一起, 同时仍保留A和B内的顺序。
因此, 如果我们需要比较树作为用于组合算法的模型, 那么将存在C((m + n), n)个外部节点, 因此至少需要log C((m + n), m)个比较。任何基于比较的合并算法。
如果我们让MERGE(m, n)为用于合并m个项目和n个项目的最小比较数, 则我们有不等式
Log C ((m+n), m) MERGE (m, n) m+n-1.当m远小于n时, 上限和下限会迅速分开。
3.状态空间法:
1.状态空间方法是一组规则, 这些规则显示算法可以从单个比较的给定状态中假设的可能状态(n个元组)。
2.一旦给出状态转换, 就可以通过争辩说使用更少的转换就无法达到最终状态, 从而得出下界。
3.给定n个不同的项目, 找到赢家和输家。
4.目的:当状态改变时, 计数是状态空间法的目标。
5.在这种方法中, 我们将通过计算状态变化次数来计算比较次数。
6.通过状态空间法分析问题, 找出最小和最大的项目。
7.状态:它是属性的集合。
8.通过这种方式, 我们可以解决两种类型的问题:
- 从元素数组中找到最大和最小的元素。
- 从元素数组中找出最大和第二大元素。
9.对于最大的项目, 我们需要进行7次比较, 第二大的项目将是什么?
Now we count those teams who lose the match with team A
Teams are: B, D, and E
So the total no of comparisons are: 7
Let n is the total number of items, then
Comparisons = n-1 (to find the biggest item)
No of Comparisons to find out the 2nd biggest item = log2n-110.在这种情况下, 没有一个比较等于算法执行过程中状态的改变次数。
示例:州(A, B, C, D)
- 没有无法比拟的项目。
- 没有赢但从未丢失的项目(最终赢家)。
- 没有丢失但从未赢过的物品(最终失败者)
- 没有那些有时会输赢的项目。
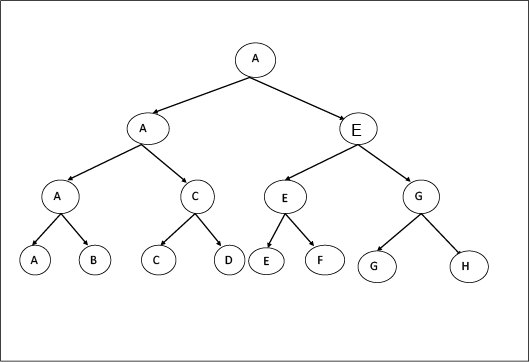
首先, A, B比较或匹配它们。 A赢, C赢, DC赢, 依此类推。我们可以假设B获胜, 依此类推。我们可以假设B代替A获胜, 这取决于我们自己。

在阶段1中, 有4个状态, 如果团队为8个, 则有4个状态, 就像n个团队为n / 2个状态一样。
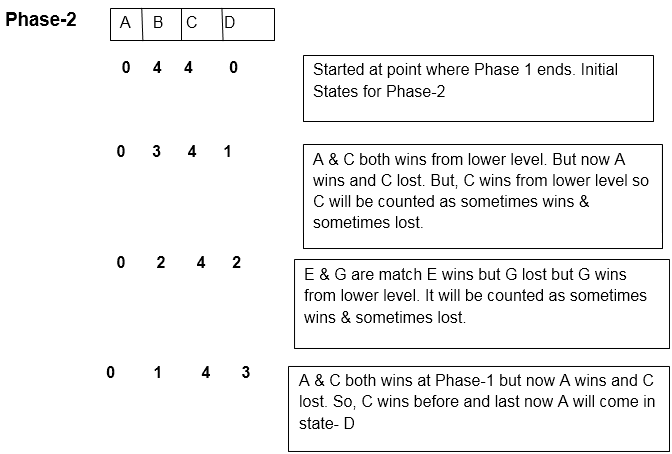
4在C状态下是不变的, 因为B, D, F, H是永远不会赢的失利球队。
因此, 在阶段2中有3个状态, 如果n为8, 则状态为3, 如果n个团队为状态。
阶段3:在此阶段中, 将考虑处于C州之下的球队, 并且他们之间将进行比赛以找出根本无法获胜的球队。
在此结构中, 我们将向上移动以表示比赛后谁没有获胜。
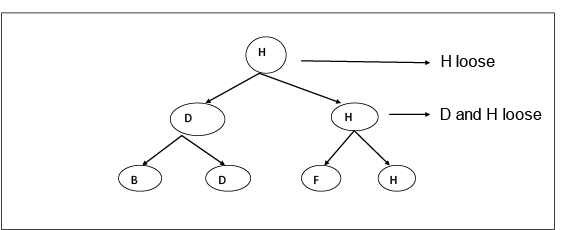
在这里, H是一支从未赢过的球队。这样, 我们实现了我们的第二个目标。

因此, 在阶段-3中有3个州
注意:所有状态的总和始终等于’n’。
因此, 通过添加所有相的状态, 我们将得到:
阶段1 +阶段2 +阶段3
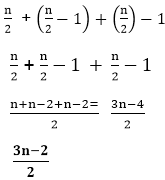
假设我们有8支球队, 然后有状态(至少)来找出哪支球队永远不会赢。
因此, 公式为:
下界(L(n))是特定问题的属性, 即排序问题, 矩阵乘法而不是解决该问题的任何特定算法。
下界理论说, 任何计算都不能以小于任意输入的单位(L(n))倍的活动来进行活动, 即在最坏的情况下, 每个基于比较的排序算法必须至少花费L(n)时间。
L(n)是最可能完成的基本总体可能的计算。
利用较小的下限来产生约束, 最好的替代方法是计算问题输入中必须准备的元素数量和需要产生的输出项目的数量。
下限理论是一种已被用来以可能的最有效方式建立给定算法的方法。这是通过发现一个函数g(n)来完成的, 该函数在任何算法解决给定问题所需的时间上都有一个下限。现在, 如果我们有一个算法, 其计算时间与g(n)相同, 那么我们知道渐近地我们不能做得更好。
如果f(n)是某种算法的时间, 那么我们写f(n)=Ω(g(n))表示g(n)是f(n)的下限。如果存在正常数c和n0使得| f(n)|成立, 则该方程式可以正式写成。 > = c | g(n)|对于所有n> n0。除了在恒定因子内开发下限外, 我们更加意识到在可能的情况下确定更精确范围的事实。
推导好的下限比安排有效的算法更具挑战性。发生这种情况是因为下限说明了有关解决问题的所有可能算法的事实。通常, 我们无法枚举和分析所有这些算法, 因此通常很难获得下界证明。




