汉诺塔问题

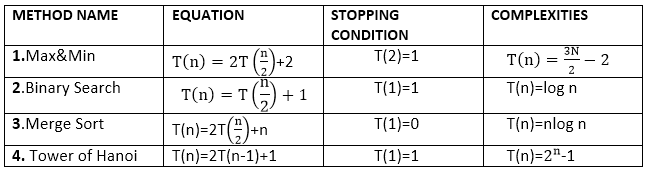
1.这是一个经典问题, 你尝试仅使用三个销将所有磁盘从一个销移动到另一个销。

2.最初, 所有磁盘都堆叠在一起, 较大的磁盘位于较小的磁盘下面。

3.尝试重新放置所有磁盘时, 可以将磁盘移动到三个销钉中的任何一个, 但是不能将较大的磁盘放在较小的磁盘上, 并且一次只能转移一个磁盘。

通过分而治之算法可以轻松解决此问题

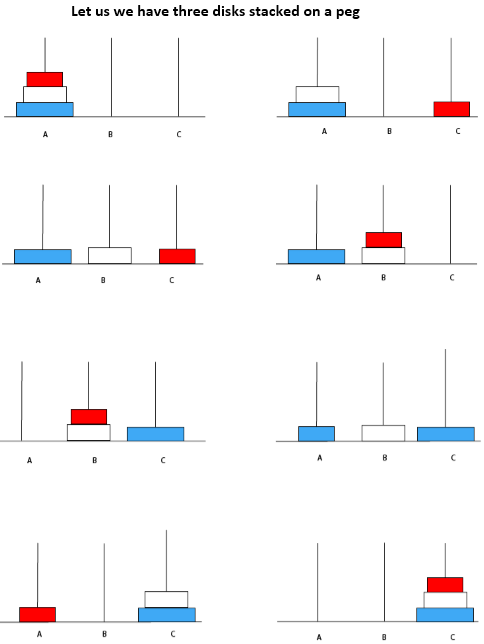
在上面的第7步中, 将钉A的所有磁盘都转移到C, 并满足以下条件：

1. 一次只能移动一个磁盘。
2. 较小的磁盘可以放在较大的磁盘上。

令T（n）为将n个磁盘从钉A移到钉C所需的总时间

1. 将n-1个磁盘从第一个钉移到第二个钉。这可以在T（n-1）个步骤中完成。
2. 将较大的磁盘从第一钉移到第三钉将需要第一步。
3. 将n-1个磁盘从第二个桩递归移动到第三个桩将再次需要T（n-1）步骤。

因此, 总耗时T（n）= T（n-1）+1+ T（n-1）

汉诺塔问题的关系公式为：

我们得到

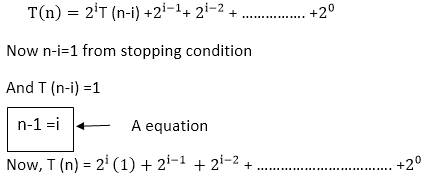
它是具有公共比率的几何级数级数, r = 2第一项, a = 1（20）

当我们必须将n个磁盘从一个钉移到另一个时, B方程是汉诺塔问题技术所需的复杂性。

T（3）= 23-1 = 8-1 = 7年

[在概念上, 我们已经证明了将由通用方程式证明的7个步骤]

汉诺塔问题计划：

#include<stdio.h>
void towers(int, char, char, char);
 int main()
 {
       int num;
       printf ("Enter the number of disks : ");
        scanf ("%d", &num);
      printf ("The sequence of moves involved in the Tower of Hanoi are :\n");
      towers (num, 'A', 'C', 'B');
      return 0;
 
}
     void towers( int num, char from peg, char topeg, char auxpeg)
 {
           if (num == 1)
 {
       printf ("\n Move disk 1 from peg %c to peg %c", from peg, topeg);
           return;
 }
   Towers (num - 1, from peg, auxpeg, topeg);
    Printf ("\n Move disk %d from peg %c to peg %c", num, from peg, topeg);
   Towers (num - 1, auxpeg, topeg, from peg);
 }

输出：

Enter the number of disks: 3
The sequence of moves involved in the Tower of Hanoi is
Move disk 1 from peg A to peg C
Move disk 2 from peg A to peg B
Move disk 1 from peg C to peg B
Move disk 3 from peg A to peg C
Move disk 1 from peg B to peg A
Move disk 2 from peg B to peg C
Move disk 1 from peg A to peg