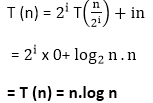合并排序算法

它紧密遵循分而治之范式。

从概念上讲, 它的工作方式如下：

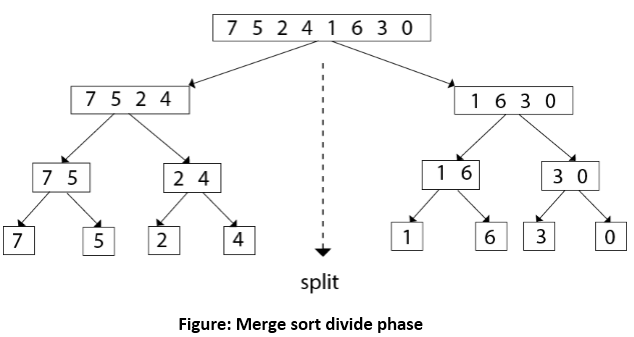
1. 划分：将未排序的列表划分为两个大小约为一半的子列表。
2. 征服：递归地对两个子列表中的每个列表进行排序, 直到列表大小为1, 在这种情况下, 将返回列表项。
3. 合并：将两个已排序的“子”列表重新合并为一个已排序的列表。

主要目的是按降序对未排序列表进行排序。

ALGORITHM-MERGE SORT
1. If p<r
2. Then q ← ( p+ r)/2
3. MERGE-SORT (A, p, q)
4. MERGE-SORT ( A, q+1, r)
5. MERGE ( A, p, q , r)

下图说明了分割（分割）过程。

FUNCTIONS: MERGE (A, p, q, r)
1. n 1 = q-p+1
2. n 2= r-q
3. create arrays [1.....n 1 + 1] and R [ 1.....n 2 +1 ]
4. for i ← 1 to n 1
5. do [i] ← A [ p+ i-1]
6. for j ← 1 to n2
7. do R[j] ← A[ q + j]
8. L [n 1+ 1] ← ∞
9. R[n 2+ 1] ← ∞ 
10. I ← 1
11. J ← 1
12. For k ← p to r
13. Do if L [i] ≤ R[j]
14. then A[k] ← L[ i]
15. i ← i +1
16. else A[k] ← R[j]
17. j ← j+1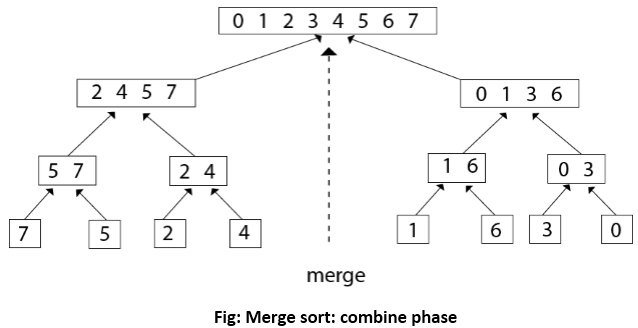

在这种方法中, 我们将给定的列表分为两半。然后递归分析合并排序和划分。我们得到许多排序列表。

最后, 我们结合了排序列表。

合并排序分析

令T（n）为合并排序中花费的总时间

1. 在最多2T的时间将两半分选
2. 当我们合并排序列表时, 我们总共有n-1个比较, 因为只需要将要保留的最后一个元素复制到合并列表中, 就不会进行比较。

因此, 关系公式变为

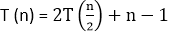
但是我们忽略了“ -1”, 因为该元素将需要一些时间才能复制到合并列表中。

所以T（n）= 2T + n ……等式1

注意：停止条件T（1）= 0, 因为最后只剩下1个元素需要复制, 并且将不进行比较。

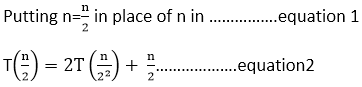
将2个等式放在1个等式中

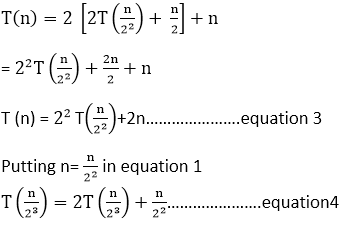
将4个等式放在3个等式中

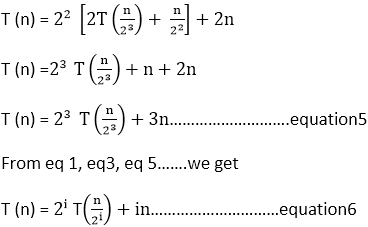
从停止条件开始：

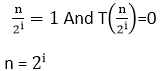
双面应用日志：

log n = log2i logn = i log2 = i log2n = i

从6等式

---