分治算法简介

分而治之是一种算法模式。在算法方法中, 设计是对巨大输入进行争议, 将输入分成小块, 在每个小块上确定问题, 然后将分段解决方案合并为全局解决方案。解决问题的这种机制称为分而治之策略。

分而治之算法由使用以下三个步骤的争议组成。

1. 将原始问题分为一组子问题。
2. 征服：递归地分别解决每个子问题。
3. 合并：将子问题的解决方案放在一起, 以得到整个问题的解决方案。

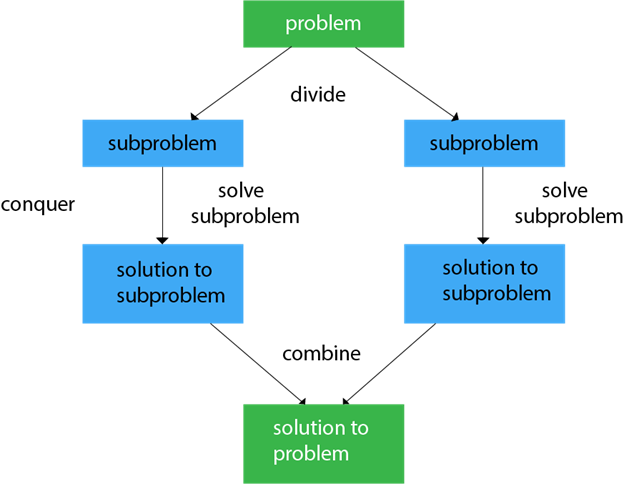
通常, 我们可以在三步过程中遵循分而治之的方法。

示例：具体的计算机算法基于分而治之方法：

1. 最大和最小问题
2. 二元搜寻
3. 排序（合并排序, 快速排序）
4. 河内塔。

分而治之基础

分而治之策略有两个基本原则：

1. 关系公式
2. 停止条件

1.关系公式：这是我们从给定技术中生成的公式。在生成公式之后, 我们将应用D＆C策略, 即, 我们递归解决问题并解决破碎的子问题。

2.停止条件：当我们使用分而治之策略解决问题时, 我们需要知道需要花多少时间应用分而治之。因此, 需要停止D＆C递归步骤的条件称为“停止条件”。