分析算法控制结构

本文概述

• for循环的复杂性
• 算法

要分析编程代码或算法, 我们必须注意到每条指令都会影响算法的整体性能, 因此, 必须单独分析每条指令以分析整体性能。但是, 每个编程代码中都有一些算法控制结构, 它们具有特定的渐近分析。

一些算法控制结构是：

1. 排序
2. 如果-然后-其他
3. for循环
4. While循环

---

1.排序：

假设我们的算法由A和B两部分组成。A花费时间tA, B花费时间tB进​​行计算。总计算“ tA + tB”是根据顺序规则进行的。根据最大规则, 此计算时间为（max（tA, tB））。

例：

Suppose tA =O (n) and tB = θ (n2). 
Then, the  total computation time can be calculated as

Computation Time = tA + tB
 = (max (tA, tB)
 = (max (O (n), θ (n2)) = θ (n2)

2.如果-然后-其他：

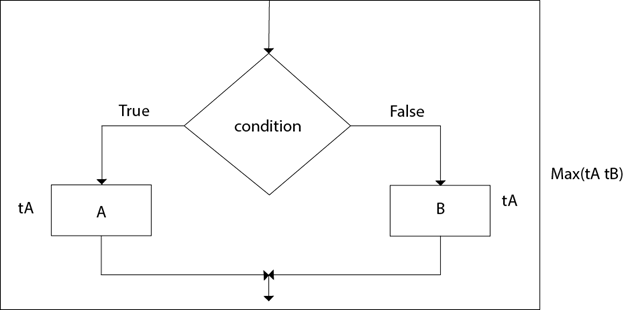
总时间的计算是根据条件规则“ if-then-else”进行的。根据最大规则, 此计算时间为max（tA, tB）。

例：

Suppose tA = O (n2) and tB = θ (n2)
Calculate the total computation time for the following:



Total Computation = (max (tA, tB))
                  = max (O (n2), θ (n2) = θ (n2)

3. For循环：

for循环的一般格式为：

For (initialization; condition; updation)
{
		Statement(s);
}

for循环的复杂性

外循环执行N次。每次执行外循环时, 内循环执行M次。结果, 内部循环中的语句总共执行N * M次。因此, 两个循环的总复杂度为O（N2）

考虑以下循环：

for i ← 1 to n    
 {
		 P (i)
 }

如果（PI）的计算时间ti作为“ i”的函数而变化, 则用于循环的总计算时间不是通过乘法给出, 而是通过总和即。

For i ← 1 to n    
 {
		    P (i)
 }

需要

如果算法由嵌套的“ for”循环组成, 则总计算时间为

For i ← 1 to n
 {
      For j ←  1 to n       
    {
      P (ij)
    }
 }

例：

考虑以下“ for”循环, 计算以下内容的总计算时间：

For i ← 2 to n-1
	{
		For j ← 3 to i
	     {
                       Sum ← Sum+A [i] [j]
                 }
            }

解：

总计算时间为：

4. While循环：

分析循环的简单技术是确定所涉及变量的功能, 其值每次减小。其次, 要终止循环, 必须将值设为正整数。通过跟踪函数的值减少多少次, 可以获得循环的重复次数。分析“ while”循环的另一种方法是将它们视为递归算法。

算法

1. [Initialize] Set k: =1, LOC: =1 and MAX: = DATA [1]
2. Repeat steps 3 and 4 while K≤N
3.  if MAX<DATA [k], then:
	Set LOC: = K and MAX: = DATA [k]
4. Set k: = k+1
   [End of step 2 loop]
5. Write: LOC, MAX
6. EXIT

例：

计算n个整数数组中最大元素的算法数组Max的运行时间为O（n）。

解：

array Max (A, n)
1. Current max ← A [0]
2. For i ←  1 to n-1
3. do if current max < A [i]
4. then  current max ← A [i]
5. return current max.

该算法执行的原始运算的数量t（n）至少为。

2 + 1 + n +4 (n-1) + 1=5n
2 + 1 + n + 6 (n-1) + 1=7n-2

当A [0]是最大元素时, 出现最佳情况T（n）= 5n。当元素按升序排序时, 最坏情况是T（n）= 7n-2。

因此, 我们可以使用c = 7和n0 = 1的big-Oh定义, 并得出其运行时间为O（n）。

---