给定文本txt[0..n-1]和一个模式pat[0..m-1],写一个函数search(char pat[], char
txt[])打印所有在txt[]中出现的pat[],你可以假设n > m。
例子:
输入: txt[] = "THIS IS A TEST TEXT"
pat[] = "TEST"
输出: 模式在索引10处找到
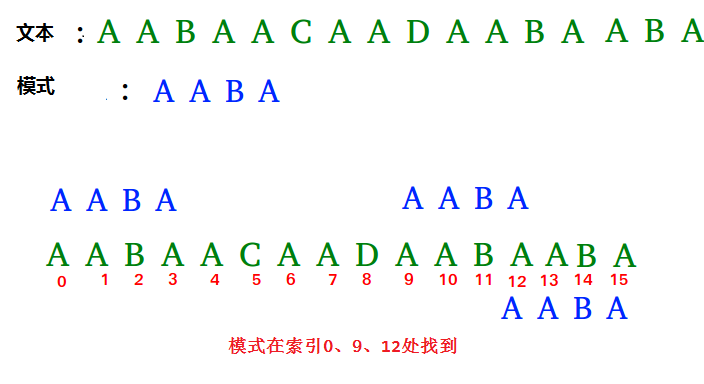
输入: txt[] = "AABAACAADAABAABA"
pat[] = "AABA"
输出: 模式在索引0处找到
模式在索引9处找到
模式在索引12处找到
简单的字符串匹配算法逐个滑动模式,在每次滑动之后,它将逐个检查当前移位处的字符,如果所有字符都匹配,则打印匹配。
和Naive算法一样,Rabin-Karp算法也会一个一个地滑动模式。但与简单算法不同的是,Rabin Karp算法将模式的哈希值与当前文本子字符串的哈希值匹配,如果哈希值匹配,则只会开始匹配单个字符。所以Rabin Karp算法需要计算下列字符串的哈希值。
- 模式本身。
- 所有长度为m的文本子串。
由于我们需要有效地计算大小为m的文本的所有子字符串的哈希值,所以我们必须有一个具有以下属性的哈希函数。
哈希在下一次移位必须是从当前哈希值和文本的下一个字符得到有效计算,或者我们可以说hash(txt[s+1 .. s+m])必须从hash(txt[s ..
s+m-1])和txt[s+m]得到,也就是hash(txt[s+1
.. s+m])= rehash(txt[s+m], hash(txt[s .. s+m-1])),重哈希必须是O(1)操作。
Rabin和Karp建议的哈希函数计算一个整数值,字符串的整数值是字符串的数值。例如,如果所有可能的字符都是从1到10,那么“122”的数值将是122。可能的字符数大于10(通常为256个),并且模式长度可能很大。因此,数值实际上不能存储为整数。因此,数值是使用模块化算法计算的,以确保哈希值可以存储在一个整数变量中(可以放入内存单词)。要进行重新哈希,我们需要去掉最有效的数字,并在哈希值中添加新的最低有效数字。重哈希是使用以下公式完成的。
- hash( txt[s+1 .. s+m] ) = ( d ( hash( txt[s
.. s+m-1]) – txt[s]*h ) + txt[s + m] ) mod q - hash( txt[s .. s+m-1]):移位s处的哈希值。
- hash( txt[s+1 .. s+m] ):下一个移位时的散列值(或移位s+1)
- d:字母表中的字符数
- q:一个质数
- h: d ^ (m – 1)
以上表达是如何工作的?
这是一个简单的数学运算,我们从以前的窗口计算当前窗口的十进制值。
例如,模式长度为3,字符串为“23456”
计算第一个窗口的值(即“234”)为234。
如何计算下一个窗口“345”的值?(234 – 2*100)*10 + 5,得到345。
C++实现Rabin-Karp模式搜索算法:
/* 下面的程序是一个c++实现的Rabin Karp算法 */
#include <bits/stdc++.h>
using namespace std;
// d是输入字母表中的字符数
#define d 256
/* pat -> pattern模式
txt -> text文本
q -> 质数
*/
void search(char pat[], char txt[], int q)
{
int M = strlen(pat);
int N = strlen(txt);
int i, j;
int p = 0; // pattern哈希值
int t = 0; // txt哈希值
int h = 1;
// h的值为 "pow(d, M-1)%q"
for (i = 0; i < M - 1; i++)
h = (h * d) % q;
// 计算模式的哈希值和文本的第一个窗口
for (i = 0; i < M; i++)
{
p = (d * p + pat[i]) % q;
t = (d * t + txt[i]) % q;
}
// 将模式一个一个地滑过文本
for (i = 0; i <= N - M; i++)
{
// 检查文本和模式当前窗口的哈希值,如果哈希值匹配,则匹配
if ( p == t )
{
/* 逐个检查字符 */
for (j = 0; j < M; j++)
{
if (txt[i+j] != pat[j])
break;
}
// if p == t and pat[0...M-1] = txt[i, i+1, ...i+M-1]
if (j == M)
cout<<"模式在索引"<< I << "处找到" <<endl;
}
// 计算下一个文本窗口的哈希值:删除前导数字,添加尾随数字
if ( i < N-M )
{
t = (d*(t - txt[i]*h) + txt[i+M])%q;
// 我们可能得到负的t,把它变成正的
if (t < 0)
t = (t + q);
}
}
}
/* 驱动代码 */
int main()
{
char txt[] = "SRCMINI FOR SRC";
char pat[] = "SRC";
int q = 101; // 质数
search(pat, txt, q);
return 0;
}
Rabin-Karp算法的平均运行时间和最佳运行时间分别为O(n+m)和O(nm)。Rabin-Karp算法最坏的情况是模式和文本的所有字符都与txt[]的所有子字符串的哈希值相同,与pat[]的哈希值匹配。例如pat[] = AAA和txt[] = AAAAAAA。