Trie树又叫做单词查找树或字典树,Trie树是一种高效的信息检索数据结构。通过使用Trie树,可以将搜索复杂度提高到最优限制(键长)。如果我们将键存储在二叉搜索树中,一个平衡良好的BST需要与M * log N成比例的时间,其中M是最大字符串长度,N是树中的键数。使用Trie树,我们可以在O(M)时间内搜索key,但是,代价是在Trie存储需求上。
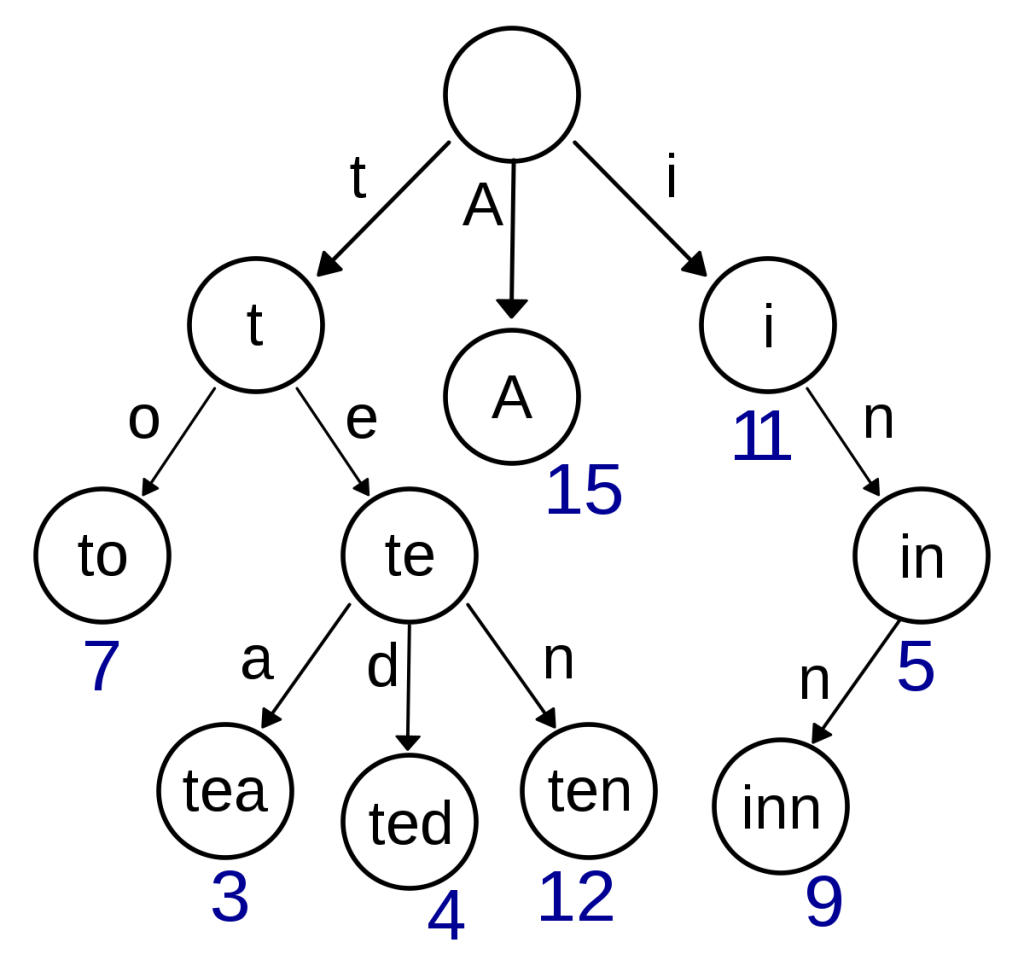
Trie树有什么用?trie树的应用如下:
1、散列:在散列中,我们将键转换为一个小值,该值用于索引数据。平均在O(L)时间内支持搜索、插入和删除操作。
2、自平衡BST:自平衡二叉搜索树(BST)(如红黑树、AVL树、Splay树等)中搜索、插入和删除操作的时间复杂度为O(llog n),其中n为总字数,L为字数长度。自平衡BSTs的优点是,他们保持有序,使操作如最小,最大,最接近和第k个最大更快。
Trie树的完整C++实现如下:
#include <iostream>
// 定义字符大小
#define CHAR_SIZE 128
// 表示Trie节点的类
class Trie
{
public:
bool isLeaf;
Trie* character[CHAR_SIZE];
// 构造函数
Trie()
{
this->isLeaf = false;
for (int i = 0; i < CHAR_SIZE; i++)
this->character[i] = nullptr;
}
void insert(std::string);
bool deletion(Trie*&, std::string);
bool search(std::string);
bool haveChildren(Trie const*);
};
// 迭代函数:在Trie中插入一个键
void Trie::insert(std::string key)
{
// 从根节点开始
Trie* curr = this;
for (int i = 0; i < key.length(); i++)
{
// 如果路径不存在,则创建一个新节点
if (curr->character[key[i]] == nullptr)
curr->character[key[i]] = new Trie();
// 转到下一个节点
curr = curr->character[key[i]];
}
// 将当前节点标记为叶子
curr->isLeaf = true;
}
// 在Trie中搜索键的迭代函数
// 如果在Trie中找到键,则返回true,否则返回false
bool Trie::search(std::string key)
{
// trie为空返回false
if (this == nullptr)
return false;
Trie* curr = this;
for (int i = 0; i < key.length(); i++)
{
// 下一个节点
curr = curr->character[key[i]];
// 如果字符串无效(在Trie中到达路径末端)
if (curr == nullptr)
return false;
}
// 如果当前节点是叶节点,并且我们已经到达了字符串的末尾,则返回true
return curr->isLeaf;
}
// 如果给定节点有任何子节点,则返回true
bool Trie::haveChildren(Trie const* curr)
{
for (int i = 0; i < CHAR_SIZE; i++)
if (curr->character[i])
return true;
return false;
}
// 在Trie中删除键的递归函数
bool Trie::deletion(Trie*& curr, std::string key)
{
if (curr == nullptr)
return false;
if (key.length())
{
if (curr != nullptr &&
curr->character[key[0]] != nullptr &&
deletion(curr->character[key[0]], key.substr(1)) &&
curr->isLeaf == false)
{
if (!haveChildren(curr))
{
delete curr;
curr = nullptr;
return true;
}
else {
return false;
}
}
}
if (key.length() == 0 && curr->isLeaf)
{
if (!haveChildren(curr))
{
delete curr;
curr = nullptr;
return true;
}
else
{
curr->isLeaf = false;
return false;
}
}
return false;
}
int main()
{
Trie* head = new Trie();
head->insert("hello");
std::cout << head->search("hello") << " "; // 1
head->insert("helloworld");
std::cout << head->search("helloworld") << " "; // 1
std::cout << head->search("helll") << " "; // 0 (Not found)
head->insert("hell");
std::cout << head->search("hell") << " "; // 1
head->insert("h");
std::cout << head->search("h"); // 1
std::cout << std::endl;
head->deletion(head, "hello");
std::cout << head->search("hello") << " "; // 0
std::cout << head->search("helloworld") << " "; // 1
std::cout << head->search("hell"); // 1
std::cout << std::endl;
head->deletion(head, "h");
std::cout << head->search("h") << " "; // 0
std::cout << head->search("hell") << " "; // 1
std::cout << head->search("helloworld"); // 1
std::cout << std::endl;
head->deletion(head, "helloworld");
std::cout << head->search("helloworld") << " "; // 0
std::cout << head->search("hell") << " "; // 1
head->deletion(head, "hell");
std::cout << head->search("hell"); // 0
std::cout << std::endl;
if (head == nullptr)
std::cout << "Trie empty!!\n"; // empty
std::cout << head->search("hell"); // 0
return 0;
}