在上一篇文章:数据结构、算法分析、算法复杂度、大O符号中有提到数据结构有三种基本结构形式:集合结构、线性结构、树形结构、图状或网状结构,更形象的解析是结点和结点之间的逻辑关系,例如一对一关系为线性结构,而一对多关系为树形结构,有过数据表设计经验的朋友一定对这个很熟悉,这就是为什么一般程序员都是在做增删改查了。数据结构以逻辑结构分类,可分为线性结构非线性结构,经典线性结构包括线性表、栈和队列,非线性结构有树和图,本节重点讲解线性结构,注意这是逻辑结构分类的叫法。而另一种是以数据在内存中的存储结构进行分类,可分为顺序结构、链式结构、索引结构和哈希结构。
本节相关内容在C语言教程高级数据结构和算法详解中有更基本和详细的讲解,可参考获取更多有用的信息。
一、抽象数据类型(Abstract Data Type)
我们知道程序由数据结构和算法组成,这是说一个程序可能含有大量的数据结构和算法,而抽象数据类型(简称ADT)则是一个其中的一个基本单元,也就是说一个程序是有一个或多个ADT组成的。什么是抽象数据类型ADT呢?ADT即数据结构+算法,ADT实际上就类似于基本数据类型(如整型、浮点型)+算术操作,ADT是比基本数据类型包含更多数据的一种类型,例如链表、二叉树、栈+相关的算法操作,算法操作例如增删改查,集合结构有并和交的操作,所以当我们在说抽象数据类型或ADT时,说的就是数据结构+算法。
数据结构指的是数据的组织方式,包含结点数据和逻辑关系,在代码上设计一个数据结构的时候,至少要包含数据域、结点及结点间的逻辑关系,以及ADT主要接口,详细的内容在上一篇文章中有解释,对数据结构的理解比较重要,这涉及到我们设计程序的时候对数据模型的合理选择。
算法是对某一问题的具体求解方法,包括算法设计、算法分析和算法证明,这里解释一下分治算法,分治算法是对某一问题的整体分析,并不是一个具体的算法,它主要用于分析问题,如下图:

将问题规模为N分解成k个相同或相似的子问题,上面根据数据结点特点划分只是其中一个建议,到子问题的时候才是真正选择具体求解算法,一般这里可以很容易写成递归的形式。
下面说一下ADT代码设计的一个建议规范格式,在设计数据结构的时候,需要考虑逻辑结构和存储结构,ADT的设计包含是数据结构和算法,主要包含:
1、数据域Data,实际的业务数据模型;
2、结点Node,数据结构的基本数据单元,结点成员包含数据域Data,以及结点间的逻辑关系,有的地方可能会看到将数据域和结点写成一个整体;
3、ADT对外接口,整个ADT数据对象的对外体现,成员包含基本结点信息,以及一些额外信息,如ADT的大小,二叉树ADT的根结点等。
下面是一个完整的例子:
// 数据结构的主要表示
// 数据域,抽象业务数据
typedef struct data{
int price;
int weight;
} Data;
// 结点,基本数据单元,这里是一个链表的结点形式
typedef struct node{
Data data; // 结点的数据域
struct node *next; // 下一个结点的指针
} Node;
// ADT对外接口,ADT对象的主要持有者
typedef struct list{
Node *head; // 头结点
Node *tail; // 尾结点
unsigned int size; // ADT的大小
} List;
// 算法
// 创建一个空List,并进行初始化
extern List *list_init();
// 添加一个结点到指定位置
extern int list_add(List *list, Data *data, unsigned int position);
// 清空所有结点
extern int list_clear(List *list);
二、线性表(List)
线性表的基本形式为:a1,
a2, …, aN,N为表的大小,N=0为空表,ai为结点,以索引i=0为表最前,ai的后继元为ai+1,ai的前驱为ai-1。线性表根据数据的存储结构有两种方式:顺序结构和链式结构,称为顺序表和链表。
1、顺序表ADT(Sequence
List)

顺序表即数组,数组的形式又有栈数组和堆数组,栈数组指表在栈内存中存储,堆数组则是在堆内存中存储。顺序表的大小固定,过大可能浪费空间,过小可能空间不足,顺序表在查找数据上相对较好,为O(N),但是在增加、删除、修改数据较差,最坏情况为O(N)。在设计顺序表ADT时要注意按照上面建议的ADT风格设计,对于顺序表,ADT接口至少要提供表的首地址,下面是图书顺序表ADT的完全声明:
// 图书数据元素/数据域
typedef struct book{
unsigned int id;
char title[256];
char author[128];
} Book;
// 结点声明省略,直接使用数据域作为结点,除非有更复杂的需求添加指针域或其它
//typedef struct ele{
// Book book;
//} Ele;
// 顺序表ADT对外接口
typedef struct seqlist{
Book *books[MAX_SIZE];
unsigned int size;
unsigned int max_size;
} SeqList;
// 创建并初始化SeqList
extern SeqList* seqlist_init();
// 检查顺序表是否为空
extern int seqlist_is_empty(SeqList *seqList);
// 检查顺序表是否已满
extern int seqlist_is_full(SeqList *seqList);
// 在表指定索引位置添加结点,index=0默认在末尾添加
extern int seqlist_add(SeqList *seqList, Book *book, unsigned int index);
// 根据Book的id获取结点数据
extern Book* seqlist_get(SeqList *seqList, unsigned int id);
// 根据id删除结点数据
extern int seqlist_delete(SeqList *seqList, unsigned int id);
// 清空顺序表
extern int seqlist_clear(SeqList *seqList);
以上算法声明都是一些经常需要的操作,例如初始化、判断是否为空、是否已满等,对于顺序表ADT对外接口,可以typedef声明一个指针别名,在实现接口的时候要仔细参数的正确性,复杂的算法需要画一下执行流程图或画图分析数据结构,下面是接口的实现代码:
// 创建并初始化SeqList
SeqList* seqlist_init(){
SeqList *seqList = (SeqList*)malloc(sizeof(SeqList));
if(!seqList){
perror("init seqlist failed.");
return NULL;
}
seqList->size = 0;
seqList->max_size = sizeof(seqList->books) / sizeof(seqList->books[0]);
return seqList;
}
// 检查顺序表是否为空
int seqlist_is_empty(SeqList *seqList){
return seqList == NULL || seqList->size == 0;
}
// 检查顺序表是否已满
int seqlist_is_full(SeqList *seqList){
return seqList->size == seqList->max_size;
}
// 在表指定索引位置添加结点,index=0默认在末尾添加
/**
* seqlist = NULL, FULL
* book = NULL
* index < 0,
* index = 0
* index < max_size
* index > size
* */
int seqlist_add(SeqList *seqList, Book *book, unsigned int index){
if(seqList == NULL || seqlist_is_full(seqList) || book == NULL || index > seqList->max_size - 1 || index < 0)
return -1;
Book *data = (Book*)malloc(sizeof(Book));
if(!data){
perror("init data failed.");
return -1;
}
data->id = book->id;
strcpy(data->title, book->title);
strcpy(data->author, book->author);
if(index == 0 || index >= seqList->size){
seqList->books[seqList->size] = data;
seqList->size++;
return 1;
}
for (int i = seqList->size; i > index; --i) {
seqList->books[i] = seqList->books[i - 1];
}
seqList->books[index] = data;
seqList->size++;
return 1;
}
// 根据Book的id获取结点数据
Book* seqlist_get(SeqList *seqList, unsigned int id){
if(seqlist_is_empty(seqList))
return NULL;
for (int i = 0; i < seqList->size; ++i) {
if(seqList->books[i]->id == id)
return seqList->books[i];
}
return NULL;
}
// 根据id删除结点数据
int seqlist_delete(SeqList *seqList, unsigned int id){
if(seqlist_is_empty(seqList))
return -1;
for (int i = 0; i < seqList->size; ++i) {
if(seqList->books[i]->id == id){
for (int j = i; j < seqList->size - 1; ++j) {
seqList->books[j] = seqList->books[j + 1];
}
seqList->books[seqList->size - 1] = NULL;
seqList->size--;
return 1;
}
}
return -1;
}
// 清空顺序表
int seqlist_clear(SeqList *seqList){
for (int i = 0; i < seqList->size; ++i) {
free(seqList->books[i]);
}
free(seqList);
return 1;
}
顺序表的添加和删除数据通过左右移动结点实现,为O(N)比较费时,写好的算法需要根据参数条件证明算法的正确性,可结合调用实例调试算法,主要是改变不同的参数输入进行测试,多方面的测试可保证算法的健壮性,下面是顺序表ADT的使用示例:
SeqList *seqList = seqlist_init();
printf("size: %u, max size: %u\n", seqList->size, seqList->max_size);
Book b1;
b1.id = 5;
strcpy(b1.title, "The Price of Salt");
strcpy(b1.author, "Highsmith");
Book b2;
b2.id = 6;
strcpy(b2.title, "The Old Man and The Sea");
strcpy(b2.author, "Hemingway");
Book b3;
b3.id = 3;
strcpy(b3.title, "One Hundred Years of Solitude");
strcpy(b3.author, "Garcia");
seqlist_add(seqList, &b1, 0);
seqlist_add(seqList, &b2, 3);
seqlist_add(seqList, &b3, 1);
for (int i = 0; i < seqList->size; ++i) {
printf("%s\n", seqList->books[i]->title);
}
putchar('\n');
printf("%s\n", seqlist_get(seqList, 3)->title);
seqlist_delete(seqList, 5);
putchar('\n');
for (int i = 0; i < seqList->size; ++i) {
printf("%s\n", seqList->books[i]->title);
}
seqlist_clear(seqList);
2、链表ADT(Linked
List)
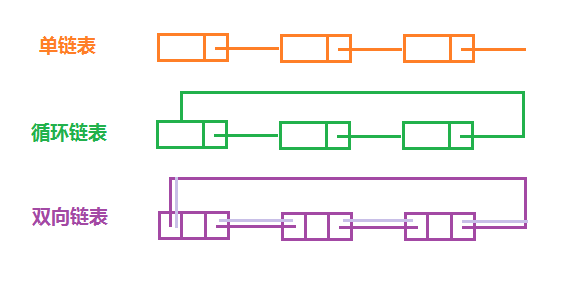
链表的结点数据使用链式结构进行储存,每个结点存储下一个后继结点的指针,链表有三种基本形式,如上图,单链表的所有结点单向链接,最后结点的指针成员值为NULL;双向链表的每个结点存储前后结点的指针,第一个和最后一个结点可互相指向,又称为双向循环链表,双向链表会增加空间开销,增加操作数据的开销,但是可以简化删除操作;循环链表的最后一个结点的指针成员指向头结点,循环链接。
链表相对线性表,增加、删除结点的操作较好,最好为O(1),但是查找较慢为O(N)。在设计链表ADT时,对外ADT接口只要需要提供表头指针。
下面使用链表实现一元多项式函数ADT,例如x^2+x+3,将多项式的每一项作为一个结点储存,结点主要储存每一项的系数和指数,提供的功能操作算法有加减乘、导数/微商和不定积分和定积分,首先看ADT的声明代码:
/**
* 实现多项式ADT
* a0*X^n + a1*X^(n-1) + ... + an-1*X
* 主要存储ai系数和n指数
* */
// 多项式的每一项表达式
typedef struct expression{
float coefficient; // 系数
float exponent; // 指数
} Expression;
// 多项式项结点
typedef struct item{
Expression expression;
struct item *next;
} Item;
// 多项式ADT对外接口,使用单链表实现
typedef struct polynomial{
Item *head; // 头结点
Item *tail; // 尾结点
unsigned int size; // 多项式的项数
} Polynomial;
/**
* 单个多项式自身的运算,包括初始化、检查是否空或已满、添加表达式、获取单项、清除数据
* */
extern Polynomial* poly_init();
extern int poly_is_empty(Polynomial *polynomial);
extern int poly_is_full(Polynomial *polynomial);
extern int poly_add(Polynomial *polynomial, Expression *expression);
extern Expression* poly_get(Polynomial *polynomial, float exponent);
extern int poly_delete(Polynomial *polynomial, float exponent);
extern int poly_clear(Polynomial *polynomial);
/**
* 多项式的运算:多项式相加、相减、相乘
* 单个多项式求导数/微商、积分(定积分和不定积分)
* */
extern Polynomial* poly_plus(Polynomial *poly1, Polynomial *poly2);
extern Polynomial* poly_subtract(Polynomial *sub1, Polynomial *sub2);
extern Polynomial* poly_multiply(Polynomial *poly1, Polynomial *poly2);
extern Polynomial* poly_differential(Polynomial *poly);
extern Polynomial* poly_in_integral(Polynomial *poly);
extern float poly_integral(Polynomial *poly, float lower, float upper);
// 计算多项式的代数值
extern float poly_algebraic_value(Polynomial *poly, float value);
// 以字符串的形式输出多项式代数式
extern char* poly_algebraic_expression(Polynomial *poly);
由于实现和调用代码过长,这里就不贴过多的代码了,需要查看或获取完整的代码请查看github项目:https://github.com/onnple/polynomial,该项目提供多项式函数的基本运算:加减乘、导数/微商、不定积分和定积分运算。
三、栈(Stack)
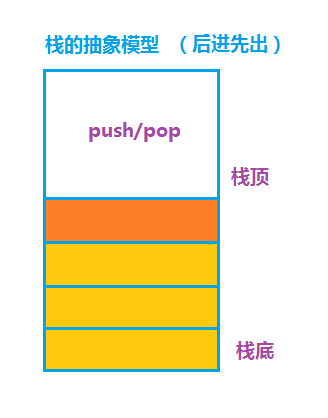
栈是一种先进后出的表,表的最前端称为栈底,尾端称为栈顶,它限制删除和插入的操作只在表的一个位置上,即栈顶的位置。栈顶是表的末尾,入栈和出栈的位置,栈底是表的头部,栈的最基本操作是入栈push和出栈pop。
栈ADT的实现接口中至少要提供栈顶和栈底,实现方式也有两种:顺序表和单链表,这两种方式操作都很方便,数据较小的情况下使用顺序表数组会更方便。栈是一种很简单的数据结构,但是非常有用,例如我们的程序代码在栈内存中执行,和栈数据结构的操作是一样的,下面是使用双向链表实现的栈ADT的声明,该例子是C语言实现一个简单的语法检查器和进制转换器,栈ADT至少要提供栈顶和栈底:
// 字符,栈数据结点
typedef int SData;
typedef struct snode{
SData data;
struct snode *prev;
struct snode *next;
} SNode;
// 语法检查栈ADT对外接口
typedef struct stack{
SNode *top;
SNode *bottom;
unsigned int size;
} Stack;
extern Stack* stack_init();
extern int stack_is_tempty(Stack *stack);
extern int stack_is_full(Stack *stack);
extern int stack_push(Stack *stack, const SData* data);
extern SData stack_pop(Stack *stack);
extern SData stack_peek(Stack *stack);
extern int stack_clear(Stack *stack);
// 语法检查
extern int syntax_auth(const char str[], int len);
// 进制转换
extern char* to_base_str(int value, int base);
在这里,栈ADT相当于数据容器,在面向对象编程如Java中,数据结构类是充当数据容器对象,可以使用void指针实现面向对象中添加不同类型的数据,这种ADT可作为通用ADT,但在操作细节上相对较难,而特定情况的ADT则比较直接,而且可以在细节上访问,下面是详细的实现细节:
Stack* stack_init(){
Stack *stack = (Stack*)malloc(sizeof(Stack));
if(!stack){
perror("init stack failed.");
return NULL;
}
stack->top = NULL;
stack->bottom = NULL;
stack->size = 0;
return stack;
}
int stack_is_tempty(Stack *stack){
return stack->size == 0;
}
int stack_is_full(Stack *stack){
SData *data = (SData*)malloc(sizeof(SData));
if(!data)
return 1;
Free(data);
return -1;
}
int stack_push(Stack *stack, const SData* data){
if(stack == NULL || data == NULL)
return -1;
SNode *sNode = (SNode*)malloc(sizeof(SNode));
if(!sNode){
perror("init data failed.");
return -1;
}
memset(sNode, 0, sizeof(SNode));
sNode->data = *data;
sNode->next = NULL;
sNode->prev = NULL;
if(stack->size == 0){
stack->top = sNode;
stack->bottom = sNode;
stack->size++;
return 1;
}
stack->top->next = sNode;
sNode->prev = stack->top;
stack->top = sNode;
stack->size++;
return 1;
}
SData stack_pop(Stack *stack){
SNode *node = stack->top;
SData data = node->data;
stack->top = node->prev;
free(node);
stack->size--;
return data;
}
SData stack_peek(Stack *stack){
if(stack == NULL || stack->size == 0)
return -1;
return stack->top->data;
}
int stack_clear(Stack *stack){
if(stack == NULL)
return -1;
SNode *node = stack->bottom;
while(node){
SNode *temp = node->next;
free(node);
node = temp;
}
free(stack);
return 1;
}
// 语法检查: {} [] ()
int syntax_auth(const char str[], int len){
Stack *stack = stack_init();
if(!stack)
return -1;
for (int i = 0; i < len; ++i) {
SData data = str[i];
if((stack_peek(stack) == '{' && data == '}') ||
(stack_peek(stack) == '[' && data == ']') ||
(stack_peek(stack) == '(' && data == ')'))
stack_pop(stack);
else
stack_push(stack, &data);
}
int result = stack->size == 0 ? 1 : -1;
stack_clear(stack);
return result;
}
// 进制转换 base < 10
char* to_base_str(int value, int base){
if(value < 0 || base <= 0 || base >= 10)
return NULL;
if(value == 0)
return 0;
Stack *stack = stack_init();
if(!stack)
return NULL;
int number = 0;
while(value > 0){
number = value % base;
stack_push(stack, &number);
value = value / base;
}
char *str = (char *)malloc(stack->size * sizeof(char) + 1);
memset(str, 0, stack->size * sizeof(char) + 1);
int len = stack->size;
char temp[1];
for (int i = 0; i < len; ++i) {
sprintf(temp, "%d", stack_pop(stack));
strcat(str, temp);
}
*(str + len) = '\0';
stack_clear(stack);
return str;
}
以下是文本语法检查和进制调用的实际调用,进制范围为0~9,相对还算简单。上面的代码基本都有根据应用的实现,由此你可以发现,一个完整的程序就是这样写的,先写清楚需求,然后从需求中抽象出数据结构,不同的需求有不同的数据结构,之后就是完整的ADT实现,多个ADT就组成了一个完整的程序。写程序就是在写ADT,可能有些ADT的数据结构比重较轻,数据简单或直接没有。
四、队列(Queue)
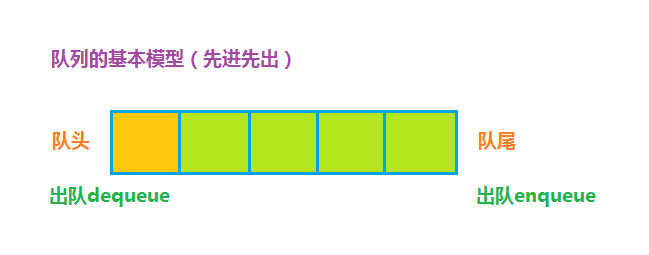
队列是一种先进先出的表,队列有队头和队尾,入队Enqueue表示从队尾插入数据,出队Dequeue表示从队头删除数据。队列是一种相当简单的数据结构,但是非常有用,比如你可能听过的消息队列、任务队列等,设计队列ADT至少需要提供队头和队尾,实现方式根据顺序存储和链式存储也有两种方式:顺序表和链表,这里使用链表实现队列ADT,实现一个任务队列,如果你学过JavaScript,应该都知道JavaScript事件循环机制,其中就有任务队列,在主线程执行完后到任务队列获取任务执行,下面是任务队列ADT的声明部分:
// 任务队列ADT声明
// 任务数据域
typedef void (*Task)(void);
// 任务结点
typedef struct tnode{
Task task;
struct tnode *next;
} TNode;
// 任务队列ADT
typedef struct queue{
TNode *head;
TNode *tail;
unsigned int size;
} Queue;
extern Queue* queue_init();
extern int queue_is_empty(Queue *queue);
extern int queue_is_full(Queue *queue);
extern int queue_enqueue(Queue *queue, Task task);
extern Task queue_dequeue(Queue *queue);
extern int queue_clear(Queue *queue);
extern int queue_execute_tasks(Queue *queue);
任务队列ADT中,使用函数指针表示一个任务,其它结构和一般的队列结构没什么不同,最基本的还是对链表的操作,建议多使用链式结构,很多高级的数据结构都是使用链式结构实现的,实际上很多你需要的数据结构都可以使用链式结构,链式结构的一个特点使用malloc和指针,下面是任务队列ADT的实现代码:
Queue* queue_init(){
Queue *queue = (Queue*)malloc(sizeof(Queue));
if(!queue){
perror("init queue failed.");
return NULL;
}
queue->head = NULL;
queue->tail = NULL;
queue->size = 0;
return queue;
}
int queue_is_empty(Queue *queue){
return queue->size == 0;
}
int queue_is_full(Queue *queue){
TNode *node = (TNode*)malloc(sizeof(TNode));
if(!node)
return 1;
free(node);
return -1;
}
int queue_enqueue(Queue *queue, Task task){
if(queue == NULL || task == NULL)
return -1;
TNode *node = (TNode*)malloc(sizeof(TNode));
if(!node)
return -1;
node->task = task;
node->next = NULL;
if(queue->size == 0){
queue->head = node;
queue->tail = node;
queue->size++;
}
queue->tail->next = node;
queue->tail = node;
queue->size++;
return 1;
}
Task queue_dequeue(Queue *queue){
if(queue == NULL || queue->size == 0)
return NULL;
TNode *node = queue->head;
queue->head = node->next;
Task task = node->task;
free(node);
return task;
}
int queue_clear(Queue *queue){
if(queue == NULL)
return -1;
TNode *node = queue->head;
while(node){
TNode *temp = node->next;
free(node);
node = temp;
}
free(queue);
return 1;
}
int queue_execute_tasks(Queue *queue){
if(queue == NULL)
return -1;
TNode *node = queue->head;
while(node){
TNode *temp = node->next;
(node->task)();
free(node);
node = temp;
}
queue->head = NULL;
queue->tail = NULL;
queue->size = 0;
return 1;
}
下面是任务队列ADT的使用,任务队列和消息队列在很多应用中都有,例如一些常见的消息队列中间件ActiveMQ、RabbitMQ、RocketMQ和Kafka,基本原理也是基于队列数据结构。
void task1(void){
printf("01 processing the result of ajax......\n");
}
void task2(void){
printf("02 rendering the data of elements......\n");
}
void task3(void){
printf("03 execute the task of timeout......\n");
}
void queue(void){
Queue *queue = queue_init();
queue_enqueue(queue, task3);
queue_enqueue(queue, task1);
queue_enqueue(queue, task2);
Task task = queue_dequeue(queue);
task();
queue_execute_tasks(queue);
queue_clear(queue);
}