程序由数据结构和算法组成,也是程序设计最难的部分,特别是算法设计实现的部分。在面向对象编程语言中可能相对有一些人不甚注意,因为这些语言提供了一些数据结构和算法的实现,但是实现复杂程序依然难以下手。我们需要明白,程序设计就是简单地和数据结构和算法打交道,不管是否使用现成库实现都需要有这个概念,否则设计程序就失去了方向感。
本节重点介绍数据结构和算法的基本概念,相关的内容相当重要,例如对数据结构的理解,如何进行算法分析,如何描述算法复杂度,如时间复杂度和空间复杂度,什么是大O符号,如何进行算法设计等等。
既然是进阶,内容就有一些难度,这里尽量更形象描述,以前看过一些关于数据结构和算法的书籍,普遍有两个问题:内容布局条理性不好,如果你阅读没有整合的习惯就容易分散;伪代码看着难受,没有直观的算法描述,这个问题最苦恼,我们在设计算法需要对算法有一个描述,否则随意想就不成标准。
本节及之后的内容以之前C教程的内容为基础,可参考:C语言高级数据结构和算法详解。
一、数据结构
数据结构主要分析数据及其之间的逻辑关系,我们根据实际需求抽象出数据结构,不同的需求选择合适的数据结构,我们说数据结构意思就包括了数据项和数据项之间的逻辑关系,下面即系更详细的介绍。
数据元素:数据元素是整个数据结构对象中的最小数据单元,又在C语言中一般使用一个结构体表示,在高级语言中可用一个Object表示,结构体的成员又称为数据项,数据元素又可称为数据结构中的基本数据单元。
数据结构:描述存在特定关系的数据元素的集合,即数据元素+逻辑关系,简单可表示为A-B-C-D-E,下图是更形象的描述:
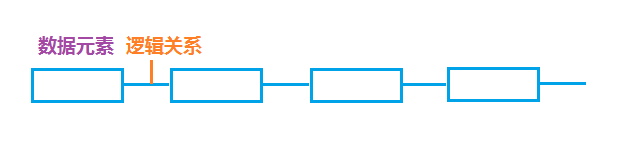
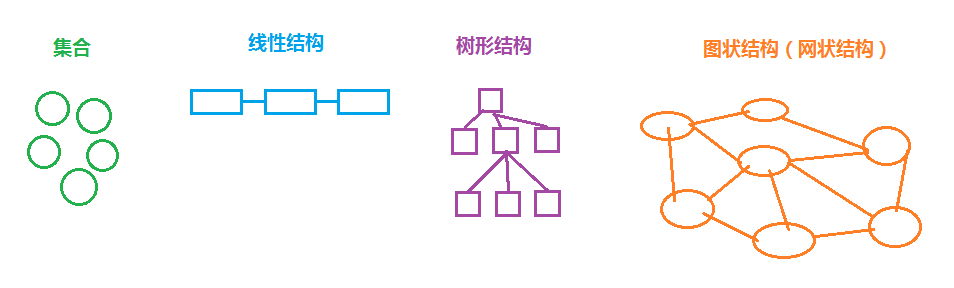
也就是给出几个数据单元,我们可以根据不同的逻辑关系构造出不同的数据结构,一般来说有四种基本数据结构(可参考数据表设计中的概念):
1、集合结构,数据元素属于自身集合,数据元素之间没有关系。
2、线性结构,数据元素是一对一的关系。
3、树形结构,数据元素是一对多的关系。
4、图状结构(网状结构),数据元素是多对多的关系。
下图是更形象的描述:
另外还有几个概念需要解释一下:
结点:数据元素的另一种称呼,结点会更常用到。
数据域:数据元素中的数据项,强调数据元素中的数据项,这个称呼也更常用到。
下面是一个数据结构的具体代码的例子:
// 数据项,数据域
typedef struct d{
int a;
int b;
} Data;
// 数据结点,数据元素
typedef struct n{
Data data; // 数据项,数据域
struct n *left; // 体现了树形数据结构,一对多的关系
struct n *right;
} Node;
// 数据结构对象主要接口
typedef struct t{
Node *root;
unsigned int size;
} Tree;
在数据的物理存储上,存储数据的结构成为存储结构,一般来说有两种存储结构,顺序存储和非顺序存储,以上概念一般来说如果你基本掌握语言本身的知识,理解一般都是没有问题的,关于数据结构的详细内容之后的章节会详细介绍,下面详细介绍算法。
二、算法
针对某一需求,算法是对于某一问题的具体计算方法,整体表现为一个函数,函数体由一条指令或多条指令组成,所有这些指令称为问题的求解步骤。所以写一个函数,写一些简单的执行语句组成的函数也是一个算法。
1、设计算法
(1)描述问题:清晰地描述一个需求问题是实现算法的重要一步,一般来说,如果能很好地描述一个问题,那么接着就可以有一个大概的解法了。描述问题这里,首先要确定数据集Q,数据集的大小N,又称为数据长度或问题规模,然后使用自然语言写下求解问题的简要描述。
(2)确定求解算法,对于一个问题的求解算法,很难说可以有一个直接切入的方式。但是有一个大概的求解方向,目前有几种方式可以供我们选择,这些方式是分析问题的主要参考方法,比如常见的有:分治算法、动态规划法、贪心算法、回溯法和分支界限法,之后的章节会有更多的详细内容,这里仅做简要介绍。
(3)算法的表示方式,使用自然语言描述,包括输入参数说明,主要执行步骤说明,输出结果说明等。另一种方式则是使用流程图,开始、中间执行步骤、结束等。
以上设计算法的步骤并不是一个标准参考手册,不过就目前来说,设计算法时参考以上方式会更好,例如使用自然语言描述问题和算法求解过程,还有算法的流程图表示方式,这个方式比伪代码会好很多,还有些地方甚至没伪代码,给出算法然后一步一步分析,这绝对不是一个好方法!开始也有想到使用数学函数和集合来表示算法,但是如果不是计算数值问题则很难对应到程序实现上来。另外,算法最终还是要靠自己思考和写或参考别人的写法,写多了自然有不错的算法敏感度。
这里给出该设计算法方法的一个实例:
/**
* (1)问题描述:
* 找出一个数组中首次出现次数最高的数字,并输出该数字
* 数组Q,问题规模N
* (2)求解算法:
* 先将数组Q的每个元素Q(i)和Q中所有元素比较,计算出每个元素出现的次数,
* 将每次计算的次数和最大次数比较,保留高次数的值和索引
* */
// 这里算法复杂度为O(N^2)
int most(const int array[], int len){
int index = -1, max_times = 0;
for (int i = 0; i < len; ++i) {
if(index == i) // 这里可稍微降低执行次数
continue;
int times = 0;
for (int j = 0; j < len; ++j) {
if(array[i] == array[j])
times++;
}
if(times > max_times){
index = i;
max_times = times;
}
}
return array[index];
}
void basic_print(void){
int arrays[SIZE] = {7, 2, 13, 7, 8, 13, -9, 7, 16};
int number = most(arrays, SIZE);
printf("\nmost: %d\n", number);
}
下面使用流程图表示以上实现的算法,该流程图相对粗略,但是基本能表示出该算法的主要解法,若要更标准可使用Visio:
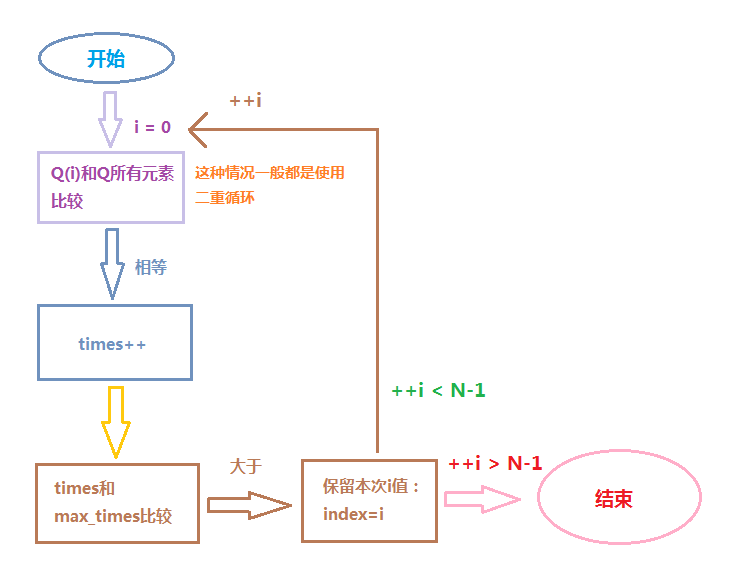
使用流程图或自然语言描述算法相当有用,特别是递归算法,手动画算法流程图也是个不错的选择,显得特有逼格,比如下图这样,简直666。
2、算法分析
算法分析是算法中的一个重点内容,涉及到我们对一个算法的把握程度,一个算法的好坏判断,算法的优化等。
(1)算法的输入输出
这个在上面已有提及,首先算法处理的问题数据集为Q,表示输入的数据,N为问题规模,即数据长度,算法输出计算结果与Q有关。
(2)算法复杂度
算法复杂度主要用来衡量一个算法的好坏,算法复杂度又分为时间复杂度和空间复杂度,意思就是执行一个算法CPU使用的时间有多长,使用的RAM内存空间有多大,另外宽带也会影响算法的效率,空间复杂度主要与输入数据集Q内存大小和算法执行所用的空间大小有关,我们主要讨论时间复杂度,一般说算法复杂度也是指时间复杂度,算法复杂度大小是一个关于输入的问题规模N的数学函数。
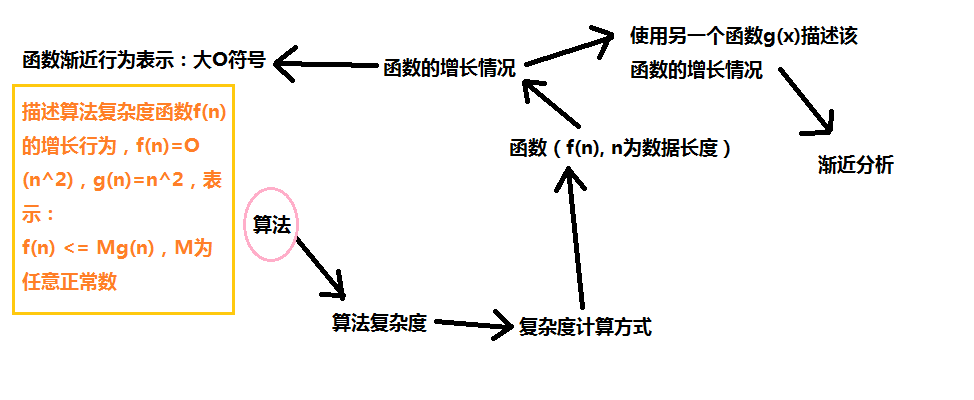
一般书上的数学定义都是很复杂的,如下图:

这里有两个函数T(N)和f(N),T(N)表示算法复杂度,f(N)是另一个函数,该函数用来描述T(N)的渐近行为。大O表示法表示f(N)是T(N)的渐近上限,算法执行的最坏情况;大Ω表示法表示f(N)是T(N)是渐进下限,算法执行的最好情况;大Θ表示法表示f(N)等于T(N)增长率,算法执行的平均情况;小o表示法表示T(N)的增长率远小于f(N)的增长率。
算法复杂度一般使用大O符号的记法,表示算法执行的最坏情况,记为:T(N)=O(f(N)),平时我们直接写为O(f(N))。关于以上的数学定义,若要更准确的理解则需要有极限的基础,大O记法实质表示,当N趋于无穷大的时候,f(N)/T(N)的极限为一个常数,平时分析也会将N当做趋向无穷大处理,关于大O符号的引入可参考下图:
T(N)的计算方式
T(N)是算法的实际运行时间,首先我们知道一个算法整体体现为一个函数,函数又语句组成,我们并不知道一个语句的准确运行时间,但是我们可以称执行一个基本语句所用时间为一个时间单元,也就是执行一条指令计为1个时间单元。如果一个函数执行1个语句,那么该算法的复杂度可记为O(1),实际上执行常数个数据也记为O(1)。不过我们更关心那些与问题规模N有关的执行语句,如一个N次的for循环复杂度为O(N)。
基本计算规则为:
一次执行为一个时间单元,例如赋值、算术运算、布尔逻辑和位运算等;
if和switch条件语句,条件表达式执行时间 + 最长条件语句块的执行时间;
for和while循环语句,语句执行时间 x 迭代次数。
计算f(N)的方法:
保留f(N)最高阶项,省略其它项;
省略f(N)的系数。
例如:计算得到一个算法的T(N)=1+2N+N^2,则f(N)=N^2,即:T(N)=O(N^2),在实际中我们也不需要细节地计算T(N),只需要找到与N有关的执行语句即可快速得到f(N),不过若是不大明白也可仔细计算一下。
f(N)并不能计算实际的运行时间,它只是对算法效率的一种渐近描述,若要计算程序算法的实际运行时间,则需要使用语言本身提供的时间戳API,例如C中可用time()函数,java中可使用System.currentTimeMillis()。
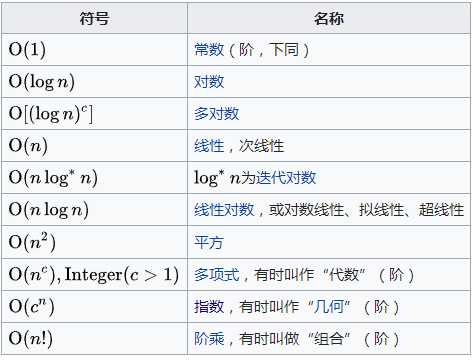
(3)常见复杂度及示例代码
常见的算法复杂度如下图:
下面是围绕求最大子序列和的问题,采用不同的算法复杂度实现的算法,重点的算法可参考注释说明:
#define SIZE 9
/**
* 求最大子序列和
* 输入数据:Q(N)={x1, x2, x3, ... xN}
* N:问题规模,即输入数据长度
* 求解问题描述:Max(n,m) = Q(n)+...+Q(m), n<=N,m<=N,n<=m
* */
// 时间复杂度为:O(N^3)
int max_sum_01(const int array[], const int len){
int max = 0;
for (int i = 0; i < len; ++i) {
for (int j = i; j < len; ++j) {
int count = 0;
for (int k = i; k <= j; ++k) {
count = count + array[k];
}
if(count > max)
max = count;
}
}
return max;
}
// 时间复杂度为:O(N^2)
int max_sum_02(const int array[], const int len){
int max = 0;
for (int i = 0; i < len; ++i) {
int count = 0;
for (int j = i + 1; j < len; ++j) {
count = count + array[j];
int temp = count + array[i];
if(temp > max)
max = temp;
}
}
return max;
}
// 时间复杂度为:O(N logN)
/**
* 分治算法:将问题细分求解
* 问题:求子序列和的最大值,关于问题规模N
* 将序列Q(n)分成左中右三部分,分别求出这三部分中的最大值即为解
* 语言演绎法叙述求解算法:
* 中间最大值:计算中点位置center,以center为中心,向左向右求出最大值n1和n2,中间的最大值为n1+n2
* 左边最大值:以0~center为新序列,计算中心位置center1。。。(和以上描述相同,即存在调用自身的情况)
* 左右最大值通过求中间最大值的递归方式求得
* */
int max(int center, int left, int right){
if(center > left){
if(center > right)
return center;
else
return right;
}
else{
if(left > right)
return left;
else
return right;
}
}
int max_center(const int array[], const int left, const int right){
if(left == right) // 递归的基本条件
return array[left];
int center = (left + right) / 2;
// 计算中间部分左边最大值
int left_sum_max = 0, left_sum = 0;
for (int i = center; i >= left; --i) {
left_sum += array[i];
if(left_sum > left_sum_max)
left_sum_max = left_sum;
}
// 计算中间部分右边最大值
int right_sum_max = 0, right_sum = 0;
for (int j = center + 1; j <= right; ++j) {
right_sum += array[j];
if(right_sum > right_sum_max)
right_sum_max = right_sum;
}
// 中间部分最大值:复杂度为N,计算中间值为高频率执行
int center_max = left_sum_max + right_sum_max;
// 左边部分最大值: 复杂度为N logN,递归调用logN次,每次递归计算一次中间值(N)
int left_max = max_center(array, left, center);
// 右边部分最大值:复杂度为N logN
int right_max = max_center(array, center + 1, right);
return max(center_max, left_max, right_max);
}
int max_sum_03(const int array[], const int len){
return max_center(array, 0, len - 1);
}
// 时间复杂度为:O(N)
int max_sum_04(const int array[], const int len){
int max = 0;
int count = 0;
for (int i = 0; i < len; ++i) {
count += array[i];
if(count > max)
max = count;
else if(count < 0)
count = 0;
}
return max;
}
void basic_print_01(void){
int arrays[SIZE] = {2, 3, -9, 8, -3, 7, 6, -10, 5};
int sum01 = max_sum_03(arrays, SIZE);
int sum02 = max_sum_04(arrays, SIZE);
printf("max: %d\n", sum01);
printf("max: %d\n", sum02);
}
(4)算法分析实例
进行算法分析时,主要考虑问题规模N,时间复杂度O(f(N)),算法实现。一般来说,优先考虑的算法是O(1),然后是O(logN)、O(N)、O(N logN)和O(N^2),N^3以上的算法都很慢了。另外还要考虑空间复杂度,比较明显的例子是递归算法,递归算法会消耗较多的内存空间,可以转为while循环。
分治算法和递归算法:什么是分治算法?将问题分而治之,如果一个问题可以通过分解成k个相同的问题,通过分别求解这k个问题,将得到的解进行合并,得到最终解,则这种算法称为分治算法。
什么是递归算法?递归即传递和归来,使用自身来定义的算法(或函数)称为递归算法,递归算法需要有结束条件,例如: F(X)=F(X-1)+2X, F(0)=5,这个函数计算需要执行X次相同的操作,写成代码如下:
int f(int x){
if(x == 0)
return 5;
else
return f(x - 1) + 2 * x;
}
只要明白上面递归算法的定义,递归算法在进行数值计算的时候是比较容易写的,例如斐波那契数列,但是多数情况都是非数值计算,这时候就会出现“神用递归,人用迭代“,那么我们该如何正确理解递归呢?
关键是我们是从分析算法的角度(算法已给出)看还是从设计算法的角度看,从分析算法的角度看是比较难看懂的,可以从设计算法的角度看,这里就涉及到分治算法了,分治算法的最大特点是可以将问题划分成k个相同的问题进行求解,因为是相同的所以等于是执行了k个相同的操作,和递归算法紧紧结合到一起了。
下面是使用分治的思想和递归算法实现的二分法查找:
/**
* 二分法查找:需要预先排序,算法复杂度为:O(logN)
* 根据left和right计算center,将Q(center)和value比较,相等则找到解
* 如果不相等,Q(center) > value确定下区域,Q(center) < value确定上区域
* 下一次重复执行以上操作
* */
int binary(const int array[], int left, int right, int value){
if(left == right){
if(array[left] != value)
return -1;
}
int center = (left + right) / 2;
if(array[center] > value)
return binary(array, left, center - 1, value);
else if(array[center] < value)
return binary(array, center - 1, right, value);
else
return center;
}
int binary_search(const int array[], int len, int value){
return binary(array, 0, len - 1, value);
}
int compare(const void* ap, const void *bp){
int *pa = (int*)ap;
int *pb = (int*)bp;
if(*pa > *pb)
return 1;
else if(*pa < *pb)
return -1;
else
return 0;
}
void basic_print_02(void){
int arrays[SIZE] = {2, 3, -9, 8, -3, 7, 6, -10, 5};
qsort(arrays, SIZE, sizeof(int), compare);
for (int i = 0; i < SIZE; ++i) {
printf("%d ", arrays[i]);
}
int index = binary_search(arrays, SIZE, -99);
printf("\nindex: %d\n", index);
}
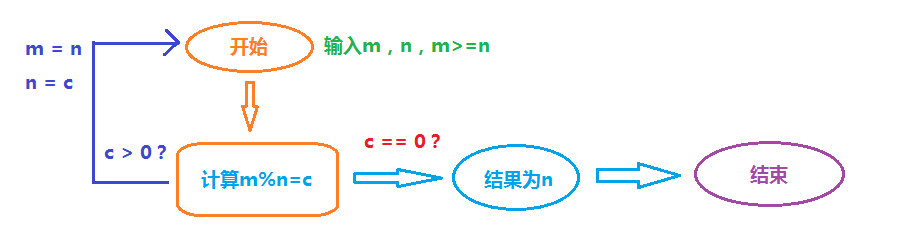
以下同样是使用分治算法和递归算法的例子,还有算法执行的流程图,它的问题是求解两个整数的最大公约数,又称为欧几里德算法:
/**
* 求两个整数的最大公约数,算法复杂度为:O(logN)
* a >= b
* a对b求余等于c1,c1=0确定最大公约数为b
* c1>0,b对c1求余等于c2,c2=0,最大公约数为c1
* c2>0,...(和以上描述相同)
* */
int divisor(int a, int b){
int m = a, n = b;
if(a < b){
m = b;
n = a;
}
int p = m % n;
if(p > 0)
return divisor(n, p);
else
return n;
}
void basic_print_03(void){
int c = divisor(40, 12);
printf("gcd: %d\n", c);
}
3、算法的正确性证明
很多书籍都有提供算法的正确性证明,一般设计完一个算法我们也需要证明该算法执行的正确性,比如我们可能会使用穷举法执行程序验证其正确性,但是这个方法并不是特别靠谱,这里简单叙述一下算法的正确性证明,暂不深入探讨。
算法正确性证明和数学上的证明方法是一样的,首先会有命题或者定理,另外就是证明方法,常提到的有归纳法和反证法。
归纳法先证明基准情形,证明端点处的正确性,例如i>=1,先证明i=1,2的情形,接着进行归纳假设证明,假设i=k成立,证明i=k+1成立。
反证法是先假设命题不成立,试图去证明假设的命题不成立,关于更多的详细内容,后面会进行详细的解释。
以上你可以看到,数据结构和算法是和数学有着莫大的关联的,实际上现在程序设计不需要数学基础也能编程,但是也只能做到使用API的层面上,高级程序设计还是需要数学功底,像人工智能中的机器学习、深度学习等。