接上一节:结构体类型(struct)、联合类型(union)和枚举类型(enum)详解
C语言基本上不会被淘汰,因为C是最接近硬件底层和而且同时适合高级语言开发,在嵌入式开发、单片机、系统开发等,即使在多媒体处理方面,C也是被广泛使用。本章讨论的位操作在嵌入式开发或单片机等这些底层开发中经常用到,而在上层应用开发相对用的少,下面我们先来看一下数的进制问题。
一、二进制、十进制、位和字节
关于数的进制问题,常常觉得多数的资料都讲得很混乱,并没有明确区分数的进制和计算机的存储方式,如果你顺着十进制、二进制、十六进制这样理解,结合补码反码什么的,恐怕会搞得特别混乱。
所以在这里要特别指出两点:数的进制和计算机的存储方式。数的进制可以有很多种,而十进制只是其中一种,而刚好我们最觉得理所当然的一种,数的进制是独立于计算机而存在的,数最自然的表示,例如二进制1010,三进制12102,十进制123等。
计算机的存储方式,数据保存到计算机是需要数字化的,例如对声音振幅的采样简单使用一个十进制表示,对图像色点的采样可以使用三个十进制rgb表示,而计算机只能存储两种值0和1,因此使用二进制表示,所以一个十进制数据存储到计算机中需要转为二进制,但是注意,计算机并不严格直接存储二进制数,例如-1010是二进制数,存储在计算机中变成10110,所以数的进制和计算机的存储方式是不同的。
1、数的进制
(1)N进制数、十进制数和二进制数
N进制数的表示形式为:0 ~ N-1的任意组合,例如五进制数41234,N进制数转为十进制的形式为:X=a0*N^n
+ a1*N^(n-1) + … + an*N^0,五进制数41234转为十进制数为:4*5^4 + 1*5^3 + 2*5^2 + 3*5^1 + 4*5^0。
为什么要转为十进制呢?既然十进制是进制中的其中一种,那么为什么要侧重十进制呢?因为十进制对于我们常人来说最直观,能够直接知道数的意义,所以在这里十进制会是我们侧重的一个,主要是为了观测数字。
十进制数123,可表示为:1 * 10^2 + 2 * 10^1 + 3 * 10^0,10称为基底,N进制的基底为N。同理二进制只有0和1,二进制数1010可表示为1*2^3 + 0*2^2 + 1*2^1 + 0*2^0,利用这种方式可以计算N进制的十进制值。
对于八进制和十六进制,这两种进制仅仅是计算机表示二进制数据的一种相对友好的方式,其中一位八进制使用3位二进制表示,一位十六进制使用4位二进制表示。在这里我们重点研究二进制和十进制,因为计算机使用二进制存储数据,而我们能直观读懂十进制,十六进制的可用数是0到15,其中10-15使用a/A – f/F表示,例如F1A。
(2)二进制数和十进制数的互相转换
数又可分为整数和小数,涉及的转换也要考虑到整数和小数。
二进制转为十进制
二进制整数转为十进制的方法是上面提到的:按位乘2的N次方。二进制小数转换成十进制,首先转换整数部分再转换小数部分,小数部分是按位除以2的N次方,例如:110.11 = 1*2^2
+ 1*2^1 + 0*2^0 + 1/(2^1) + 1/(2^2)。
十进制转为二进制
十进制整数转为二进制:将该整数A除以2,取余数部分,每次除以2的商重新进行下次运算,直到得到的商为0,得到的余数组合则是对应的二进制数,逆序排列,如下图,将十进制整数12转为二进制的过程:

十进制小数转为二进制,若有整数部分先按上面的规则转换成二进制,然后再处理小数部分,小数部分的转换规则是这样:将小数乘以2,取整数部分,每次乘以2的结果都是使用小数部分进行下次运算,重新运算需要排除整数部分,直到小数部分为0,将整数部分顺序排列,得到的结果就是二进制形式的数,下面是将十进制小数5.125转为二进制小数的过程:

2、计算机存储方式
计算机存储数据是使用二进制的方式,所以在这里面向的对象主要是二进制,但是并不是直接按照二进制数的方式存储的,二进制数和计算机二进制存储的不同主要体现在:符号和浮点数,存储的数包括二进制正整数、有符号整数和二进制浮点数。
(1)二进制正整数存储方式
字节是存储系统字符集所需的大小,一般一字节等于8位,该单位也是数据输出速率中使用的单位大小,8位字节又叫做8位组。将一个二进制数0101010从右到左编号,最右边是0,称为低价位,最右边的位是高阶位,计算机存储二进制数一般最左边的1位称为符号位,0表示+正数,1表示-负数。
另外涉及计算机二进制存储的概念是表示的数个数(组合数),以及表示的数范围,举例,一个八位二进制数,能表示的数个数为2^8个,有符号数的范围为-127到128,无符号的数范围为0-255。
而二进制正整数的存储方式是:符号位+数值位,例如0110110是一个二进制正整数,1011001是一个二进制负数,如下代码:
int a = 9;
int b = -9;
printf("%#x\n", a); // 输出:0x9,最高阶位为0,正数
printf("%#x\n", b); // 输出:0xfffffff7,最高阶位为1,负数
二进制的原码由符号位和正数码组成,符号位是0和1,正数码是一个数的绝对值的二进制数,一个二进制数在计算机中存储是以补码方式存储的,所以正整数的补码等于原码。
(2)有符号整数存储方式
表示有符号整数的方式取决于硬件本身,但是一般来说有符号整数在计算机存储也是采用补码的方式存储的,负数或有符号整数的的补码为:符号位不变,其它位按位取反+1,按位取反即0变1,1变0。
举例,-5的二进制数是-101,使用4位存储-5时可表示为1101,符号位不变其它位取反:1010+1为1011,所以这时计算机存储-5为1011。使用int存储-5时,最左边的是符号位1,中间使用0补足,看如下代码:
int a = -5; // 二进制数为-101,int存储为1000 {24个0} 0101
// 二进制存储:数值位取反+1 => 1111 {24个1} 1010 + 1
// = 1111 {24个1} 1011,十六进制为:0xfffffffb
printf("%#x\n", a);
而求原码的方式为:补码数值位-1,取反即可得到原码,求原码主要是为了从计算机的存储数据中得到真正的标示值。
(3)二进制浮点数存储方式
二进制浮点数10101.0101,可使用科学记数法表示为1.01010101*2^100,指数100表示4,又称为阶数,. 01010101称为尾数。按照IEEE 754标准,二进制浮点数的存储由符号位+阶码+尾数组成。
阶码等于阶数+偏移量,阶数是指数,偏移量的计算公式为:2^(e-1)-1,e为阶码的位数,常用的浮点数存储长度为32位和64位,其阶码位数为8位和11位,所以阶码的位数一般是固定的,尾数是科学记数法中的小数部分,如下图:

例如十进制数5.75二进制浮点数101.11,科学记数法表示为1.0111*2^10,符号位为0,阶码等于1111111 + 10等于10000001,尾数为0111,组合成:
0 1000 0001 0111
0000 0000 0000 0000 000,十六进制为40B80000,看如下代码:
float a = 5.75;
printf("%#x\n", *(int *)(&a)); // 输出:0x40b80000
二、二进制按位运算
二进制按位运算又可分为按位逻辑运算和移位运算,按位逻辑运算是将一个或两个二进制数的每一位相应进行逻辑运算,而移位运算是将单个二进制数的每一位进行左移动或右移动。
1、按位逻辑运算
所有按位运算都不会改变原来的值,需要改变原来的值可以使用如+=这样的写法。
(1)按位取反:~
每个二进制位进行取反,1变成0,0变成1,示例代码如下:
// 1、按位取反:~
int number = 12; // 0 000 0000 0000 0000 0000 0000 0000 1100
int result = ~ number; // A = {1 111 1111 1111 1111 1111 1111 1111 0011},A是一个有符号数,需要求出原码得出原数值
printf("%d\n", result); // 原码B = A - 1后,除符号位,其他位按位取反,即原码为:1{0} 1101 = -(2^3 + 2^2 + 2^0)= -13
(2)按位与:&
两个位都为真时为真,否则为假,简写方式为&=,按位与可以用于清除位或关闭位,示例代码如下:
// 2、按位与:&
int a = 3; // 0011
int b = 10; // 1010
int v1 = a & b; // => 0010 = 2
// 简化写法 a &= b => a = a & b
printf("%d\n", v1);
(3)按位或:|
任意一位为真,则为真,否则为假,简写方式为:|=,按位与可用于设置位,示例代码如下:
// 3、按位或:|
int value1 = 7; // 0 00111
int value2 = 17; // 0 10001
int v2 = value1 | value2; // 0 10111 = 16 + 4 + 2 + 1 = 23
// 简化写法 value1 |= value2 => value1 = value1 | value2
printf("%d\n", v2);
(4)按位异或:^
两位有一个为1,结果为1,但不是两个位都是1,简写方式为^=,按位异或可用于切换位,示例代码如下:
// 4、按位异或:^
int p1 = 6; // 00110
int p2 = 16; // 10000
int p3 = p1 ^ p2; // 10110 = 16+4+2 = 22
// 简化写法:p1 ^= p2 => p1 = p1 ^ p2
printf("%d\n", p3);
2、按位逻辑运算的应用
按位运算常用于操作硬件,就是对一个组位的操作,例如一个字节8位组,对一个位或多个位进行某种操作,常规的操作有:打开位、关闭位、切换位和检查位。
(1)掩码(Mask)
按位运算的一个常用的东西就是掩码,一般来说掩码用于屏蔽或清零指定位,掩码主要还是用于设置需要操作的位,例如掩码mask=001010,表明需要操作的位为第1位和第3位,cmd & mask表示cmd除了第1位和第3位保持不变,其它位都关闭(清零),下面详细看一个使用示例:
// 1、掩码(Mask)
int mask1 = 0xf; // 定义掩码,前四位为1
int value1 = 0xfab103;
int result1 = value1 & mask1; // 前四位之后的所有位清零,结果为0x3
int result2 = value1 & ~mask1; // 前四位清零,结果为0xfab100
printf("%#x\n", result1);
printf("%#x\n", result2);
(2)设置位(打开位)
用于设置指定位为1,即打开指定位,同样需要用到掩码mask,使用按位或|,例如mask=1001,cmd | mask表示打开第0位和第3位,其它位保持不变,示例代码如下:
// 2、设置位(打开位)
int mask2 = 0x201; // 指定设置位,分别为:第1位、第10位
int value2 = 0xfb0000;
int result3 = value2 | mask2; // 结果为0xfb0201
printf("%#x\n", result3);
(3)请空位(关闭位)
将指定位清零或关闭,使用逻辑与&,直接关闭某些位需要将掩码进行取反操作,例如需要关闭第1和第3位,掩码可设置为mask=1010,进行逻辑与操作时将掩码进行取反,这样其它位保持不变,第1和第3位会被清零,示例代码如下:
// 3、请空位(关闭位)
int mask3 = 0x1010; // 设置位,分别为:第5位、第13位
int value3 = 0xfb1010;
int result4 = value3 & (~mask3); // 清空第5和第13位,结果为0xfb0000
printf("%#x\n", result4);
(4)切换位
打开已关闭的位,或关闭已打开的位,使用异或^操作,例如掩码mask=100,表示打开或关闭第2位,示例代码如下:
// 4、切换位:打开或关闭指定位
int mask4 = 0x110; // 设置位,分别为:第5位、第9位
int value4 = 0xfb8100;
int result5 = value4 ^ mask4; // 将第5位打开,将第9位关闭,结果为0xfb8010
printf("%#x\n", result5);
(5)检查位
检查或比较指定位的值是否为0或1,那么不比较的位就需要先进行清零,然后再进行比较,例如掩码mask=100,比较第2位是否等于1,可以将掩码与原数进行逻辑与&操作,清除除了第2位的其它位,再与mask进行比较,即(cmd &mask) == mask,示例代码如下:
// 5、检查位:检查指定位的值是否等于0或1,先用掩码清除不必要的位,再比较
int mask5 = 0x1010; // 设置位:检查第5位、第13位是否为1
int value5 = 0xfb1810;
int result6 = (value5 & mask5) == mask5;
printf("%d\n", result6); // 输出:1
3、移位运算
移位运算同样不会改变原来的值,可使用<<=的方式改变原值,对于有符号数的移位处理取决于系统,无符号数空位填充0。
(1)左移运算:<<
所有位按顺序向左边移动,超过左边界的丢弃,右边空位填充0,左移的数学解释为:乘以2的n次幂,n为移动数,示例代码如下:
// 1、左移:<<
int value1 = 0x80ffabcd;
value1 <<= 8; // 简写方式<=,等价于value1 = value1 << 8,结果为0xffabcd00
(2)右移:>>
超出右边界的值丢弃,左边补0,数学解释为:除以2的n次幂,n为移动数,示例代码如下:
// 2、右移:>>
unsigned int value2 = 0x80ffabcd;
value2 >>= 24;// 简写方式>>=,等价于value2 = value2 >> 24,结果为0x00000080
printf("%#x\n", value2);
(3)移位运算的应用
下面给出两个移位运算的应用,第一个为提取位,使用移位+位关闭操作,另一个是输出数值的二进制位,代码如下:
// 3、提取位,提取argb颜色值
int color = 0xffab801a;
int mask = 0xff;
int alpha = (color >> 24) & mask;
int red = (color >> 16) & mask;
int green = (color >> 8) & mask;
int blue = color & mask;
printf("%#x\n", alpha);
printf("%#x\n", red);
printf("%#x\n", green);
printf("%#x\n", blue);
// 4、按二进制格式化输出
int value = 40;
print_bin(value, sizeof(int) * 8);
// 0101 0110
void print_bin(int value, int length){
int status = 0; // 去除前面的空位0
for (int i = length - 1; i >= 0; --i) {
int bin = (value >> i) & 1;
// if(bin == 1)
// status = 1;
// if(status == 1)
printf("%d", bin);
}
}
三、位字段(位变量)和字节对齐
位字段使用一个结构体进行声明,可以提供一种更方便的记录/状态设置,在位层面存储变量数据,存储在signed int或unsigned int中变量中的一组相邻位,,也就是说该结构体变量的成员是按照位的方式进行存储的,存储单元默认为4字节32位,一个存储单元可以存储多个值。
使用结构体声明位字段的要求:就结构体成员分别指定宽度,不指定位宽使用数据成员的默认位宽,不同位宽的变量需要赋值适当的值,不可超过可容纳范围,超过一个int空间的时候,默认进行使用下一个int空间,与上一个int之间留下一个间隙,使用匿名字段,指定位宽为0,可以迫使下一个字段使用下一个int空间,示例代码如下:
union op{
unsigned int bit;
struct p{
unsigned int a : 4;
unsigned int b : 8;
unsigned int c : 20;
} p;
};
void print_12_05(void){
printf("%u\n", sizeof(struct u)); // => 8
// 位字段和按位运算,使用一个int成员和结构体成员
union op op;
op.p.a = 7;
op.p.b = 19;
op.p.c = 30;
unsigned int bit = op.bit;
unsigned int a = bit & 0xf;
unsigned int b = (bit >> 4) & 0xff;
unsigned int c = (bit >> 12) & 0xfffff;
printf("a: %u\n", a);
printf("b: %u\n", b);
printf("c: %u\n", c);
}
其中联合体op的数据字节结构为:
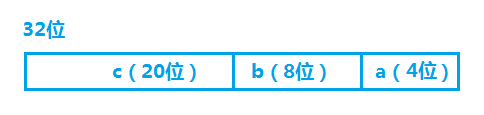
字节对齐
C11提供字节对齐的特性,字节对齐用于描述数据对象在内存中的排列位置,按照不同的字节数对齐对CPU处理数据的速度有所影响,C11提供以下对齐特性:
_Alignof运算符,计算数据类型的对齐要求,对齐字节数大小,返回值类型为size_t。
_Alignas对齐说明符,指定一个变量或类型的对齐值,不能小于基本对齐值,一般在变量声明前添加该说明,clang3.2要求_Alignas在类型说明符后面。
aligned_alloc对齐内存分配,第一个参数为对齐的字节大小,第二个参数为所需字节数大小,下面是一些代码示例:
_Alignas(int) char username;
_Alignas(8) int age;
printf("%u\n", _Alignof(double));
printf("%u\n", _Alignof(username));
printf("%u\n", _Alignof(age));