一、简单k-近邻算法
本文将从k-近邻(kNN)算法的思想开始讲起,使用python3一步一步编写代码进行实战训练。并且,我也提供了相应的数据集,对代码进行了详细的注释。除此之外,本文也对sklearn实现k-近邻算法的方法进行了讲解。实战实例:电影类别分类、约会网站配对效果判定、手写数字识别。
本文出现的所有代码和数据集,均可在我的github上下载,欢迎Follow、Star:Github代码地址
我为大家准备了超详细的学习资料,算法工程师的学习路线和Leetcode刷题笔记,这也是我的自学资料,希望可以帮助读者少走弯路:
1、k-近邻法简介
k近邻法(k-nearest neighbor, k-NN)是1967年由Cover T和Hart P提出的一种基本分类与回归方法。它的工作原理是:存在一个样本数据集合,也称作为训练样本集,并且样本集中每个数据都存在标签,即我们知道样本集中每一个数据与所属分类的对应关系。输入没有标签的新数据后,将新的数据的每个特征与样本集中数据对应的特征进行比较,然后算法提取样本最相似数据(最近邻)的分类标签。一般来说,我们只选择样本数据集中前k个最相似的数据,这就是k-近邻算法中k的出处,通常k是不大于20的整数。最后,选择k个最相似数据中出现次数最多的分类,作为新数据的分类。
举个简单的例子,我们可以使用k-近邻算法分类一个电影是爱情片还是动作片。
表1.1 就是我们已有的数据集合,也就是训练样本集。这个数据集有两个特征,即打斗镜头数和接吻镜头数。除此之外,我们也知道每个电影的所属类型,即分类标签。用肉眼粗略地观察,接吻镜头多的,是爱情片。打斗镜头多的,是动作片。以我们多年的看片经验,这个分类还算合理。如果现在给我一部电影,你告诉我这个电影打斗镜头数和接吻镜头数。不告诉我这个电影类型,我可以根据你给我的信息进行判断,这个电影是属于爱情片还是动作片。而k-近邻算法也可以像我们人一样做到这一点,不同的地方在于,我们的经验更”牛逼”,而k-近邻算法是靠已有的数据。比如,你告诉我这个电影打斗镜头数为2,接吻镜头数为102,我的经验会告诉你这个是爱情片,k-近邻算法也会告诉你这个是爱情片。你又告诉我另一个电影打斗镜头数为49,接吻镜头数为51,我”邪恶”的经验可能会告诉你,这有可能是个”爱情动作片”,画面太美,我不敢想象。 (如果说,你不知道”爱情动作片”是什么?请评论留言与我联系,我需要你这样像我一样纯洁的朋友。) 但是k-近邻算法不会告诉你这些,因为在它的眼里,电影类型只有爱情片和动作片,它会提取样本集中特征最相似数据(最邻近)的分类标签,得到的结果可能是爱情片,也可能是动作片,但绝不会是”爱情动作片”。当然,这些取决于数据集的大小以及最近邻的判断标准等因素。
2、距离度量
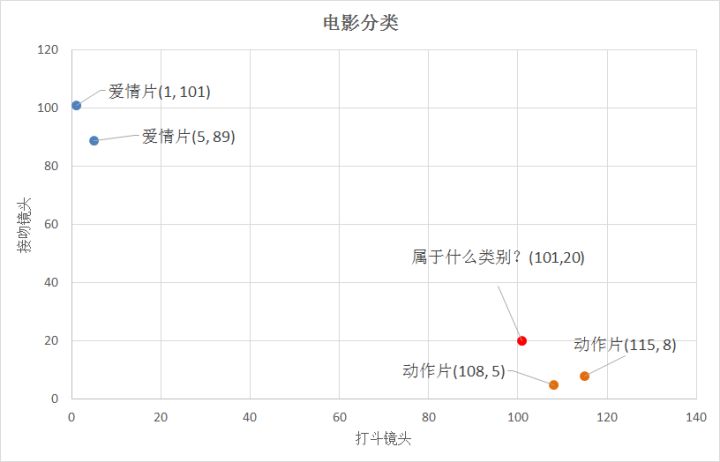
我们已经知道k-近邻算法根据特征比较,然后提取样本集中特征最相似数据(最邻近)的分类标签。那么,如何进行比较呢?比如,我们还是以表1.1为例,怎么判断红色圆点标记的电影所属的类别呢? 如下图所示。
我们可以从散点图大致推断,这个红色圆点标记的电影可能属于动作片,因为距离已知的那两个动作片的圆点更近。k-近邻算法用什么方法进行判断呢?没错,就是距离度量。这个电影分类的例子有2个特征,也就是在2维实数向量空间,可以使用我们高中学过的两点距离公式计算距离,如图1.2所示。
通过计算,我们可以得到如下结果:
- (101,20)->动作片(108,5)的距离约为16.55
- (101,20)->动作片(115,8)的距离约为18.44
- (101,20)->爱情片(5,89)的距离约为118.22
- (101,20)->爱情片(1,101)的距离约为128.69
通过计算可知,红色圆点标记的电影到动作片 (108,5)的距离最近,为16.55。如果算法直接根据这个结果,判断该红色圆点标记的电影为动作片,这个算法就是最近邻算法,而非k-近邻算法。那么k-近邻算法是什么呢?k-近邻算法步骤如下:
- 计算已知类别数据集中的点与当前点之间的距离;
- 按照距离递增次序排序;
- 选取与当前点距离最小的k个点;
- 确定前k个点所在类别的出现频率;
- 返回前k个点所出现频率最高的类别作为当前点的预测分类。
比如,现在我这个k值取3,那么在电影例子中,按距离依次排序的三个点分别是动作片(108,5)、动作片(115,8)、爱情片(5,89)。在这三个点中,动作片出现的频率为三分之二,爱情片出现的频率为三分之一,所以该红色圆点标记的电影为动作片。这个判别过程就是k-近邻算法。
3、Python3代码实现
我们已经知道了k-近邻算法的原理,那么接下来就是使用Python3实现该算法,依然以电影分类为例。
(1)准备数据集
对于表1.1中的数据,我们可以使用numpy直接创建,代码如下:
# -*- coding: UTF-8 -*-
import numpy as np
"""
函数说明:创建数据集
Parameters:
无
Returns:
group - 数据集
labels - 分类标签
Modify:
2017-07-13
"""
def createDataSet():
#四组二维特征
group = np.array([[1,101],[5,89],[108,5],[115,8]])
#四组特征的标签
labels = ['爱情片','爱情片','动作片','动作片']
return group, labels
if __name__ == '__main__':
#创建数据集
group, labels = createDataSet()
#打印数据集
print(group)
print(labels)
运行结果,如图1.3所示:
(2)k-近邻算法
根据两点距离公式,计算距离,选择距离最小的前k个点,并返回分类结果。
# -*- coding: UTF-8 -*-
import numpy as np
import operator
"""
函数说明:创建数据集
Parameters:
无
Returns:
group - 数据集
labels - 分类标签
Modify:
2017-07-13
"""
def createDataSet():
#四组二维特征
group = np.array([[1,101],[5,89],[108,5],[115,8]])
#四组特征的标签
labels = ['爱情片','爱情片','动作片','动作片']
return group, labels
"""
函数说明:kNN算法,分类器
Parameters:
inX - 用于分类的数据(测试集)
dataSet - 用于训练的数据(训练集)
labes - 分类标签
k - kNN算法参数,选择距离最小的k个点
Returns:
sortedClassCount[0][0] - 分类结果
Modify:
2017-07-13
"""
def classify0(inX, dataSet, labels, k):
#numpy函数shape[0]返回dataSet的行数
dataSetSize = dataSet.shape[0]
#在列向量方向上重复inX共1次(横向),行向量方向上重复inX共dataSetSize次(纵向)
diffMat = np.tile(inX, (dataSetSize, 1)) - dataSet
#二维特征相减后平方
sqDiffMat = diffMat**2
#sum()所有元素相加,sum(0)列相加,sum(1)行相加
sqDistances = sqDiffMat.sum(axis=1)
#开方,计算出距离
distances = sqDistances**0.5
#返回distances中元素从小到大排序后的索引值
sortedDistIndices = distances.argsort()
#定一个记录类别次数的字典
classCount = {}
for i in range(k):
#取出前k个元素的类别
voteIlabel = labels[sortedDistIndices[i]]
#dict.get(key,default=None),字典的get()方法,返回指定键的值,如果值不在字典中返回默认值。
#计算类别次数
classCount[voteIlabel] = classCount.get(voteIlabel,0) + 1
#python3中用items()替换python2中的iteritems()
#key=operator.itemgetter(1)根据字典的值进行排序
#key=operator.itemgetter(0)根据字典的键进行排序
#reverse降序排序字典
sortedClassCount = sorted(classCount.items(),key=operator.itemgetter(1),reverse=True)
#返回次数最多的类别,即所要分类的类别
return sortedClassCount[0][0]
if __name__ == '__main__':
#创建数据集
group, labels = createDataSet()
#测试集
test = [101,20]
#kNN分类
test_class = classify0(test, group, labels, 3)
#打印分类结果
print(test_class)
运行结果,如图1.4所示:
可以看到,分类结果根据我们的”经验”,是正确的,尽管这种分类比较耗时,用时1.4s。
到这里,也许有人早已经发现,电影例子中的特征是2维的,这样的距离度量可以用两 点距离公式计算,但是如果是更高维的呢?对,没错。我们可以用欧氏距离(也称欧几里德度量),如图1.5所示。我们高中所学的两点距离公式就是欧氏距离在二维空间上的公式,也就是欧氏距离的n的值为2的情况。
看到这里,有人可能会问:“分类器何种情况下会出错?”或者“答案是否总是正确的?”答案是否定的,分类器并不会得到百分百正确的结果,我们可以使用多种方法检测分类器的正确率。此外分类器的性能也会受到多种因素的影响,如分类器设置和数据集等。不同的算法在不同数据集上的表现可能完全不同。为了测试分类器的效果,我们可以使用已知答案的数据,当然答案不能告诉分类器,检验分类器给出的结果是否符合预期结果。通过大量的测试数据,我们可以得到分类器的错误率-分类器给出错误结果的次数除以测试执行的总数。错误率是常用的评估方法,主要用于评估分类器在某个数据集上的执行效果。完美分类器的错误率为0,最差分类器的错误率是1.0。同时,我们也不难发现,k-近邻算法没有进行数据的训练,直接使用未知的数据与已知的数据进行比较,得到结果。因此,可以说k-近邻算法不具有显式的学习过程。
二、k-近邻算法实战之约会网站配对效果判定
上一小结学习了简单的k-近邻算法的实现方法,但是这并不是完整的k-近邻算法流程,k-近邻算法的一般流程:
- 收集数据:可以使用爬虫进行数据的收集,也可以使用第三方提供的免费或收费的数据。一般来讲,数据放在txt文本文件中,按照一定的格式进行存储,便于解析及处理。
- 准备数据:使用Python解析、预处理数据。
- 分析数据:可以使用很多方法对数据进行分析,例如使用Matplotlib将数据可视化。
- 测试算法:计算错误率。
- 使用算法:错误率在可接受范围内,就可以运行k-近邻算法进行分类。
已经了解了k-近邻算法的一般流程,下面开始进入实战内容。
1、实战背景
海伦女士一直使用在线约会网站寻找适合自己的约会对象。尽管约会网站会推荐不同的任选,但她并不是喜欢每一个人。经过一番总结,她发现自己交往过的人可以进行如下分类:
- 不喜欢的人
- 魅力一般的人
- 极具魅力的人
海伦收集约会数据已经有了一段时间,她把这些数据存放在文本文件datingTestSet.txt中,每个样本数据占据一行,总共有1000行。datingTestSet.txt数据下载: 数据集下载
海伦收集的样本数据主要包含以下3种特征:
- 每年获得的飞行常客里程数
- 玩视频游戏所消耗时间百分比
- 每周消费的冰淇淋公升数
这里不得不吐槽一句,海伦是个小吃货啊,冰淇淋公斤数都影响自己择偶标准。打开txt文本文件,数据格式如图2.1所示。
2、准备数据:数据解析
在将上述特征数据输入到分类器前,必须将待处理的数据的格式改变为分类器可以接收的格式。分类器接收的数据是什么格式的?从上小结已经知道,要将数据分类两部分,即特征矩阵和对应的分类标签向量。在kNN_test02.py文件中创建名为file2matrix的函数,以此来处理输入格式问题。 将datingTestSet.txt放到与kNN_test02.py相同目录下,编写代码如下:
# -*- coding: UTF-8 -*-
import numpy as np
"""
函数说明:打开并解析文件,对数据进行分类:1代表不喜欢,2代表魅力一般,3代表极具魅力
Parameters:
filename - 文件名
Returns:
returnMat - 特征矩阵
classLabelVector - 分类Label向量
Modify:
2017-03-24
"""
def file2matrix(filename):
#打开文件
fr = open(filename)
#读取文件所有内容
arrayOLines = fr.readlines()
#得到文件行数
numberOfLines = len(arrayOLines)
#返回的NumPy矩阵,解析完成的数据:numberOfLines行,3列
returnMat = np.zeros((numberOfLines,3))
#返回的分类标签向量
classLabelVector = []
#行的索引值
index = 0
for line in arrayOLines:
#s.strip(rm),当rm空时,默认删除空白符(包括'\n','\r','\t',' ')
line = line.strip()
#使用s.split(str="",num=string,cout(str))将字符串根据'\t'分隔符进行切片。
listFromLine = line.split('\t')
#将数据前三列提取出来,存放到returnMat的NumPy矩阵中,也就是特征矩阵
returnMat[index,:] = listFromLine[0:3]
#根据文本中标记的喜欢的程度进行分类,1代表不喜欢,2代表魅力一般,3代表极具魅力
if listFromLine[-1] == 'didntLike':
classLabelVector.append(1)
elif listFromLine[-1] == 'smallDoses':
classLabelVector.append(2)
elif listFromLine[-1] == 'largeDoses':
classLabelVector.append(3)
index += 1
return returnMat, classLabelVector
"""
函数说明:main函数
Parameters:
无
Returns:
无
Modify:
2017-03-24
"""
if __name__ == '__main__':
#打开的文件名
filename = "datingTestSet.txt"
#打开并处理数据
datingDataMat, datingLabels = file2matrix(filename)
print(datingDataMat)
print(datingLabels)
运行上述代码,得到的数据解析结果如图2.2所示。
可以看到,我们已经顺利导入数据,并对数据进行解析,格式化为分类器需要的数据格式。接着我们需要了解数据的真正含义。可以通过友好、直观的图形化的方式观察数据。
3、分析数据:数据可视化
在kNN_test02.py文件中编写名为showdatas的函数,用来将数据可视化。编写代码如下:
# -*- coding: UTF-8 -*-
from matplotlib.font_manager import FontProperties
import matplotlib.lines as mlines
import matplotlib.pyplot as plt
import numpy as np
"""
函数说明:打开并解析文件,对数据进行分类:1代表不喜欢,2代表魅力一般,3代表极具魅力
Parameters:
filename - 文件名
Returns:
returnMat - 特征矩阵
classLabelVector - 分类Label向量
Modify:
2017-03-24
"""
def file2matrix(filename):
#打开文件
fr = open(filename)
#读取文件所有内容
arrayOLines = fr.readlines()
#得到文件行数
numberOfLines = len(arrayOLines)
#返回的NumPy矩阵,解析完成的数据:numberOfLines行,3列
returnMat = np.zeros((numberOfLines,3))
#返回的分类标签向量
classLabelVector = []
#行的索引值
index = 0
for line in arrayOLines:
#s.strip(rm),当rm空时,默认删除空白符(包括'\n','\r','\t',' ')
line = line.strip()
#使用s.split(str="",num=string,cout(str))将字符串根据'\t'分隔符进行切片。
listFromLine = line.split('\t')
#将数据前三列提取出来,存放到returnMat的NumPy矩阵中,也就是特征矩阵
returnMat[index,:] = listFromLine[0:3]
#根据文本中标记的喜欢的程度进行分类,1代表不喜欢,2代表魅力一般,3代表极具魅力
if listFromLine[-1] == 'didntLike':
classLabelVector.append(1)
elif listFromLine[-1] == 'smallDoses':
classLabelVector.append(2)
elif listFromLine[-1] == 'largeDoses':
classLabelVector.append(3)
index += 1
return returnMat, classLabelVector
"""
函数说明:可视化数据
Parameters:
datingDataMat - 特征矩阵
datingLabels - 分类Label
Returns:
无
Modify:
2017-03-24
"""
def showdatas(datingDataMat, datingLabels):
#设置汉字格式
font = FontProperties(fname=r"c:\windows\fonts\simsun.ttc", size=14)
#将fig画布分隔成1行1列,不共享x轴和y轴,fig画布的大小为(13,8)
#当nrow=2,nclos=2时,代表fig画布被分为四个区域,axs[0][0]表示第一行第一个区域
fig, axs = plt.subplots(nrows=2, ncols=2,sharex=False, sharey=False, figsize=(13,8))
numberOfLabels = len(datingLabels)
LabelsColors = []
for i in datingLabels:
if i == 1:
LabelsColors.append('black')
if i == 2:
LabelsColors.append('orange')
if i == 3:
LabelsColors.append('red')
#画出散点图,以datingDataMat矩阵的第一(飞行常客例程)、第二列(玩游戏)数据画散点数据,散点大小为15,透明度为0.5
axs[0][0].scatter(x=datingDataMat[:,0], y=datingDataMat[:,1], color=LabelsColors,s=15, alpha=.5)
#设置标题,x轴label,y轴label
axs0_title_text = axs[0][0].set_title(u'每年获得的飞行常客里程数与玩视频游戏所消耗时间占比',FontProperties=font)
axs0_xlabel_text = axs[0][0].set_xlabel(u'每年获得的飞行常客里程数',FontProperties=font)
axs0_ylabel_text = axs[0][0].set_ylabel(u'玩视频游戏所消耗时间占',FontProperties=font)
plt.setp(axs0_title_text, size=9, weight='bold', color='red')
plt.setp(axs0_xlabel_text, size=7, weight='bold', color='black')
plt.setp(axs0_ylabel_text, size=7, weight='bold', color='black')
#画出散点图,以datingDataMat矩阵的第一(飞行常客例程)、第三列(冰激凌)数据画散点数据,散点大小为15,透明度为0.5
axs[0][1].scatter(x=datingDataMat[:,0], y=datingDataMat[:,2], color=LabelsColors,s=15, alpha=.5)
#设置标题,x轴label,y轴label
axs1_title_text = axs[0][1].set_title(u'每年获得的飞行常客里程数与每周消费的冰激淋公升数',FontProperties=font)
axs1_xlabel_text = axs[0][1].set_xlabel(u'每年获得的飞行常客里程数',FontProperties=font)
axs1_ylabel_text = axs[0][1].set_ylabel(u'每周消费的冰激淋公升数',FontProperties=font)
plt.setp(axs1_title_text, size=9, weight='bold', color='red')
plt.setp(axs1_xlabel_text, size=7, weight='bold', color='black')
plt.setp(axs1_ylabel_text, size=7, weight='bold', color='black')
#画出散点图,以datingDataMat矩阵的第二(玩游戏)、第三列(冰激凌)数据画散点数据,散点大小为15,透明度为0.5
axs[1][0].scatter(x=datingDataMat[:,1], y=datingDataMat[:,2], color=LabelsColors,s=15, alpha=.5)
#设置标题,x轴label,y轴label
axs2_title_text = axs[1][0].set_title(u'玩视频游戏所消耗时间占比与每周消费的冰激淋公升数',FontProperties=font)
axs2_xlabel_text = axs[1][0].set_xlabel(u'玩视频游戏所消耗时间占比',FontProperties=font)
axs2_ylabel_text = axs[1][0].set_ylabel(u'每周消费的冰激淋公升数',FontProperties=font)
plt.setp(axs2_title_text, size=9, weight='bold', color='red')
plt.setp(axs2_xlabel_text, size=7, weight='bold', color='black')
plt.setp(axs2_ylabel_text, size=7, weight='bold', color='black')
#设置图例
didntLike = mlines.Line2D([], [], color='black', marker='.',
markersize=6, label='didntLike')
smallDoses = mlines.Line2D([], [], color='orange', marker='.',
markersize=6, label='smallDoses')
largeDoses = mlines.Line2D([], [], color='red', marker='.',
markersize=6, label='largeDoses')
#添加图例
axs[0][0].legend(handles=[didntLike,smallDoses,largeDoses])
axs[0][1].legend(handles=[didntLike,smallDoses,largeDoses])
axs[1][0].legend(handles=[didntLike,smallDoses,largeDoses])
#显示图片
plt.show()
"""
函数说明:main函数
Parameters:
无
Returns:
无
Modify:
2017-03-24
"""
if __name__ == '__main__':
#打开的文件名
filename = "datingTestSet.txt"
#打开并处理数据
datingDataMat, datingLabels = file2matrix(filename)
showdatas(datingDataMat, datingLabels)
运行上述代码,可以看到可视化结果如图2.3所示。
通过数据可以很直观的发现数据的规律,比如以玩游戏所消耗时间占比与每年获得的飞行常客里程数,只考虑这二维的特征信息,给我的感觉就是海伦喜欢有生活质量的男人。为什么这么说呢?每年获得的飞行常客里程数表明,海伦喜欢能享受飞行常客奖励计划的男人,但是不能经常坐飞机,疲于奔波,满世界飞。同时,这个男人也要玩视频游戏,并且占一定时间比例。能到处飞,又能经常玩游戏的男人是什么样的男人?很显然,有生活质量,并且生活悠闲的人。我的分析,仅仅是通过可视化的数据总结的个人看法。我想,每个人的感受应该也是不尽相同。
4、准备数据:数据归一化
表2.1给出了四组样本,如果想要计算样本3和样本4之间的距离,可以使用欧式距离公式计算。
计算方法如图2.4所示。
我们很容易发现,上面方程中数字差值最大的属性对计算结果的影响最大,也就是说,每年获取的飞行常客里程数对于计算结果的影响将远远大于表2.1中其他两个特征-玩视频游戏所耗时间占比和每周消费冰淇淋公斤数的影响。而产生这种现象的唯一原因,仅仅是因为飞行常客里程数远大于其他特征值。但海伦认为这三种特征是同等重要的,因此作为三个等权重的特征之一,飞行常客里程数并不应该如此严重地影响到计算结果。
在处理这种不同取值范围的特征值时,我们通常采用的方法是将数值归一化,如将取值范围处理为0到1或者-1到1之间。下面的公式可以将任意取值范围的特征值转化为0到1区间内的值:
newValue = (oldValue – min) / (max – min)
其中min和max分别是数据集中的最小特征值和最大特征值。虽然改变数值取值范围增加了分类器的复杂度,但为了得到准确结果,我们必须这样做。在kNN_test02.py文件中编写名为autoNorm的函数,用该函数自动将数据归一化。代码如下:
# -*- coding: UTF-8 -*-
import numpy as np
"""
函数说明:打开并解析文件,对数据进行分类:1代表不喜欢,2代表魅力一般,3代表极具魅力
Parameters:
filename - 文件名
Returns:
returnMat - 特征矩阵
classLabelVector - 分类Label向量
Modify:
2017-03-24
"""
def file2matrix(filename):
#打开文件
fr = open(filename)
#读取文件所有内容
arrayOLines = fr.readlines()
#得到文件行数
numberOfLines = len(arrayOLines)
#返回的NumPy矩阵,解析完成的数据:numberOfLines行,3列
returnMat = np.zeros((numberOfLines,3))
#返回的分类标签向量
classLabelVector = []
#行的索引值
index = 0
for line in arrayOLines:
#s.strip(rm),当rm空时,默认删除空白符(包括'\n','\r','\t',' ')
line = line.strip()
#使用s.split(str="",num=string,cout(str))将字符串根据'\t'分隔符进行切片。
listFromLine = line.split('\t')
#将数据前三列提取出来,存放到returnMat的NumPy矩阵中,也就是特征矩阵
returnMat[index,:] = listFromLine[0:3]
#根据文本中标记的喜欢的程度进行分类,1代表不喜欢,2代表魅力一般,3代表极具魅力
if listFromLine[-1] == 'didntLike':
classLabelVector.append(1)
elif listFromLine[-1] == 'smallDoses':
classLabelVector.append(2)
elif listFromLine[-1] == 'largeDoses':
classLabelVector.append(3)
index += 1
return returnMat, classLabelVector
"""
函数说明:对数据进行归一化
Parameters:
dataSet - 特征矩阵
Returns:
normDataSet - 归一化后的特征矩阵
ranges - 数据范围
minVals - 数据最小值
Modify:
2017-03-24
"""
def autoNorm(dataSet):
#获得数据的最小值
minVals = dataSet.min(0)
maxVals = dataSet.max(0)
#最大值和最小值的范围
ranges = maxVals - minVals
#shape(dataSet)返回dataSet的矩阵行列数
normDataSet = np.zeros(np.shape(dataSet))
#返回dataSet的行数
m = dataSet.shape[0]
#原始值减去最小值
normDataSet = dataSet - np.tile(minVals, (m, 1))
#除以最大和最小值的差,得到归一化数据
normDataSet = normDataSet / np.tile(ranges, (m, 1))
#返回归一化数据结果,数据范围,最小值
return normDataSet, ranges, minVals
"""
函数说明:main函数
Parameters:
无
Returns:
无
Modify:
2017-03-24
"""
if __name__ == '__main__':
#打开的文件名
filename = "datingTestSet.txt"
#打开并处理数据
datingDataMat, datingLabels = file2matrix(filename)
normDataSet, ranges, minVals = autoNorm(datingDataMat)
print(normDataSet)
print(ranges)
print(minVals)
运行上述代码,得到结果如图2.4所示。
从图2.4的运行结果可以看到,我们已经顺利将数据归一化了,并且求出了数据的取值范围和数据的最小值,这两个值是在分类的时候需要用到的,直接先求解出来,也算是对数据预处理了。
5、测试算法:验证分类器
机器学习算法一个很重要的工作就是评估算法的正确率,通常我们只提供已有数据的90%作为训练样本来训练分类器,而使用其余的10%数据去测试分类器,检测分类器的正确率。需要注意的是,10%的测试数据应该是随机选择的,由于海伦提供的数据并没有按照特定目的来排序,所以我们可以随意选择10%数据而不影响其随机性。
为了测试分类器效果,在kNN_test02.py文件中创建函数datingClassTest,编写代码如下:
# -*- coding: UTF-8 -*-
import numpy as np
import operator
"""
函数说明:kNN算法,分类器
Parameters:
inX - 用于分类的数据(测试集)
dataSet - 用于训练的数据(训练集)
labes - 分类标签
k - kNN算法参数,选择距离最小的k个点
Returns:
sortedClassCount[0][0] - 分类结果
Modify:
2017-03-24
"""
def classify0(inX, dataSet, labels, k):
#numpy函数shape[0]返回dataSet的行数
dataSetSize = dataSet.shape[0]
#在列向量方向上重复inX共1次(横向),行向量方向上重复inX共dataSetSize次(纵向)
diffMat = np.tile(inX, (dataSetSize, 1)) - dataSet
#二维特征相减后平方
sqDiffMat = diffMat**2
#sum()所有元素相加,sum(0)列相加,sum(1)行相加
sqDistances = sqDiffMat.sum(axis=1)
#开方,计算出距离
distances = sqDistances**0.5
#返回distances中元素从小到大排序后的索引值
sortedDistIndices = distances.argsort()
#定一个记录类别次数的字典
classCount = {}
for i in range(k):
#取出前k个元素的类别
voteIlabel = labels[sortedDistIndices[i]]
#dict.get(key,default=None),字典的get()方法,返回指定键的值,如果值不在字典中返回默认值。
#计算类别次数
classCount[voteIlabel] = classCount.get(voteIlabel,0) + 1
#python3中用items()替换python2中的iteritems()
#key=operator.itemgetter(1)根据字典的值进行排序
#key=operator.itemgetter(0)根据字典的键进行排序
#reverse降序排序字典
sortedClassCount = sorted(classCount.items(),key=operator.itemgetter(1),reverse=True)
#返回次数最多的类别,即所要分类的类别
return sortedClassCount[0][0]
"""
函数说明:打开并解析文件,对数据进行分类:1代表不喜欢,2代表魅力一般,3代表极具魅力
Parameters:
filename - 文件名
Returns:
returnMat - 特征矩阵
classLabelVector - 分类Label向量
Modify:
2017-03-24
"""
def file2matrix(filename):
#打开文件
fr = open(filename)
#读取文件所有内容
arrayOLines = fr.readlines()
#得到文件行数
numberOfLines = len(arrayOLines)
#返回的NumPy矩阵,解析完成的数据:numberOfLines行,3列
returnMat = np.zeros((numberOfLines,3))
#返回的分类标签向量
classLabelVector = []
#行的索引值
index = 0
for line in arrayOLines:
#s.strip(rm),当rm空时,默认删除空白符(包括'\n','\r','\t',' ')
line = line.strip()
#使用s.split(str="",num=string,cout(str))将字符串根据'\t'分隔符进行切片。
listFromLine = line.split('\t')
#将数据前三列提取出来,存放到returnMat的NumPy矩阵中,也就是特征矩阵
returnMat[index,:] = listFromLine[0:3]
#根据文本中标记的喜欢的程度进行分类,1代表不喜欢,2代表魅力一般,3代表极具魅力
if listFromLine[-1] == 'didntLike':
classLabelVector.append(1)
elif listFromLine[-1] == 'smallDoses':
classLabelVector.append(2)
elif listFromLine[-1] == 'largeDoses':
classLabelVector.append(3)
index += 1
return returnMat, classLabelVector
"""
函数说明:对数据进行归一化
Parameters:
dataSet - 特征矩阵
Returns:
normDataSet - 归一化后的特征矩阵
ranges - 数据范围
minVals - 数据最小值
Modify:
2017-03-24
"""
def autoNorm(dataSet):
#获得数据的最小值
minVals = dataSet.min(0)
maxVals = dataSet.max(0)
#最大值和最小值的范围
ranges = maxVals - minVals
#shape(dataSet)返回dataSet的矩阵行列数
normDataSet = np.zeros(np.shape(dataSet))
#返回dataSet的行数
m = dataSet.shape[0]
#原始值减去最小值
normDataSet = dataSet - np.tile(minVals, (m, 1))
#除以最大和最小值的差,得到归一化数据
normDataSet = normDataSet / np.tile(ranges, (m, 1))
#返回归一化数据结果,数据范围,最小值
return normDataSet, ranges, minVals
"""
函数说明:分类器测试函数
Parameters:
无
Returns:
normDataSet - 归一化后的特征矩阵
ranges - 数据范围
minVals - 数据最小值
Modify:
2017-03-24
"""
def datingClassTest():
#打开的文件名
filename = "datingTestSet.txt"
#将返回的特征矩阵和分类向量分别存储到datingDataMat和datingLabels中
datingDataMat, datingLabels = file2matrix(filename)
#取所有数据的百分之十
hoRatio = 0.10
#数据归一化,返回归一化后的矩阵,数据范围,数据最小值
normMat, ranges, minVals = autoNorm(datingDataMat)
#获得normMat的行数
m = normMat.shape[0]
#百分之十的测试数据的个数
numTestVecs = int(m * hoRatio)
#分类错误计数
errorCount = 0.0
for i in range(numTestVecs):
#前numTestVecs个数据作为测试集,后m-numTestVecs个数据作为训练集
classifierResult = classify0(normMat[i,:], normMat[numTestVecs:m,:],
datingLabels[numTestVecs:m], 4)
print("分类结果:%d\t真实类别:%d" % (classifierResult, datingLabels[i]))
if classifierResult != datingLabels[i]:
errorCount += 1.0
print("错误率:%f%%" %(errorCount/float(numTestVecs)*100))
"""
函数说明:main函数
Parameters:
无
Returns:
无
Modify:
2017-03-24
"""
if __name__ == '__main__':
datingClassTest()
运行上述代码,得到结果如图2.5所示。
从图2.5验证分类器结果中可以看出,错误率是3%,这是一个想当不错的结果。我们可以改变函数datingClassTest内变量hoRatio和分类器k的值,检测错误率是否随着变量值的变化而增加。依赖于分类算法、数据集和程序设置,分类器的输出结果可能有很大的不同。
6、使用算法:构建完整可用系统
我们可以给海伦一个小段程序,通过该程序海伦会在约会网站上找到某个人并输入他的信息。程序会给出她对男方喜欢程度的预测值。
在kNN_test02.py文件中创建函数classifyPerson,代码如下:
# -*- coding: UTF-8 -*-
import numpy as np
import operator
"""
函数说明:kNN算法,分类器
Parameters:
inX - 用于分类的数据(测试集)
dataSet - 用于训练的数据(训练集)
labes - 分类标签
k - kNN算法参数,选择距离最小的k个点
Returns:
sortedClassCount[0][0] - 分类结果
Modify:
2017-03-24
"""
def classify0(inX, dataSet, labels, k):
#numpy函数shape[0]返回dataSet的行数
dataSetSize = dataSet.shape[0]
#在列向量方向上重复inX共1次(横向),行向量方向上重复inX共dataSetSize次(纵向)
diffMat = np.tile(inX, (dataSetSize, 1)) - dataSet
#二维特征相减后平方
sqDiffMat = diffMat**2
#sum()所有元素相加,sum(0)列相加,sum(1)行相加
sqDistances = sqDiffMat.sum(axis=1)
#开方,计算出距离
distances = sqDistances**0.5
#返回distances中元素从小到大排序后的索引值
sortedDistIndices = distances.argsort()
#定一个记录类别次数的字典
classCount = {}
for i in range(k):
#取出前k个元素的类别
voteIlabel = labels[sortedDistIndices[i]]
#dict.get(key,default=None),字典的get()方法,返回指定键的值,如果值不在字典中返回默认值。
#计算类别次数
classCount[voteIlabel] = classCount.get(voteIlabel,0) + 1
#python3中用items()替换python2中的iteritems()
#key=operator.itemgetter(1)根据字典的值进行排序
#key=operator.itemgetter(0)根据字典的键进行排序
#reverse降序排序字典
sortedClassCount = sorted(classCount.items(),key=operator.itemgetter(1),reverse=True)
#返回次数最多的类别,即所要分类的类别
return sortedClassCount[0][0]
"""
函数说明:打开并解析文件,对数据进行分类:1代表不喜欢,2代表魅力一般,3代表极具魅力
Parameters:
filename - 文件名
Returns:
returnMat - 特征矩阵
classLabelVector - 分类Label向量
Modify:
2017-03-24
"""
def file2matrix(filename):
#打开文件
fr = open(filename)
#读取文件所有内容
arrayOLines = fr.readlines()
#得到文件行数
numberOfLines = len(arrayOLines)
#返回的NumPy矩阵,解析完成的数据:numberOfLines行,3列
returnMat = np.zeros((numberOfLines,3))
#返回的分类标签向量
classLabelVector = []
#行的索引值
index = 0
for line in arrayOLines:
#s.strip(rm),当rm空时,默认删除空白符(包括'\n','\r','\t',' ')
line = line.strip()
#使用s.split(str="",num=string,cout(str))将字符串根据'\t'分隔符进行切片。
listFromLine = line.split('\t')
#将数据前三列提取出来,存放到returnMat的NumPy矩阵中,也就是特征矩阵
returnMat[index,:] = listFromLine[0:3]
#根据文本中标记的喜欢的程度进行分类,1代表不喜欢,2代表魅力一般,3代表极具魅力
if listFromLine[-1] == 'didntLike':
classLabelVector.append(1)
elif listFromLine[-1] == 'smallDoses':
classLabelVector.append(2)
elif listFromLine[-1] == 'largeDoses':
classLabelVector.append(3)
index += 1
return returnMat, classLabelVector
"""
函数说明:对数据进行归一化
Parameters:
dataSet - 特征矩阵
Returns:
normDataSet - 归一化后的特征矩阵
ranges - 数据范围
minVals - 数据最小值
Modify:
2017-03-24
"""
def autoNorm(dataSet):
#获得数据的最小值
minVals = dataSet.min(0)
maxVals = dataSet.max(0)
#最大值和最小值的范围
ranges = maxVals - minVals
#shape(dataSet)返回dataSet的矩阵行列数
normDataSet = np.zeros(np.shape(dataSet))
#返回dataSet的行数
m = dataSet.shape[0]
#原始值减去最小值
normDataSet = dataSet - np.tile(minVals, (m, 1))
#除以最大和最小值的差,得到归一化数据
normDataSet = normDataSet / np.tile(ranges, (m, 1))
#返回归一化数据结果,数据范围,最小值
return normDataSet, ranges, minVals
"""
函数说明:通过输入一个人的三维特征,进行分类输出
Parameters:
无
Returns:
无
Modify:
2017-03-24
"""
def classifyPerson():
#输出结果
resultList = ['讨厌','有些喜欢','非常喜欢']
#三维特征用户输入
precentTats = float(input("玩视频游戏所耗时间百分比:"))
ffMiles = float(input("每年获得的飞行常客里程数:"))
iceCream = float(input("每周消费的冰激淋公升数:"))
#打开的文件名
filename = "datingTestSet.txt"
#打开并处理数据
datingDataMat, datingLabels = file2matrix(filename)
#训练集归一化
normMat, ranges, minVals = autoNorm(datingDataMat)
#生成NumPy数组,测试集
inArr = np.array([ffMiles, precentTats, iceCream])
#测试集归一化
norminArr = (inArr - minVals) / ranges
#返回分类结果
classifierResult = classify0(norminArr, normMat, datingLabels, 3)
#打印结果
print("你可能%s这个人" % (resultList[classifierResult-1]))
"""
函数说明:main函数
Parameters:
无
Returns:
无
Modify:
2017-03-24
"""
if __name__ == '__main__':
classifyPerson()
在cmd中,运行程序,并输入数据(12,44000,0.5),预测结果是”你可能有些喜欢这个人”,也就是这个人魅力一般。一共有三个档次:讨厌、有些喜欢、非常喜欢,对应着不喜欢的人、魅力一般的人、极具魅力的人。结果如图2.6所示。
三、k-近邻算法实战之sklearn手写数字识别
1、实战背景
对于需要识别的数字已经使用图形处理软件,处理成具有相同的色彩和大小:宽高是32像素x32像素。尽管采用本文格式存储图像不能有效地利用内存空间,但是为了方便理解,我们将图片转换为文本格式,数字的文本格式如图3.1所示。
与此同时,这些文本格式存储的数字的文件命名也很有特点,格式为:数字的值_该数字的样本序号,如图3.2所示。
对于这样已经整理好的文本,我们可以直接使用Python处理,进行数字预测。数据集分为训练集和测试集,使用上小结的方法,自己设计k-近邻算法分类器,可以实现分类。数据集和实现代码下载地址:数据集下载
这里不再讲解自己用Python写的k-邻域分类器的方法,因为这不是本小节的重点。接下来,我们将使用强大的第三方Python科学计算库Sklearn构建手写数字系统。
2、sklearn简介
Scikit learn 也简称sklearn,是机器学习领域当中最知名的python模块之一。sklearn包含了很多机器学习的方式:
- Classification 分类
- Regression 回归
- Clustering 非监督分类
- Dimensionality reduction 数据降维
- Model Selection 模型选择
- Preprocessing 数据与处理
使用sklearn可以很方便地让我们实现一个机器学习算法。一个复杂度算法的实现,使用sklearn可能只需要调用几行API即可。所以学习sklearn,可以有效减少我们特定任务的实现周期。
3、sklearn安装
在安装sklearn之前,需要安装两个库,即numpy+mkl和scipy。不要使用pip3直接进行安装,因为pip3默安装的是numpy,而不是numpy+mkl。第三方库下载地址:http://www.lfd.uci.edu/~gohlke/pythonlibs/
这个网站的使用方法,我在之前的文章里有讲过:http://blog.csdn.net/c406495762/article/details/60156205
找到对应python版本的numpy+mkl和scipy,下载安装即可,如图3.3和图3.4所示。
使用pip3安装好这两个whl文件后,使用如下指令安装sklearn。
pip3 install -U scikit-learn
4、sklearn实现k-近邻算法简介
官网英文文档:点我查看
sklearn.neighbors模块实现了k-近邻算法,内容如图3.5所示。
我们使用sklearn.neighbors.KNeighborsClassifier就可以是实现上小结,我们实现的k-近邻算法。KNeighborsClassifier函数一共有8个参数,如图3.6所示。
KNneighborsClassifier参数说明:
- n_neighbors:默认为5,就是k-NN的k的值,选取最近的k个点。
- weights:默认是uniform,参数可以是uniform、distance,也可以是用户自己定义的函数。uniform是均等的权重,就说所有的邻近点的权重都是相等的。distance是不均等的权重,距离近的点比距离远的点的影响大。用户自定义的函数,接收距离的数组,返回一组维数相同的权重。
- algorithm:快速k近邻搜索算法,默认参数为auto,可以理解为算法自己决定合适的搜索算法。除此之外,用户也可以自己指定搜索算法ball_tree、kd_tree、brute方法进行搜索,brute是蛮力搜索,也就是线性扫描,当训练集很大时,计算非常耗时。kd_tree,构造kd树存储数据以便对其进行快速检索的树形数据结构,kd树也就是数据结构中的二叉树。以中值切分构造的树,每个结点是一个超矩形,在维数小于20时效率高。ball tree是为了克服kd树高纬失效而发明的,其构造过程是以质心C和半径r分割样本空间,每个节点是一个超球体。
- leaf_size:默认是30,这个是构造的kd树和ball树的大小。这个值的设置会影响树构建的速度和搜索速度,同样也影响着存储树所需的内存大小。需要根据问题的性质选择最优的大小。
- metric:用于距离度量,默认度量是minkowski,也就是p=2的欧氏距离(欧几里德度量)。
- p:距离度量公式。在上小结,我们使用欧氏距离公式进行距离度量。除此之外,还有其他的度量方法,例如曼哈顿距离。这个参数默认为2,也就是默认使用欧式距离公式进行距离度量。也可以设置为1,使用曼哈顿距离公式进行距离度量。
- metric_params:距离公式的其他关键参数,这个可以不管,使用默认的None即可。
- n_jobs:并行处理设置。默认为1,临近点搜索并行工作数。如果为-1,那么CPU的所有cores都用于并行工作。
KNeighborsClassifier提供了以一些方法供我们使用,如图3.7所示。
图3.7 KNeighborsClassifier的方法由于篇幅原因,每个函数的怎么用,就不具体讲解了。官方手册:点我查看 已经讲解的很详细了,各位可以查看这个手册进行学习,我们直接讲手写数字识别系统的实现。
5、sklearn小试牛刀
我们知道数字图片是32×32的二进制图像,为了方便计算,我们可以将32×32的二进制图像转换为1×1024的向量。对于sklearn的KNeighborsClassifier输入可以是矩阵,不用一定转换为向量,不过为了跟自己写的k-近邻算法分类器对应上,这里也做了向量化处理。然后构建kNN分类器,利用分类器做预测。创建kNN_test04.py文件,编写代码如下:
# -*- coding: UTF-8 -*-
import numpy as np
import operator
from os import listdir
from sklearn.neighbors import KNeighborsClassifier as kNN
"""
函数说明:将32x32的二进制图像转换为1x1024向量。
Parameters:
filename - 文件名
Returns:
returnVect - 返回的二进制图像的1x1024向量
Modify:
2017-07-15
"""
def img2vector(filename):
#创建1x1024零向量
returnVect = np.zeros((1, 1024))
#打开文件
fr = open(filename)
#按行读取
for i in range(32):
#读一行数据
lineStr = fr.readline()
#每一行的前32个元素依次添加到returnVect中
for j in range(32):
returnVect[0, 32*i+j] = int(lineStr[j])
#返回转换后的1x1024向量
return returnVect
"""
函数说明:手写数字分类测试
Parameters:
无
Returns:
无
Modify:
2017-07-15
"""
def handwritingClassTest():
#测试集的Labels
hwLabels = []
#返回trainingDigits目录下的文件名
trainingFileList = listdir('trainingDigits')
#返回文件夹下文件的个数
m = len(trainingFileList)
#初始化训练的Mat矩阵,测试集
trainingMat = np.zeros((m, 1024))
#从文件名中解析出训练集的类别
for i in range(m):
#获得文件的名字
fileNameStr = trainingFileList[i]
#获得分类的数字
classNumber = int(fileNameStr.split('_')[0])
#将获得的类别添加到hwLabels中
hwLabels.append(classNumber)
#将每一个文件的1x1024数据存储到trainingMat矩阵中
trainingMat[i,:] = img2vector('trainingDigits/%s' % (fileNameStr))
#构建kNN分类器
neigh = kNN(n_neighbors = 3, algorithm = 'auto')
#拟合模型, trainingMat为训练矩阵,hwLabels为对应的标签
neigh.fit(trainingMat, hwLabels)
#返回testDigits目录下的文件列表
testFileList = listdir('testDigits')
#错误检测计数
errorCount = 0.0
#测试数据的数量
mTest = len(testFileList)
#从文件中解析出测试集的类别并进行分类测试
for i in range(mTest):
#获得文件的名字
fileNameStr = testFileList[i]
#获得分类的数字
classNumber = int(fileNameStr.split('_')[0])
#获得测试集的1x1024向量,用于训练
vectorUnderTest = img2vector('testDigits/%s' % (fileNameStr))
#获得预测结果
# classifierResult = classify0(vectorUnderTest, trainingMat, hwLabels, 3)
classifierResult = neigh.predict(vectorUnderTest)
print("分类返回结果为%d\t真实结果为%d" % (classifierResult, classNumber))
if(classifierResult != classNumber):
errorCount += 1.0
print("总共错了%d个数据\n错误率为%f%%" % (errorCount, errorCount/mTest * 100))
"""
函数说明:main函数
Parameters:
无
Returns:
无
Modify:
2017-07-15
"""
if __name__ == '__main__':
handwritingClassTest()
运行上述代码,得到如图3.8所示的结果。
上述代码使用的algorithm参数是auto,更改algorithm参数为brute,使用暴力搜索,你会发现,运行时间变长了,变为10s+。更改n_neighbors参数,你会发现,不同的值,检测精度也是不同的。自己可以尝试更改这些参数的设置,加深对其函数的理解。
四、总结
1、kNN算法的优缺点
优点
- 简单好用,容易理解,精度高,理论成熟,既可以用来做分类也可以用来做回归;
- 可用于数值型数据和离散型数据;
- 训练时间复杂度为O(n);无数据输入假定;
- 对异常值不敏感
缺点
- 计算复杂性高;空间复杂性高;
- 样本不平衡问题(即有些类别的样本数量很多,而其它样本的数量很少);
- 一般数值很大的时候不用这个,计算量太大。但是单个样本又不能太少,否则容易发生误分。
- 最大的缺点是无法给出数据的内在含义。
2、其他
- 关于algorithm参数kd_tree的原理,可以查看《统计学方法 李航》书中的讲解;
- 关于距离度量的方法还有切比雪夫距离、马氏距离、巴氏距离等;
- 下篇文章将讲解决策树,欢迎各位的捧场!
- 如有问题,请留言。如有错误,还望指正,谢谢!
PS: 如果觉得本篇本章对您有所帮助,欢迎关注、评论、赞!
我为大家准备了超详细的学习资料,算法工程师的学习路线和Leetcode刷题笔记,这也是我的自学资料,希望可以帮助读者少走弯路:
参考资料:
- 本文中提到的电影类别分类、约会网站配对效果判定、手写数字识别实例和数据集,均来自于《机器学习实战》的第二章k-近邻算法。
- 本文的理论部分,参考自《统计学习方法 李航》的第三章k近邻法以及《机器学习实战》的第二章k-近邻算法。
来源:
https://cuijiahua.com/blog/2017/11/ml_1_knn.html