排序（5）：简单选择排序

一、前言

简单选择排序是一种选择排序。

选择排序：每趟从待排序的记录中选出关键字最小的记录，顺序放在已排序的记录序列末尾，直到全部排序结束为止。

二、算法思想

简单排序很简单，它的大致处理流程为：

从待排序序列中，找到关键字最小的元素；
如果最小元素不是待排序序列的第一个元素，将其和第一个元素互换；
从余下的 N – 1 个元素中，找出关键字最小的元素，重复(1)、(2)步，直到排序结束。

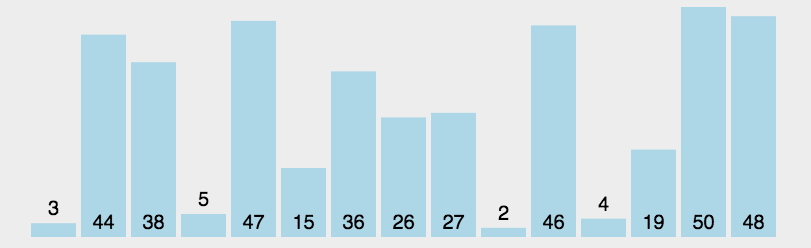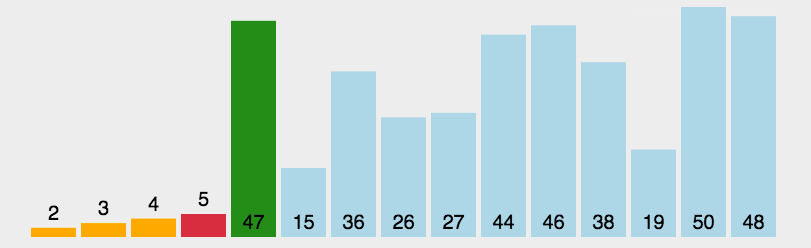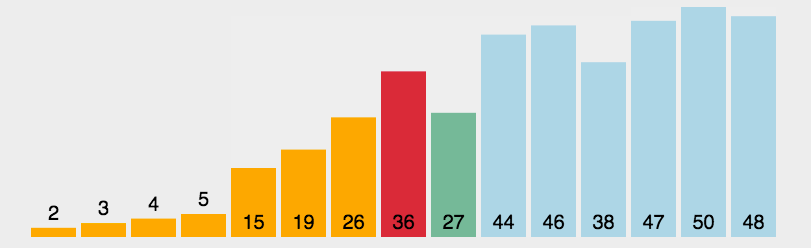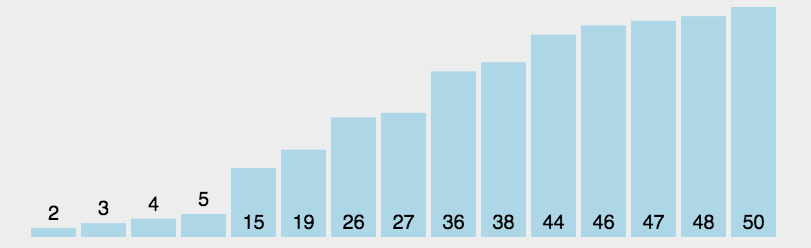
动态效果示意图：

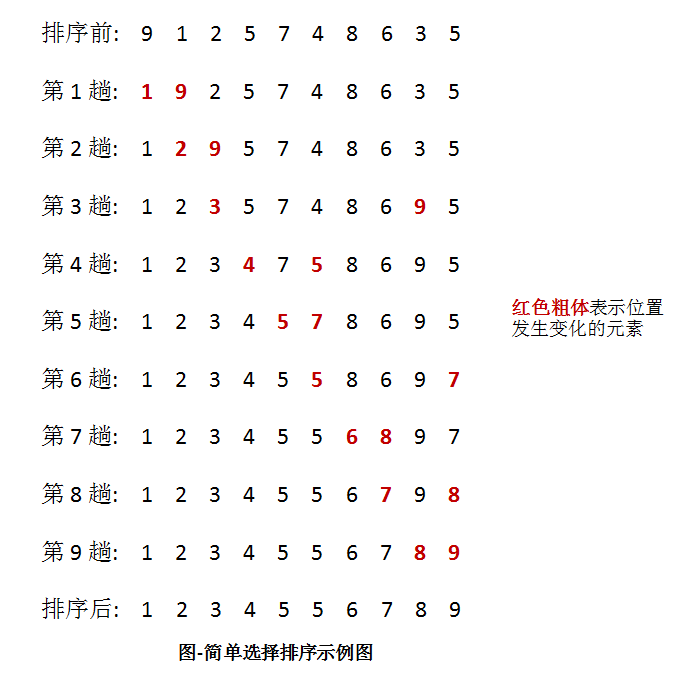
举例说明，处理过程示意图如下所示：

如图所示，每趟排序中，将当前第 i 小的元素放在位置 i 上。

1、代码

C++：

#include <iostream>
#include <vector>

using namespace std;

// 简单选择排序
vector<int> SelectSort(vector<int> list){
	// 需要遍历获得最小值的次数
	// 要注意一点，当要排序 N 个数，已经经过 N-1 次遍历后，已经是有序数列
	vector<int> result = list;
	for (int i = 0; i < result.size(); i++){
		// 用来保存最小值得索引
		int index = i;
		// 用来保存最小值得索引
		for (int j = i + 1; j < result.size(); j++){
			if (result[index] > result[j]){
				index = j;
			}
		}
		if (index == i){
			continue;
		}
		// 将找到的第i个小的数值放在第i个位置上
		swap(result[i], result[index]);
		cout << "第" << i + 1<< "趟:\t";
		for (int i = 0; i < result.size(); i++){
			cout << result[i] << " ";
		}
		cout << endl;
	}
	return result;
}

void main(){
	int arr[] = { 6, 4, 8, 9, 2, 3, 1 };
	vector<int> test(arr, arr + sizeof(arr) / sizeof(arr[0]));
	cout << "排序前" << endl;
	for (int i = 0; i < test.size(); i++){
		cout << test[i] << " ";
	}
		cout << endl;
	vector<int> result;
	result = SelectSort(test);
	cout << "排序后" << endl;
	for (int i = 0; i < result.size(); i++){
		cout << result[i] << " ";
	}
	cout << endl;

	system("pause");
}

运行结果：

Python：

# -*- coding:utf-8 -*-

def SelectSort(input_list):
	'''
	函数说明:简单选择排序（升序）
	Author:
		www.cuijiahua.com
	Parameters:
		input_list - 待排序列表
	Returns:
		sorted_list - 升序排序好的列表
	'''	
	if len(input_list) == 0:
		return []
	sorted_list = input_list
	length = len(sorted_list)
	for i in range(length):
		min_index = i
		for j in range(i + 1, length):
			if sorted_list[min_index] > sorted_list[j]:
				min_index = j
		if min_index == i:
			continue
		temp = sorted_list[i]
		sorted_list[i] = sorted_list[min_index]
		sorted_list[min_index] = temp
	return sorted_list

if __name__ == '__main__':
	input_list = [6, 4, 8, 9, 2, 3, 1]
	print('排序前:', input_list)
	sorted_list = SelectSort(input_list)
	print('排序后:', sorted_list)

运行结果同上。

三、算法分析

1、简单算法排序性能

其中，N2为N^2。

2、时间复杂度

简单选择排序的比较次数与序列的初始排序无关。假设待排序的序列有 N 个元素，则比较次数总是N (N – 1) / 2。

而移动次数与序列的初始排序有关。当序列正序时，移动次数最少，为 0.

当序列反序时，移动次数最多，为3N (N – 1) / 2。

所以，综合以上，简单排序的时间复杂度为 O(N^2)。

3、空间复杂度

简单选择排序需要占用 1 个临时空间，用于保存最小值得索引。

本站整理自：

http://www.cnblogs.com/jingmoxukong/p/4303289.html

来源：

https://cuijiahua.com/blog/2017/12/algorithm_5.html