本文概述
本文学习什么是循环学习率策略,以及它如何改进神经网络的训练。
(本教程假定读者熟悉神经网络的基础知识)
神经网络在计算机科学学会或普通社会中不再是一个普遍的短语。使它如此酷的主要原因不仅在于它正在解决的现实世界中的问题的数量, 还在于它正在解决的问题的种类。它们如何如此变化?
在认知心理学领域, 在网络安全领域, 在医疗保健领域(暂时不考虑计算机视觉, 计算机图形学, 自然语言处理等)。 。让我们命名更不常见的!几乎每个行业都从神经网络必须提供的智能和自动化中受益匪浅。
但为什么?这是一个不断出现的问题!嗯, 关于此问题的答案仍在积极研究中, 因为神经网络本质上是一个黑匣子, 而且与大脑的相似之处使这个问题更加复杂。无论如何, 回答这个问题不是本文的目的。
有一件事是肯定的!为了从神经网络获得预期结果, 必须确保的一件事是其训练。到现在, 你可能已经发现Training非常需要巨大的计算能力。没有良好的GPU和SSD, 几乎不可能训练出非常大的神经网络。现在多少很大?好吧, 足够大以在ImageNet数据集上产生良好的结果, 因为这是一个基准。
但是, 当一群来自Fast.ai的才华横溢的研究人员能够在短短18分钟之内击败Google的模型, 实现93%的准确度(也就是40美元)时, 这种训练庞大的神经网络的想法彻底被彻底改变了。
听起来不错?继续阅读!
但是, 发生这种情况的关键因素是什么?最先进的GPU?最新的TPUS?最先进的SSD?
绝对不。团队的配置非常简单, 成本仅为40美元。关键要素是使用最先进的算法来训练神经网络。在这个博客中, 伟大的研究者和教育家杰里米·霍华德(Jeremy Howard)讨论了取得这一巨大胜利的主要原因。
这是一个经典示例, 其中昂贵的硬件功能被强大的算法功能所取代。在本文中, 你将发现一种这样的技术的详细信息, 该技术可以确保以最佳的学习率对神经网络进行训练。此技术称为循环学习率(CLR)。这是莱斯利·史密斯(Leslie N.Smith)在2015年提出的。你可以在此处检查原始纸张。
但是, 当还有其他必不可少的超参数(如辍学率和激活函数)时, 为什么只覆盖学习率呢?这是因为学习率是其中最重要的一个。只是!
在这篇文章中, 你将学习:
- 快速回顾为什么需要学习率?
- 有什么技术可以为神经网络找到最合适的学习率?
- 周期性学习率简介
- 周期性学习率的内在机制
- Python案例研究
为什么需要学习率?
让我们快速回顾一下使用学习率训练神经网络的主要目的。
学习率是一个超参数, 它控制你相对于损耗梯度来调整我们网络的权重。什么?为什么渐变出现在图片中?这是因为你正在优化刚刚通过梯度下降创建的神经网络。现在, 基本上, 梯度下降的目标是找到神经网络试图优化的损失函数的最小值。看看下面的图片[摘自安德鲁·伍的Coursera的深度学习课程]:
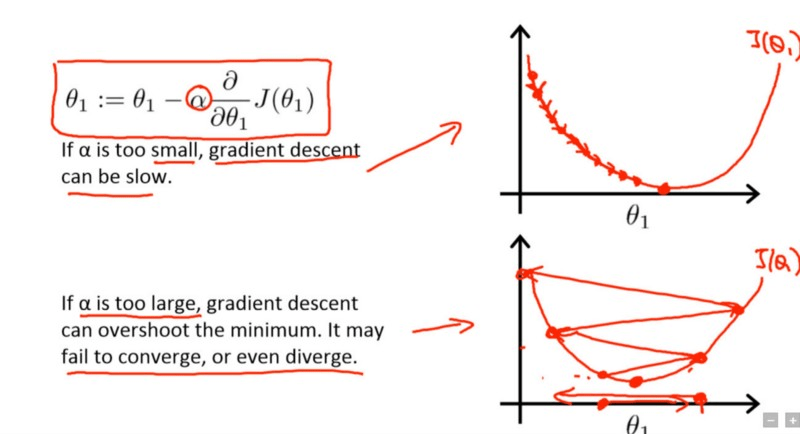
矩形中的术语是网络开始学习其参数$ \ theta $ 1的更新规则, 其中$ \ alpha $是学习速率。
在第一条曲线中, 最低点是损失函数的最小值。假设在当前迭代中, 你的网络位于最左上角附近。现在, 为了收敛最低点, 你可以使用损失函数$ J(\ theta1)$的偏导数, 并计算梯度以获得到达该最低点的方向。
为了达到更快的速度, 你添加了另一个术语$ \ alpha $, 即学习率。值越低, 沿着下坡行驶的速度越慢。尽管从确保你不会错过任何局部最小值的角度来看, 这可能是一个好主意(使用较低的学习率), 但这也可能意味着你将花费很长的时间来收敛尤其是如果你陷入困境高原地区。
这是对简单单词学习率目标的快速回顾。现在, 你将学习为神经网络选择良好的学习率的技术。
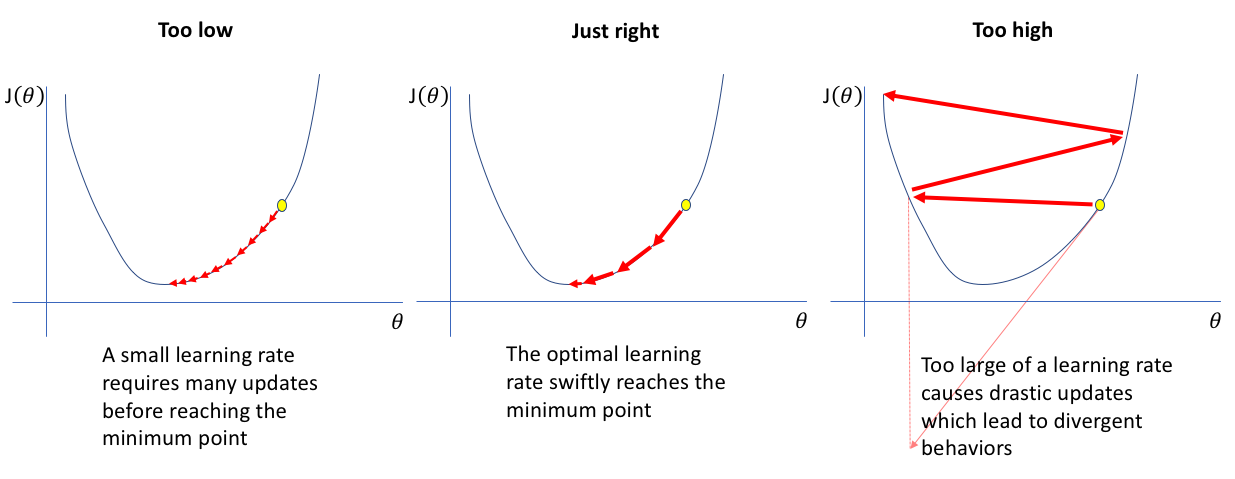
资料来源:杰里米·乔丹(Jeremy Jordan)的博客
有什么技术可以为神经网络找到最合适的学习率?
神经网络没有固定的学习率。它取决于你正在处理的问题的类型, 你要馈送到网络的数据的类型, 最重要的是取决于网络的结构, 每个问题的情况都不尽相同。手工选择学习率是一项非常痛苦的任务, 因为在培训大型网络的情况下, 你可能会承担大量的费用。而且这也是非常耗时的。
你是否应该运行诸如网格搜索或随机搜索之类的标准超参数优化方法?
- 对于大型网络而言, 这再次是可怕的。但是, 为什么你继续进入大型网络?这是因为几乎所有现实世界中的复杂问题都需要一个广泛的神经网络。
在CLR之前, 提出了自适应学习率, 可以将其视为CLR的竞争者, 但是使用自适应学习率的实验在计算上是昂贵的, 而CLR却没有。
到目前为止, 最常见的做法是将学习率设置为恒定值, 并在精度趋于稳定后将其降低一个数量级。
因此, 显然需要一种系统技术, 该技术可以简化为特定神经网络选择良好学习率的过程。不仅如此, 而且还必须有足够的理由来支持这种方法为什么值得信赖。
似乎周期性学习率(CLR)适时出现。
周期性学习率简介
周期性学习率(CLR)的目标有两个:
- CLR提供了一种为训练神经网络设置全局学习率的方法, 从而无需进行大量实验即可找到最佳值, 而无需进行额外的计算。
- CLR通过引入LR范围测试的概念, 为实验提供了出色的学习率范围(LR范围)。
你将仅学习本节内容, 以了解CLR的工作原理。在下一部分中, 你将深入研究更多细节。在前面的部分中, 你简要了解了为什么以任何方式使用学习率。让我们再次回想一下。
理想的学习率应是可以大幅降低网络损耗的学习率。这是CLR的巫术。原始CLR论文谈论的是一个实验, 你可以观察学习率相对于损失的行为。该实验可以直观地直观显示你在每次迷你批处理后逐渐提高学习率的位置, 并记录每次增量时的损失。这种逐渐增加可以是线性的也可以是指数的。是的, 这实质上是LR范围测试。
莱斯利(Leslie)向我们展示了实验之后, 由于学习率太低, 损失可能会减少, 但下降的幅度非常小。进入最佳学习率区域时, 你会发现损失函数迅速下降。如果进一步提高学习速度, 则可能导致网络中的参数丢失, 进而可能导致损耗增加。因此, 从该实验中可以很明显地看出, 你对损失函数的急剧下降很感兴趣, 为此, 你可以在训练的不同阶段分析损失函数的梯度。
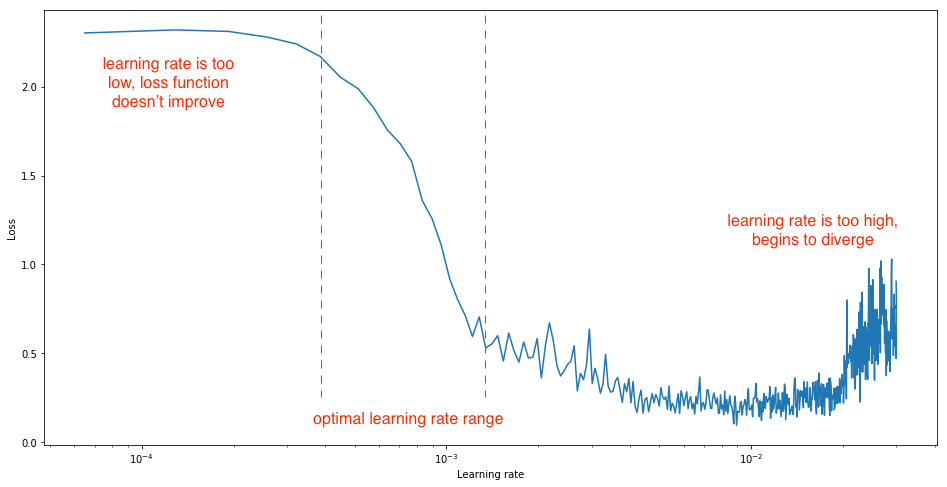
资料来源:杰里米·乔丹(Jeremy Jordan)的博客
因此, 从上面的图表中, 你可以轻松地发现损耗变化不大的三个不同阶段, 然后是出现急剧下降, 然后损耗又开始再次缓慢增长的时期。
你能看到所有其他减少中最大的减少吗?是的, 从本质上讲, 你希望最终落在该范围内, CLR将为你提供一种纪律严明的方法来找到它。了解更多信息, 让我们了解更多。
使用CLR进行更多研究
以上观察结果为你提供了重要的考虑因素:
CLR的直觉来自于让学习率在值范围内变化而不是采用线性或指数递减值的想法。你可以通过设置一定的学习率范围来做到这一点, 然后而不是进行任何线性或指数变化, 而是从定义的范围周期性地改变学习率。莱斯利(Leslie)考虑了以下函数形式来周期性地改变学习率:
- 三角窗(线性)
- 韦尔奇窗(抛物线形)
- 他窗(正弦波)
但是所有形式都产生了等效的结果, 因此, 在原始论文中, 由于其简单性, 该想法仅以三角形形式呈现(线性递增然后线性递减)。该策略也称为三角学习率策略。实现这一点也很简单。以下是三角学习率策略的一般实施:
local cycle = math.floor(1 + epochCounter / ( 2 ∗ stepsize))
local x = math.abs(epochCounter / stepsize − 2∗ cycle + 1 )
local lr = opt.LR + (maxLR − opt.LR) ∗ math.max(0 , (1−x ))
其中
- opt.LR是指定的较低(即基本)学习率,
- epochCounter是训练的纪元数,
- lr是计算出的学习率,
- 步长是周期或周期长度的一半, 并且
- max_lr是最大学习率边界
请参考以下图像, 以便直观地考虑三角形的形式:
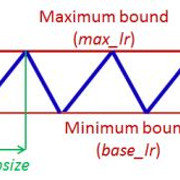
资料来源:本教程开头提到的原始CLR论文。
除了三角学习率策略外, 本文还提出了以下策略:
- 三角2-与三角策略相同, 只是在每个周期结束时将学习率差异减半。这意味着学习率差异在每个周期后都会下降。
- exp范围-在这种情况下, 学习率在最小边界和最大边界之间变化, 并且每个边界值均以指数因子下降。
你可能会在此时迅速问自己一个问题:-如何估算合理的最小和最大边界值?还记得你刚才学习的LR Range Test吗?现在, 你应该能够更好地找到其相关性。
莱斯利(Leslie)提出了一种直接简便的方法来确定学习率范围:
- 对模型运行几个时期, 同时让学习率在低学习率值和高学习率值之间线性增加(使用三角学习率策略)。
- 接下来, 绘制准确性与学习率的关系曲线。当精度开始增加, 精度降低, 变得参差不齐或开始下降时, 请注意学习率值。这两个学习率是定义学习率范围的不错选择。
现在让我们做一个快速的案例研究, 看看CLR如何产生惊人的结果。
(在本教程的最后, 你将发现最近提出的一些比CLR更高的改进, 但是到现在为止, 你已经了解了CLR的价值。)
Python CLR案例研究
你将使用经典的MNIST数据集来执行此操作, 该数据集可能是开始进入计算机视觉和深度学习的最受欢迎的数据集。如果你想非常详细地了解MNIST, 请查看此博客。你将在实验的所有目的中广泛使用keras。 keras提供了数据集的内置版本。你将通过导入实验并执行一些基本的EDA来开始实验。
from keras.datasets import mnist
Using TensorFlow backend.
你已成功导入数据集。现在, 你将对数据集进行一些基本的可视化。
import matplotlib.pyplot as plt
(X_train, y_train), (X_test, y_test) = mnist.load_data()
# Plot 4 images as gray scale
plt.subplot(152)
plt.imshow(X_train[0], cmap=plt.get_cmap('gray'))
plt.subplot(153)
plt.imshow(X_train[1], cmap=plt.get_cmap('gray'))
plt.subplot(154)
plt.imshow(X_train[2], cmap=plt.get_cmap('gray'))
plt.subplot(155)
plt.imshow(X_train[3], cmap=plt.get_cmap('gray'))
# Show the plot
plt.show()

那很棒!你将直接着手建立一个简单的多层神经网络。但是在此之前, 你将进行一些基本的数据预处理。
# Flatten 28*28 images to a 784 vector for each image
num_pixels = X_train.shape[1] * X_train.shape[2]
X_train = X_train.reshape(X_train.shape[0], num_pixels).astype('float32')
X_test = X_test.reshape(X_test.shape[0], num_pixels).astype('float32')
你做了什么?
数据集中的图像为28 * 28尺寸, 难以容纳在简单的多层神经网络中。这就是为什么你使用reshape()函数将图像转换为一个维, 其中每个图像包含784像素数据。
图像中的像素值在0-255的范围内。一个好主意是通过将范围标准化为0-1来进一步减小此值。
X_train = X_train / 255
X_test = X_test / 255
输出变量是0到9之间的整数。这是一个多类分类问题。你将对类标签执行一次热编码, 以将类整数的矢量转换为二进制矩阵。你将执行此操作以对类别进行”二值化”, 以便可以将其包括为训练神经网络的功能。
你可以使用keras中内置的np_utils.to_categorical()帮助器函数轻松地执行此操作。
from keras.utils import np_utils
y_train = np_utils.to_categorical(y_train)
y_test = np_utils.to_categorical(y_test)
num_classes = y_test.shape[1]
现在, 你将定义网络的结构。为此, 你将使用简单的完全连接的网络。在喀拉拉邦, 这通常是一个三步过程:
import numpy as np
from keras.models import Sequential
from keras.layers import Dense
# Create model
model = Sequential()
model.add(Dense(num_pixels, input_dim=num_pixels, kernel_initializer='normal', activation='relu'))
model.add(Dense(num_classes, kernel_initializer='normal', activation='softmax'))
# Compile model
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
让我们看看你在以上代码中所做的一切。你正在按顺序构造网络(这是线性的图层堆栈)。然后, 你开始在网络中添加一层, 其中第一层添加了神经元(等于图像中像素的数量, 即784), 并指定了图像的输入尺寸, 在这种情况下为与像素数相同。你指示网络使用正态分布中的权重进行初始化。最后, 你提供了relu作为第一层的激活功能。
在最后一层中, 将神经元的数量保持为10(这是类别标签的数量), 并将激活设置为softmax, 以将输出转换为类似概率的值, 并允许将10个类别中的一个作为选择作为模型的输出预测。
你可以编译模型以确定模型的优化方法(在这种情况下为ADAM)以及该方法将优化的损失类型(在这种情况下为categorical_loss)。
现在, 你将训练模型并记录训练所需的时间。你还将测试其性能。
import timeit
# For fixing the reproducibility
from numpy.random import seed
seed(1)
# Fit the model
startTime = timeit.default_timer()
model.fit(X_train, y_train, validation_data=(X_test, y_test), epochs=10, batch_size=200, verbose=2)
elapsedTime = timeit.default_timer() - startTime
print("Time taken for the Network to train : ", elapsedTime)
# Final evaluation of the model
scores = model.evaluate(X_test, y_test, verbose=0)
print("Baseline Error: %.2f%%" % (100-scores[1]*100))
Train on 60000 samples, validate on 10000 samples
Epoch 1/10
- 10s - loss: 0.2774 - acc: 0.9207 - val_loss: 0.1362 - val_acc: 0.9610
Epoch 2/10
- 8s - loss: 0.1113 - acc: 0.9675 - val_loss: 0.0951 - val_acc: 0.9720
Epoch 3/10
- 8s - loss: 0.0712 - acc: 0.9793 - val_loss: 0.0802 - val_acc: 0.9750
Epoch 4/10
- 8s - loss: 0.0503 - acc: 0.9857 - val_loss: 0.0687 - val_acc: 0.9788
Epoch 5/10
- 8s - loss: 0.0360 - acc: 0.9897 - val_loss: 0.0632 - val_acc: 0.9797
Epoch 6/10
- 8s - loss: 0.0267 - acc: 0.9928 - val_loss: 0.0643 - val_acc: 0.9784
Epoch 7/10
- 8s - loss: 0.0201 - acc: 0.9951 - val_loss: 0.0633 - val_acc: 0.9802
Epoch 8/10
- 8s - loss: 0.0150 - acc: 0.9962 - val_loss: 0.0613 - val_acc: 0.9808
Epoch 9/10
- 8s - loss: 0.0108 - acc: 0.9978 - val_loss: 0.0625 - val_acc: 0.9806
Epoch 10/10
- 8s - loss: 0.0076 - acc: 0.9988 - val_loss: 0.0612 - val_acc: 0.9809
Time taken for the Network to train : 86.4216202873591
Baseline Error: 1.91%
这个简单的模型很好地实现了大约87秒内的错误率仅为1.91%。现在你将看到CLR的强大功能。你将从克隆来自Github的CLR的keras实现开始。
成功克隆后, 应将以下文件放入本地工作目录。
CLR策略在此处作为keras回调实现。
from keras.callbacks import *
from clr_callback import *
from keras.optimizers import Adam
# You are using the triangular learning rate policy and
# base_lr (initial learning rate which is the lower boundary in the cycle) is 0.1
clr_triangular = CyclicLR(mode='triangular')
model.compile(optimizer=Adam(0.1), loss='categorical_crossentropy', metrics=['accuracy'])
在拟合网络时, 你会将clr_triangular传递给callbacks参数。这次你将使用更大的batch_size。你还将记录时间。
startTime = timeit.default_timer()
model.fit(X_train, y_train, validation_data=(X_test, y_test), epochs=10, batch_size=2000, callbacks=[clr_triangular], verbose=2)
elapsedTime = timeit.default_timer() - startTime
print("Time taken for the Network to train : ", elapsedTime)
# Final evaluation of the model
scores = model.evaluate(X_test, y_test, verbose=0)
print("Baseline Error: %.2f%%" % (100-scores[1]*100))
Train on 60000 samples, validate on 10000 samples
Epoch 1/10
- 4s - loss: 0.0046 - acc: 0.9996 - val_loss: 0.0571 - val_acc: 0.9831
Epoch 2/10
- 4s - loss: 0.0030 - acc: 0.9998 - val_loss: 0.0575 - val_acc: 0.9829
Epoch 3/10
- 4s - loss: 0.0023 - acc: 0.9999 - val_loss: 0.0594 - val_acc: 0.9827
Epoch 4/10
- 4s - loss: 0.0018 - acc: 0.9999 - val_loss: 0.0589 - val_acc: 0.9835
Epoch 5/10
- 4s - loss: 0.0014 - acc: 1.0000 - val_loss: 0.0595 - val_acc: 0.9831
Epoch 6/10
- 4s - loss: 0.0011 - acc: 1.0000 - val_loss: 0.0600 - val_acc: 0.9836
Epoch 7/10
- 4s - loss: 0.0010 - acc: 1.0000 - val_loss: 0.0612 - val_acc: 0.9832
Epoch 8/10
- 4s - loss: 8.2190e-04 - acc: 1.0000 - val_loss: 0.0621 - val_acc: 0.9829
Epoch 9/10
- 4s - loss: 6.6182e-04 - acc: 1.0000 - val_loss: 0.0624 - val_acc: 0.9836
Epoch 10/10
- 4s - loss: 5.7177e-04 - acc: 1.0000 - val_loss: 0.0635 - val_acc: 0.9836
Time taken for the Network to train : 43.23223609056981
Baseline Error: 1.64%
你能发现优势吗?这真是太神奇了!你的模型只花了44秒钟就可以接受训练, 并且产生的错误率甚至比前一个更好。很好!
恭喜你!
你已经做到了。在本教程中, 你研究了一个非常关键的问题, 即找到合适的学习率, 以及CLR如何完全改变你用来解决该问题的方式。你研究了CLR, 其中涵盖了大量细节, 并进行了一些小实验, 以了解CLR如何在更短的时间内产生一些出色的结果。
现在, 接下来呢? CLR产生的两个副产品是:
- 具有热重启的随机梯度下降也称为余弦退火
- 差异学习率
研究以上两种方法以获得对该主题的更多见解。同样, 在CLR莱斯利发表题为“神经网络超参数的纪律方法:第1部分-学习率, 批处理量, 动量和重量衰减”的论文之后, 本文再次回顾了CLR, 并讨论了选择其他重要超参数值的有效方法神经网络。 Leslie在本文中还重新介绍了他的一种称为”超级收敛”的技术。对于任何想起, 吃饭和睡觉的神经网络的人来说, 本文都是必读的。
适用范围有限是CLR的主要缺点之一。必须对其进行全面认证, 然后才能在生产级别使用它。
如果你有兴趣了解有关神经网络的更多信息, 则应该参加srcmini的Python深度学习课程, 该课程的设计非常好, 由Dan Becker(Kaggle学习主管)教授
来源:
https://www.srcmini02.com/45642.html



