GATE CS 2014考试中提出了以下问题。
1)考虑下面给出的伪代码。 DoSomething()函数将指向以leftMostChild-rightSibling表示形式表示的任意树的根作为指针的参数。树的每个节点的类型为treeNode。
typedef struct treeNode* treeptr;
struct treeNode {
treeptr leftMostChild, rightSibling;
};
int DoSomething (treeptr tree) {
int value = 0;
if (tree != NULL) {
if (tree->leftMostChild == NULL)
value = 1;
else
value = DoSomething(tree->leftMostChild);
value = value + DoSomething(tree->rightSibling);
}
return (value);
}将指向树根的指针作为DoSomething的参数传递时, 该函数返回的值对应于
(A)树中的内部节点数。
(二)树的高度。
(C)树中没有右兄弟的节点数。
(D)树中叶节点的数量。
答案:(D)
在此问题中要注意的重要事项是树的表示形式。树表示为最左侧的子级和右侧的同级窗体。因此, 如果某个节点的最左侧子节点为NULL, 则该节点没有子节点。如果我们看一下函数, 我们会注意到该函数仅对叶节点将”值”增加1。
2)假设发现了一种多项式时间算法, 该算法可以正确计算给定图中的最大集团。在这种情况下, 下列哪一项代表复杂度等级P, NP和NP Complete(NPC)的正确维恩图?
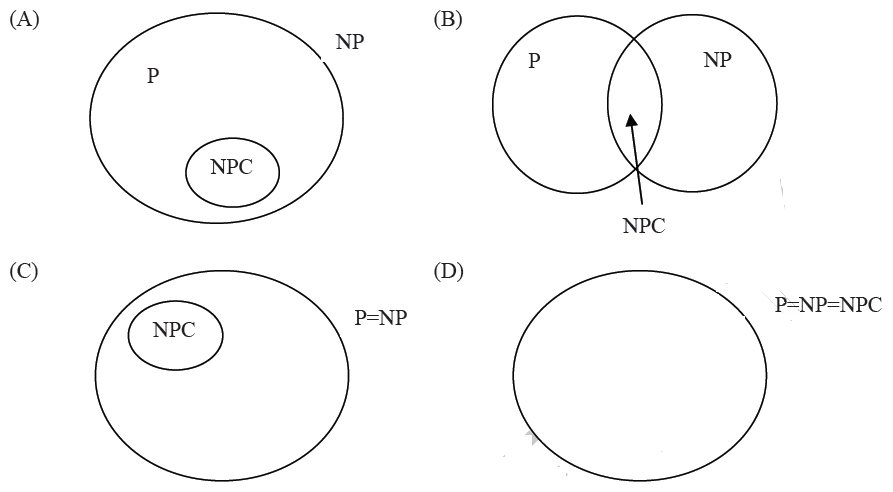
(A)A
(B)B
(C)C
(D)D
答案:(D)
最大团是一个NP完全问题。如果一个NP完全问题可以在多项式时间内解决,那么所有的NP完全问题都可以在多项式时间内解决。所以NPC集合等于P。
以下是填空题
3)找到最小和最大100个数字所需的最小比较数为____。
答案:147
n个数字所需的最小比较数为3n/2 – 3。请参考方法3
使用最少数量的比较的数组的最大值和最小值
更多细节。
4)考虑两个字符串A =” qpqrr”和B =” pqprqrp”。设x为A和B之间最长公共子序列的长度(不一定是连续的), 而y为A和B之间最长公共子序列的数目。则x + 10y = ___。
答案:34
最长为4。有3个LCS, 长度为4″ qprr”, ” pqrr”和” qpqr”。
5)假设P, Q, R, S, T是长度分别为20、24、30、35、50的排序序列。通过一次将两个序列合并在一起, 将它们合并为一个序列。在最坏的情况下, 最佳算法执行此操作所需的比较次数为____。
答案:358
要合并大小为m和n的两个列表, 在最坏的情况下我们需要进行m + n-1比较。由于我们需要一次合并2个, 因此最佳策略是首先获取最小大小的列表。选择最小的两个项目的原因是要携带最少的项目以便在合并中重复。
我们首先合并20和24, 并使用43个最坏情况的比较得出44的列表。然后, 我们使用64种最坏情况的比较将30和35合并为65的列表。然后, 我们使用93个比较将50和44合并为94的列表。最后, 我们使用158个比较合并94和65。因此比较总数为43 + 64 + 93 + 158, 即358。
如果发现任何不正确的地方, 或者想分享有关上述主题的更多信息, 请发表评论。
来源:
https://www.srcmini02.com/69086.html




