泊松过程是概率论中最重要且应用最广泛的过程之一。它广泛用于对时间或空间中的随机点建模。在本文中, 我们将简要讨论同构泊松过程。
泊松过程–
在这里, 我们将泊松过程推导为计数过程。让我们假设我们正在观察特定时间段内特定事件的发生次数。 (这里我们以时间为例。我们也可能考虑空间等。)只要它们满足以下条件, 我们就可以认为它们是在泊松过程中发生的。
- 不相交的时间间隔内的出现次数是独立的。
- 在较小的时间间隔内单次出现的概率与时间间隔的长度成正比。
- 在一个很小的时间间隔内发生多次以上的可能性可以忽略不计。
如果我们将长度为t的时间间隔内的出现次数表示为X(t), 则
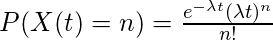
例子 –
可以使用泊松过程对许多现实情况进行建模。假设我们考虑了道路上的事故数量。我们很容易理解, 以上三个条件均已满足。对于两个不相交的时间间隔, 给定道路上的事故数量是独立的, 再次不可能在很小的时间间隔内发生两个或多个事故。凭直觉, 我们还可以假设在很小的时间间隔内发生事故的概率与时间间隔的长度成正比。一个地方的地震次数也可以使用泊松过程进行建模。
推导–
现在我们证明我们的主张, 如果X(t)是长度为t的间隔中的出现次数, 则
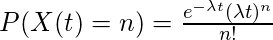
其中
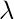
是发生率。
我们将使用数学归纳法来证明该陈述。首先, 我们用数学术语写上面写的假设。根据假设3在很小的时间间隔h
其中
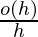
趋于零, 而h趋于零或
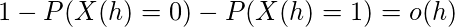
再来一次
是发生率, 然后根据假设2得出,
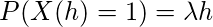
让我们取一个间隔(0, t)和一个小间隔(t, t + h)。我们将P(X(t)= n)表示为
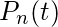
。所以上面的等式可以写成
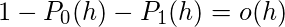
or
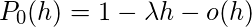
所以我们必须证明
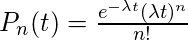
首先, 我们将证明n = 0和n = 1的结果。然后我们将证明, 如果对于n = m而言结果为true, 那么对于n = m + 1而言则为true。
取时间间隔(0, t + h)。现在,
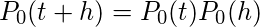
(由于间隔(0, t)和(t, t + h)中的出现是独立的)或
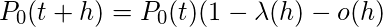
or
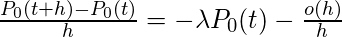
当h趋于零时取极限, 我们得到,
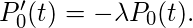
上述微分方程的解为
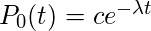
,
处于初始状态
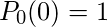
我们评估c = 0。因此,
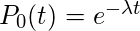
, 因此我们的主张对n = 0成立。
现在我们尝试证明n = 1。
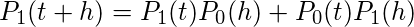
(我们使用这样的事实, 即出现的时间间隔必须是(0, t)和(t, t + h)中的一个), 或者
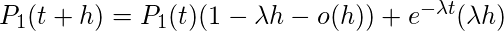
,
or
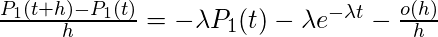
当h趋于零时再次取极限,
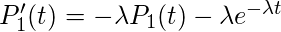
这是一阶线性微分方程, 解是
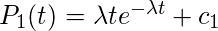
其中
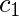
是一个常数。以来,
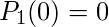
。我们得到
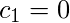
。因此
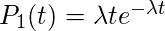
, 要么
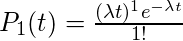
因此, 对于n = 1, 我们的说法是正确的。我们假设对于n = m, 我们的主张是正确的。
我们将证明对于n = m + 1是正确的。所以,
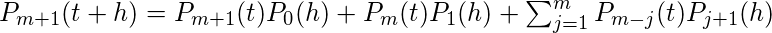
,
(我们假设m + 1发生可以不同的方式发生, 例如(0, t)中出现m + 1次, 而(t, t + h)中没有发生, 或(0, t)和1中出现m次。在(t, t + h)中出现(j, 1到m)中出现mj(0, t)中, 出现j + 1(t, t + h)中。所以,
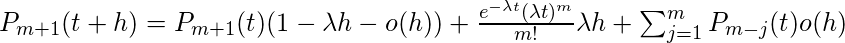
以来,
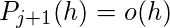
对于j> = 1。
要么,
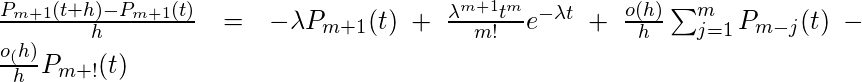
当h变为零时取极限,
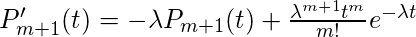
这又是一阶微分方程, 其解如此,
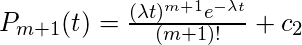
如果e假设
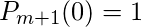
我们得到
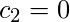
所以最终结果是
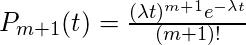
因此证明了结果。
因此, 我们得出了no的pmf。泊松过程中出现的次数, 泊松过程是具有参数的泊松分布
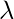
。现在如果
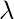
是时间的函数, 我们称此过程为
非均匀泊松过程




