活动选择问题是数学优化问题。我们的第一个例子是在几个挑战活动之间安排资源的问题。我们发现, 贪心算法为选择最大规模的手动兼容活动提供了一种精心设计且简单的方法。
假设S = {1, 2 …. n}是n个提议活动的集合。这些活动共享一次只能由一个活动使用的资源, 例如, 网球场, 演讲厅等。每个活动“ i”具有开始时间si和结束时间fi, 其中si≤fi。如果选择的活动“ i”同时发生在半开放时间间隔[si, fi)中。如果间隔(si, fi)和[si, fi)不重叠, 则活动i和j是兼容的(即, 如果si≥fi或si≥fi, 则i和j是兼容的)。活动选择问题选择了相互一致活动的最大大小集。
贪婪算法-活动选择器
GREEDY- ACTIVITY SELECTOR (s, f)
1. n ← length [s]
2. A ← {1}
3. j ← 1.
4. for i ← 2 to n
5. do if si ≥ fi
6. then A ← A ∪ {i}
7. j ← i
8. return A示例:给定10个活动及其开始时间和结束时间
S = (A1 A2 A3 A4 A5 A6 A7 A8 A9 A10)
Si = (1, 2, 3, 4, 7, 8, 9, 9, 11, 12)
fi = (3, 5, 4, 7, 10, 9, 11, 13, 12, 14)计算一个计划, 其中进行最大数量的活动。
解决方案:使用贪婪策略解决上述活动计划问题的方法如下所示:
按结束时间的升序安排活动

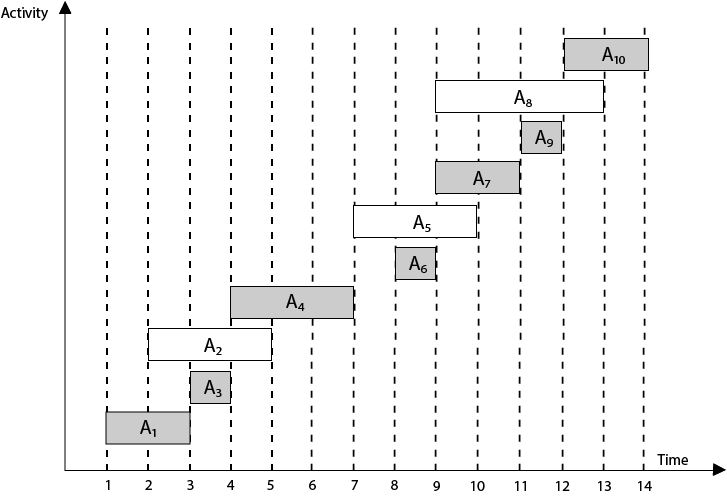
现在, 安排A1
作为A1和A3的下一个时间表A3是无干扰的。
下一步跳过A2, 因为它有干扰。
接下来, 由于A1 A3和A4不干扰, 所以调度A4, 然后, 因为A1 A3 A4和A6不干扰, 所以接下来, 调度A6。
跳过A5干扰一下。
接下来, 由于A1 A3 A4 A6和A7是互不干扰的, 所以时间表A7。
接下来, 由于A1 A3 A4 A6 A7和A9是互不干扰的, 所以时间表A9是不干扰的。
跳过A8会造成干扰。
接下来, 由于A1 A3 A4 A6 A7 A9和A10是互不干扰的, 所以调度A10。
因此, 最终的活动计划为:





